1.卷积神经网络中的相关计算问题
(1)单纯的二维卷积
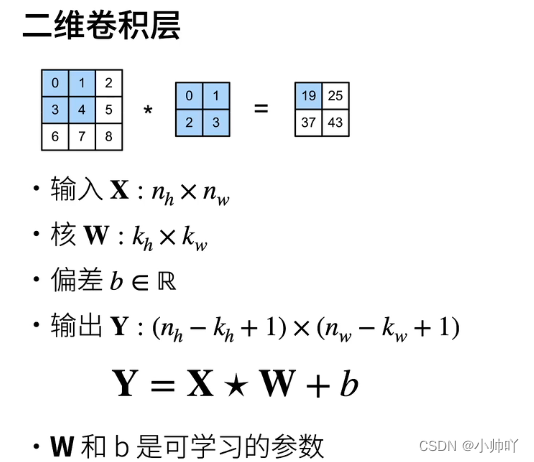
(2)加入填充(padding)
注:下图中的ph为在代码中设置的padding值的二倍
(3)加入填充(padding)和步幅(stride)

卷积核和过滤器(fliter)是有区别的,卷积核是二维概念,过滤器由一个或者多个卷积核拼成。
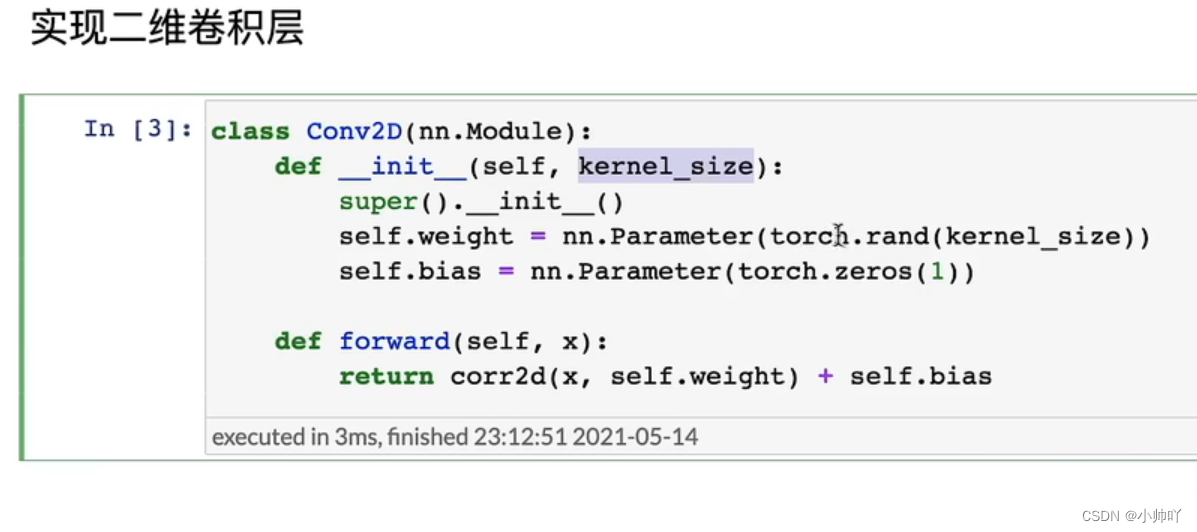
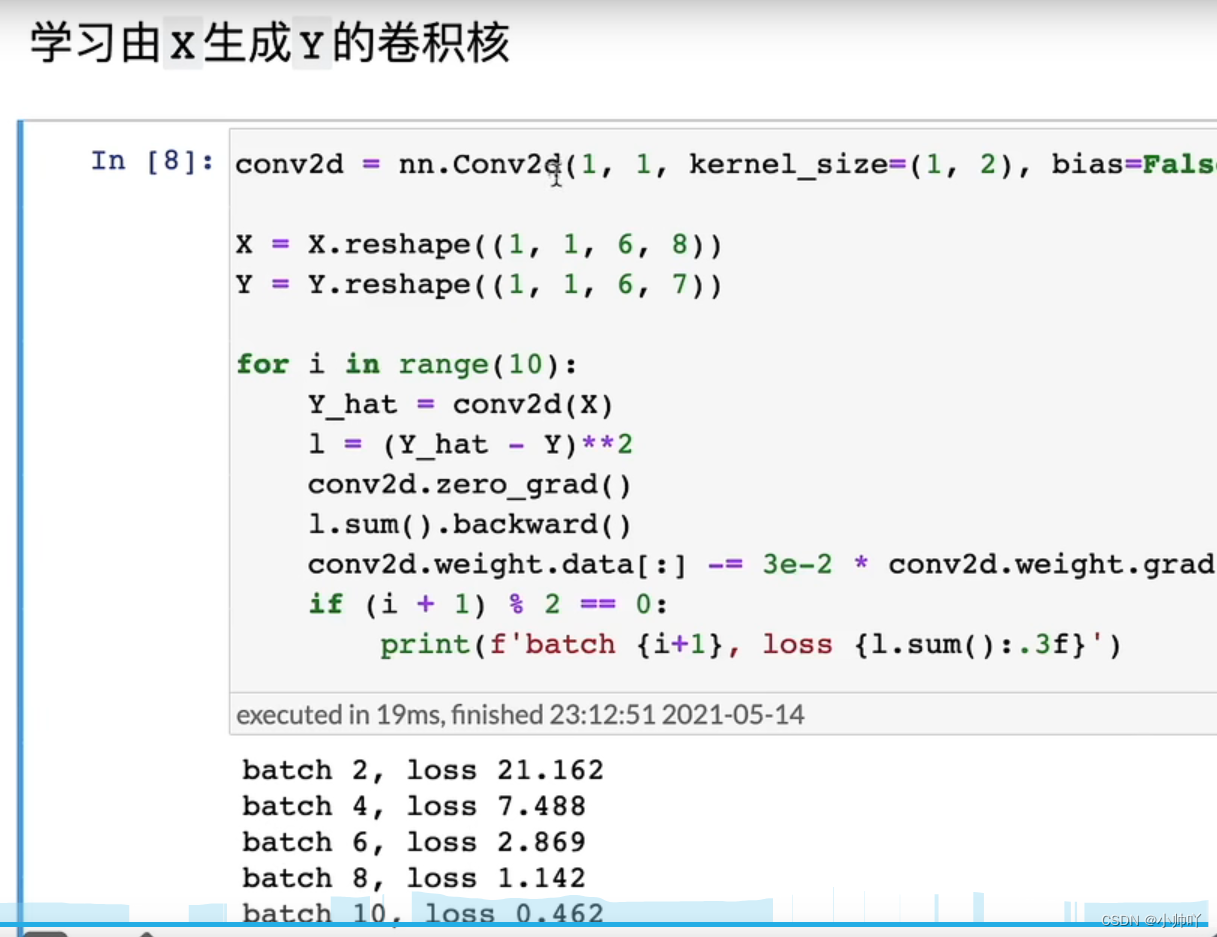
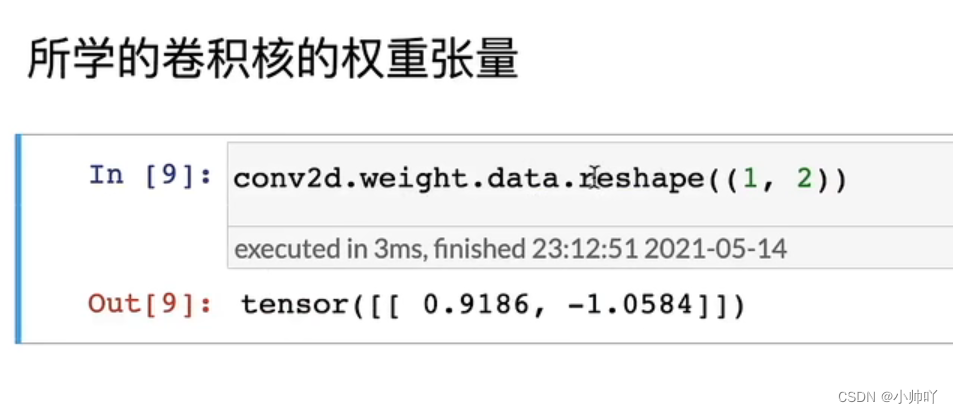
2.通过一个实例学习卷积神经网络的构建
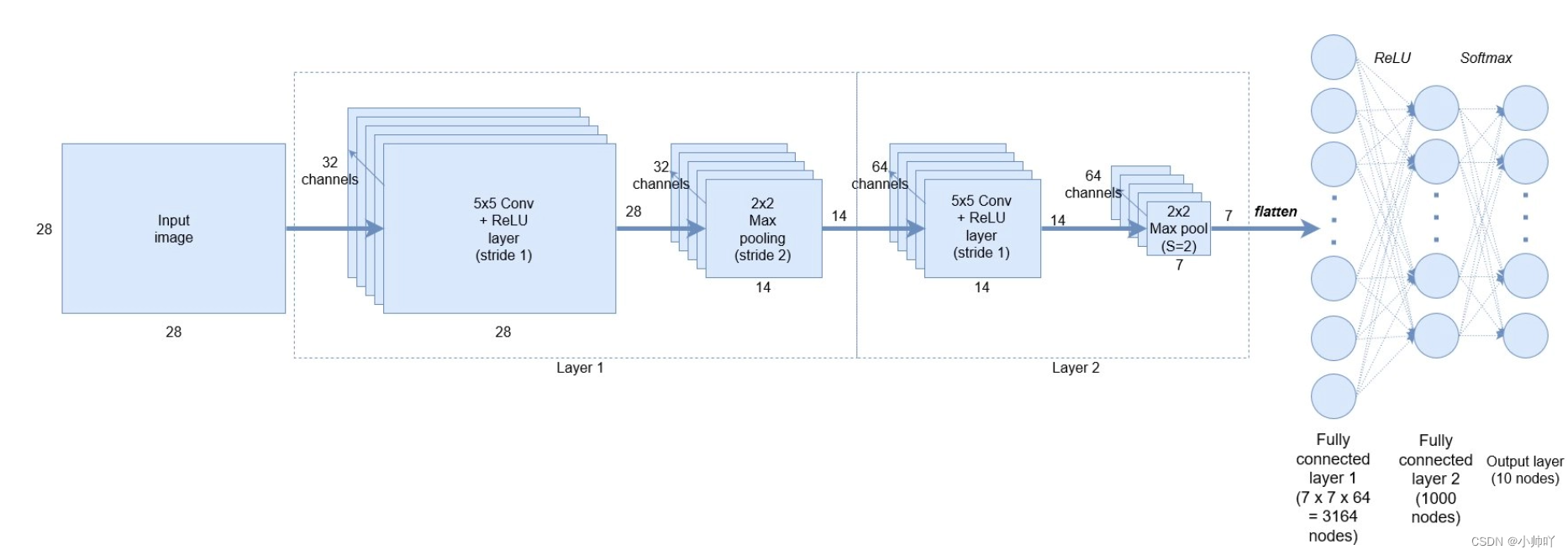
通过以下代码构建上图的神经网络
class ConvNet(nn.Module):
def __init__(self):
super(ConvNet, self).__init__()
self.layer1 = nn.Sequential(
nn.Conv2d(1, 32, kernel_size=5, stride=1, padding=2),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2))
self.layer2 = nn.Sequential(
nn.Conv2d(32, 64, kernel_size=5, stride=1, padding=2),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2))
self.drop_out = nn.Dropout()
self.fc1 = nn.Linear(7 * 7 * 64, 1000)
self.fc2 = nn.Linear(1000, 10)
def forward(self, x):
out = self.layer1(x)
out = self.layer2(out)
out = out.reshape(out.size(0), -1)
out = self.drop_out(out)
out = self.fc1(out)
out = self.fc2(out)
return out
3.卷积神经网络相关内容



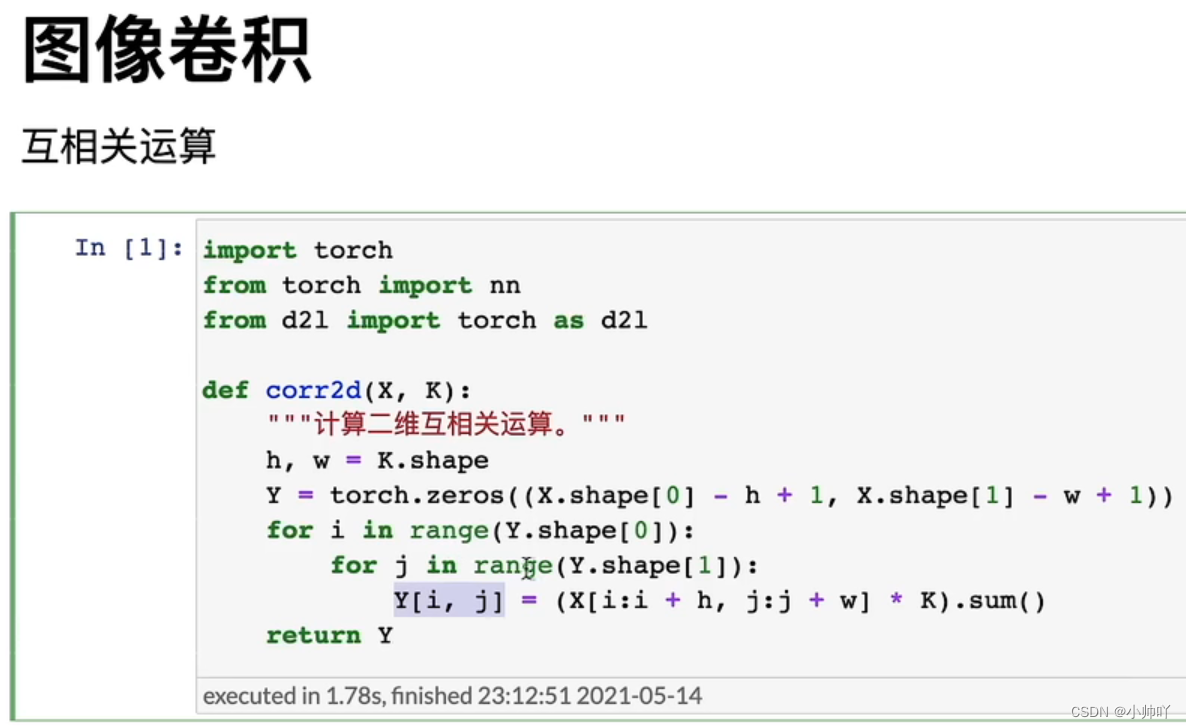
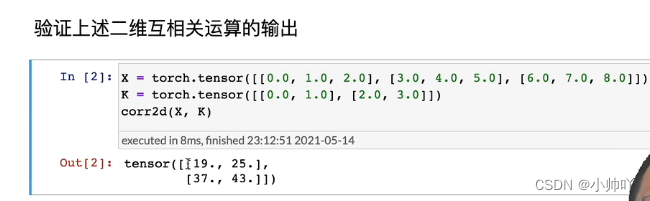
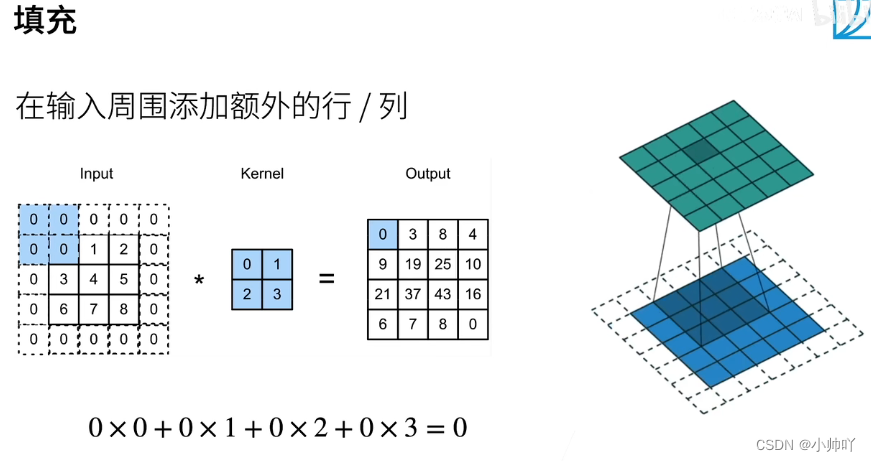
卷积层里的填充和步幅
当卷积核比较大或者经过多次卷积后图像的过小此时考虑通过填充操作来缓解

当输入图片大小比较大时,在小的卷积核下要经过很多层计算才能实现
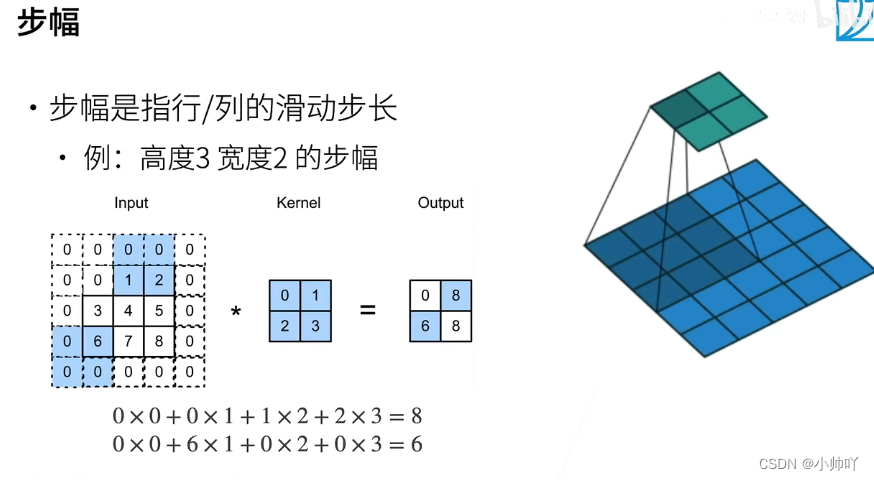


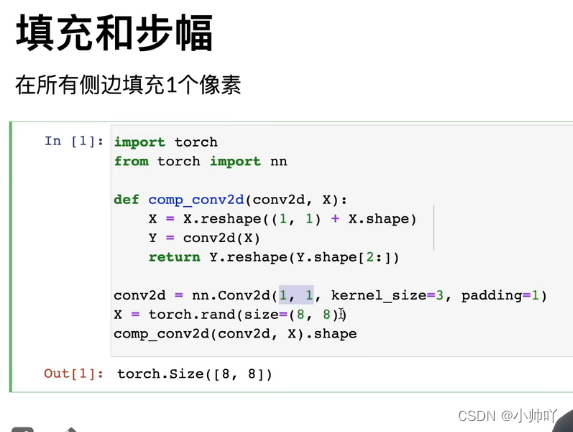
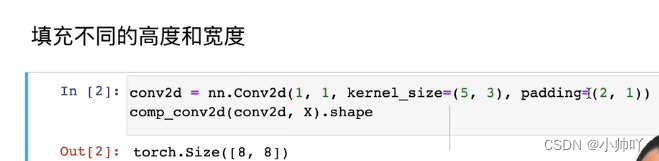
8-5+1+4=8
8-3+1+2=8
8 / 2 = 4
(8-3+0+3)/3=2
(8-5+2+4)/4=2
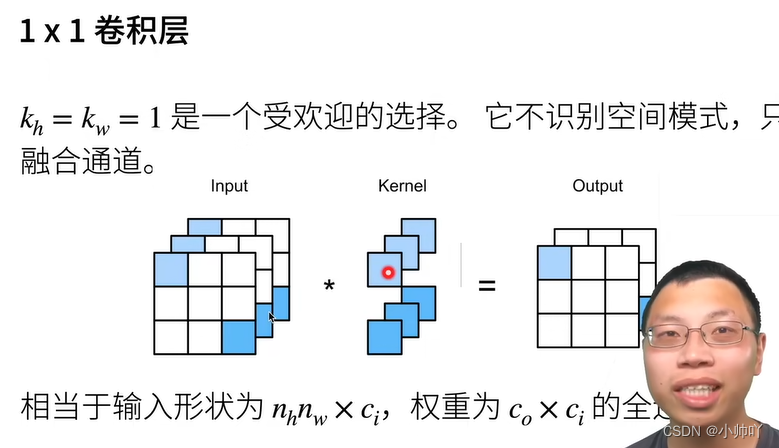
卷积层里的多输入多输出通道
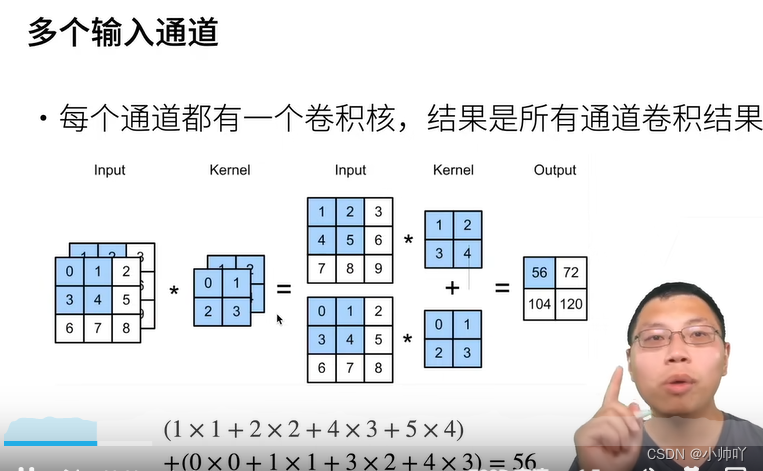





版权声明:本文为qq_47997583原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。