SMOOTHING (LOWPASS) SPATIAL FILTERS

Gonzalez R. C. and Woods R. E. Digital Image Processing (Forth Edition).

import cv2
import matplotlib.pyplot as plt
import numpy as np

FILTERS

filters实际上就是通过一些特殊的kernel $w$ 对图片进行如下操作:
$$g(x,y)=\sum _{s=-a}^a\sum _{t=-b}^{b}w(s,t)f(x+s,y+t),x=1,2,\cdots ,M,y=1,2,\cdots N.$$
其中$w(s,t)\in {\mathbb{R}}^{m\times n},m=2a+1,n=2b+1$.

注: 一般来说kernel的边是奇数, 这样可以确定唯一的中心, 但是偶数其实也是可以的.

实际上, 上面可以转换成卷积的形式:
$$(w\ast f)(x,y)=\sum _{s=-a}^a\sum _{t=-b}^b{w}^{\prime }(s,t)f(x-s,y-t),x=1,2,\cdots ,M,y=1,2,\cdots N.$$
只是$w^{\prime }(s,t)=w(-s,-t)$, 不过下面我们仅考虑卷积操作, 故直接定义为:
$$(w\ast f)(x,y)=\sum _{s=-a}^a\sum _{t=-b}^{b}w(s,t)f(x-s,y-t),x=1,2,\cdots ,M,y=1,2,\cdots N.$$
即可.

注: 注意到上面会出现$f(-1,-1)$之类的未定义情况, 常见的处理方式是在图片周围加padding(分别为pad a, b), 比如补0或者镜像补.

用卷积的目的是其特别的性质:

1. $f\ast g=g\ast f$;
2. $f\ast (g\ast h)=(f\ast g)\ast h$;
3. $f\ast (g+h)=(f\ast g)+(g\ast h)$.

注: $f,g,h$应当形状一致.

特别的, 如果
$$w=u{v}^T,$$
则
$$w\ast f=u^{\prime }\ast (v^T\ast f),u^{\prime }(x)=u(-x).$$
可以显著降低计算量.

Box Filter Kernels

即
$$w_{ij}=\frac{1}{mn},i=1,2,\cdots ,m,j=1,2,\cdots ,n.$$

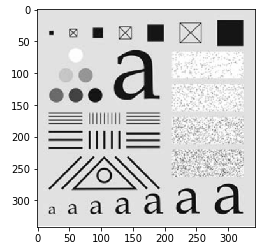
img = cv2.imread("./pics/alphabeta.png")
img.shape

img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # 由于是截图, 先转成灰度图
plt.imshow(img, cmap='gray')

# 或者等价地用 cv2.blur(img, (m, n))
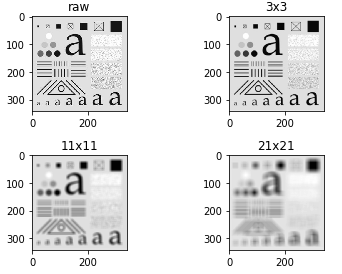
kernels = [np.ones((i, i)) / (i * i) for i in [3, 11, 21]]
imgs_smoothed = [cv2.filter2D(img, -1, kernel) for kernel in kernels]
fig, axes = plt.subplots(2, 2)
axes[0, 0].imshow(img, cmap='gray')
axes[0, 0].set_title("raw")
axes[0, 1].imshow(imgs_smoothed[0], cmap="gray")
axes[0, 1].set_title("3x3")
axes[1, 0].imshow(imgs_smoothed[1], cmap="gray")
axes[1, 0].set_title("11x11")
axes[1, 1].imshow(imgs_smoothed[2], cmap="gray")
axes[1, 1].set_title("21x21")
plt.tight_layout()
plt.show()

Lowpass Gaussian Filter Kernels

即
$$w(s,t)=G(s,t)=K{e}^{-\frac{s^2+t^2}{2{\sigma }^2}},$$
高斯分布的特点是绝大部分集中于$(-3\sigma ,+3\sigma )$之间, 故一般$w$的大小选择为$(-6\sigma ,+6\sigma )$, 需要注意的是, $\sigma$的选择和图片的大小息息相关.

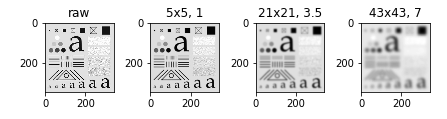
imgs_smoothed = [cv2.GaussianBlur(img, ksize=ksize, sigmaX=sigma) for (ksize, sigma) in [((5, 5), 1), ((21, 21), 3.5), ((43, 43), 7)]]
fig, axes = plt.subplots(1, 4)
axes[0].imshow(img, cmap='gray')
axes[0].set_title("raw")
axes[1].imshow(imgs_smoothed[0], cmap="gray")
axes[1].set_title("5x5, 1")
axes[2].imshow(imgs_smoothed[1], cmap="gray")
axes[2].set_title("21x21, 3.5")
axes[3].imshow(imgs_smoothed[2], cmap="gray")
axes[3].set_title("43x43, 7")
plt.tight_layout()
plt.show()

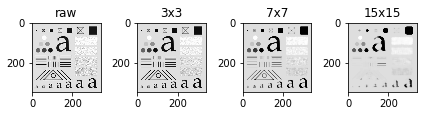
Order-Statistic (Nonlinear) Filters

即$g(x,y)$由$(x,y)$周围的点的一个某个顺序的值代替, 比如median.

imgs_smoothed = [cv2.medianBlur(img, ksize=ksize) for ksize in [3, 7, 15]]
fig, axes = plt.subplots(1, 4)
axes[0].imshow(img, cmap='gray')
axes[0].set_title("raw")
axes[1].imshow(imgs_smoothed[0], cmap="gray")
axes[1].set_title("3x3")
axes[2].imshow(imgs_smoothed[1], cmap="gray")
axes[2].set_title("7x7")
axes[3].imshow(imgs_smoothed[2], cmap="gray")
axes[3].set_title("15x15")
plt.tight_layout()
plt.show()