单点平均多点平均及累加平均算法（CMA）滑窗算法的python实现

1. 滑窗算法

通过给定窗口尺寸大小和滑窗步长，来计算窗口内序列数值的均值，对数据进行平滑处理。

2. CMA算法

累加平均算法
CMA算法数学解释

2.1 单点滑窗与多点滑窗

方案1：

方案2：

方案3：

滑窗计算公式，参考文献《东北电网风电惯量及一次调频实测与分析》

3. python代码实现

# -*- coding: utf-8 -*-
"""
Created on Tue Jun 21 15:50:51 2022
@author: HP
实现文献《东北电网风电惯量及一次调频实测与分析》中，
章节3.1中的滑动平均的计算，及CMA算法的实现
"""
import numpy as np
from matplotlib import pyplot as plt
from scipy.interpolate import make_interp_spline
import pandas as pd

def opendata(filename):
    '''
    opendata:打开文件夹
    filename:文件夹名称
    返回csv文件内制定标签所对应的数据
    '''
    data=pd.read_csv(filename,encoding='gbk')
    x=data['time_tag']
    y= data['frequency']
    return x,y

def single_point(x,y,point,s_times):
    '''
    单点采样平均
    x,y：处理的序列数据
    point：单点采样间隔步长
    s_times：滑窗时间，单位s
    p：返回单点平均变化率曲线图
    '''
    dfdt=np.zeros(len(y)+point)
    for i in range(0,len(y)-point):
        dfdt[i+point]=(y[i+point]-y[i])/s_times
    p=plt.plot(x[point:],dfdt[point:-point],label='single_point')
    return p

def multi_point(x,y,point,s_times,strides):
    '''
    多点采样平均，窗口移动步长为point
    x,y：处理的序列数据
    point：多点采样个数
    s_times：滑窗时间，单位s
    strides：窗口移动步长
    p：返回多点平均变化率曲线图
    '''
    dfdt=np.zeros(len(y)+1)
    sum1=np.zeros(len(y)+1)
    ave=np.zeros(len(y)+1)
    for i in range(0,len(y)-point+1):
        for j in range(point):
            sum1[i]=sum1[i]+y[j+i]
            ave[i]=sum1[i]/point
        dfdt[i]=(sum1[i]-sum1[i-strides])/point
    p=plt.plot(x[2*strides-1:],dfdt[strides:-strides],'-',label='multi_point')
    
    return p

def f(x,y):
    '''
    频率变化率计算
    x,y：处理的序列数据
    dfdt：返回频率变化率序列
    '''
    dfdt=np.zeros(len(y))
    for i in range(len(y)-1):
        dfdt[i+1]=(y[i+1]-y[i])/(x[i+1]-x[i])
    return dfdt

def CMA(x,y):
    '''
    累计移动平均变化率计算
    x,y：处理的序列数据
    p：返回累加平均变化率变化图
    '''
    Cma=np.zeros(len(y))
    cma=np.zeros(len(y))
    dfdt=f(x,y)
    for j in range(1,len(y)):
        Cma[j]=Cma[j-1]+dfdt[j]
        cma[j]=Cma[j]/(j+1)
    p=plt.plot(x,cma,label='CMA')
    plt.legend()
    return p

if __name__ == "__main__":
    filename1='D:\yourfilename.csv'
    x=opendata(filename1)[0]
    y=opendata(filename1)[1]
    dfdt=f(x,y)
    plt.plot(x,dfdt,'-',label='dfdt')
    y_single=single_point(x,y,9,0.2)
    y_multi=multi_point(x,y,10,0.2,10)
    y_multi_1=multi_point(x,y,5,0.02,1)
    y_CMA=CMA(x,y)

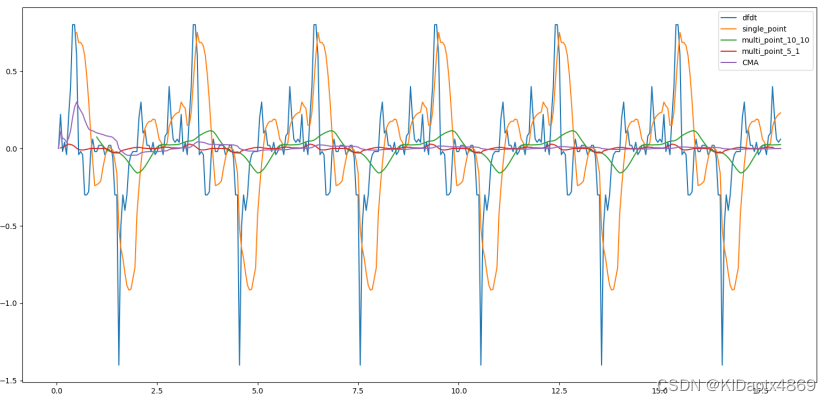
4. 运行结果