中国MOOC大学_数据结构与算法实战_周强_辛酸解题二

P10 推断学生所属学校的人数 (15 分)
某个比赛现场有来自不同学校的N名学生，给出M对“两人同属一所学校”的关系， 请推断学校数量，并找出人数最多的学校。

输入格式:
第一行是一个在[2, 1000]范围的整数N，

接下来N行，每行是一个在现场的学生的姓名，每个姓名仅由字母组成，长度不超过30。

接下来一行是非负整数M，表示有M对关系；

然后是M行，每行是用空格间隔的两个人名，表示同属一所学校。

输出格式:
在一行内分别输出学校的数量以及人数最多学校的人数，用一个空格分隔。

输入样例:

8
Bill
Ellen
Ann
Chris
Daisy
Flin
Henry
Grace
5
Ann Chris
Ellen Chris
Daisy Flin
Henry Ellen
Grace Flin

输出样例:

3 4

上代码
并查集基本查找的题

#include <iostream>
#include <queue>
#include <set>
#include <map>
using namespace std;
template<class T>
struct DisjointSet{
    int *parent;
    T *data;
    set<T> *mates;
    int capacity;
    int size;
    map<T,int> m;
    DisjointSet(int max=10){
        capacity = max;
        size = 0;
        parent = new int[max+1];
        data = new T[max+1];
        mates = new set<T>[max+1];
    }
    ~DisjointSet(){
        delete [] parent;
        delete [] data;
    }
    bool insert(T x){
        if(size==capacity)return false;

         data[++size]=x;
         parent[size]=-1;
         mates[size].insert(x);
         m[x]=size;
         return true;
    }
    int find(T x){
        typename map<T,int>::iterator it;
        it = m.find(x);
        if(it == m.end())return -1;
        int rt,i;
        i=rt = it->second;
       while(parent[rt]>0)
           rt= parent[rt];
       int tmp;
       for(;i!=rt;i=tmp)
       {
           tmp = parent[i];
           parent[i] = rt;
       }
        return rt;

    }
    void unionSet(T x,T y){
        int rx,ry;
        rx = find(x);
        ry = find(y);
        if(rx==-1 || ry ==-1)return;
        if(rx == ry)return;
        if(parent[rx]<parent[ry]){
            parent[rx] +=parent[ry];
            parent[ry] = rx;
            mates[rx].insert(mates[ry].begin(),mates[ry].end());
            mates[ry].clear();
        }
        else{
            parent[ry] +=parent[rx];
            parent[rx]=ry;
            mates[ry].insert(mates[rx].begin(),mates[rx].end());
            mates[rx].clear();
        }

    }
//    void test(){
//        unionSet(1,3);
//        unionSet(2,4);
//        print();
//    }

    void print(){
        for(int i=1;i<=size;i++)
            cout << i <<"\t";
        cout <<endl;
        for(int i=1;i<=size;i++)
            cout << parent[i] <<"\t";
        cout <<endl;
        for(int i=1;i<=size;i++)
            cout << data[i] <<"\t";
        cout <<endl;
    }
};


int main(){
    int M,N;
    cin >> N;
    DisjointSet<string> s(N);
    string name;
    for(int i=0;i<N;i++)
    {
        cin >> name;
        s.insert(name);
    }
    cin >>M;
    string name2;
    for(int i=0;i<M;i++){
        cin >> name >> name2;
        s.unionSet(name,name2);
    }
    int maxid=0,maxsize=0,numOfSchools = 0;
    for(int i=1;i<=N;i++){
        if(s.mates[i].size()>0) numOfSchools++;
        if(s.parent[i] < maxsize){

            maxsize = s.parent[i];
            maxid = i;
        }

    }
    cout << numOfSchools <<' '<<-maxsize<< endl;  //打印学校的数量

    return 0;
}

P11 堆的操作 (15 分)
编写代码，实现最小堆（Min-Heap）的操作。

输入格式:
第一行是两个不大于1000的正整数N和K，用空格间隔。其中N是堆的容量，需创建一个容量为N的堆。

接下来K行，是对这个堆的依次的K项插入或删除操作：用 1 x 表示插入元素x；用 -1 表示删除堆顶。

接下来一行是一个不大于1000的正整数M，

接下来一行是M个整数（在整型范围内），用空格间隔，

要求将这M个整数组成的列表调整为一个最小堆。

输出格式:
对于第一个堆的K项操作，每次操作后，在一行中依次序打印堆元素，元素间使用1个空格分隔；

对于第二个堆，在调整完成后，在一行中依次序打印堆元素，元素间使用1个空格分隔。

输入样例:

10 8
1 1
1 2
1 3
1 4
1 5
-1
1 6
-1
8
1 2 3 4 5 6 7 8

输出样例:

1
1 2
1 2 3
1 2 3 4
1 2 3 4 5
2 4 3 5
2 4 3 5 6
3 4 6 5
1 2 3 4 5 6 7 8

代码：
最小堆的建立
从数组中自己建立最小堆的过程，可以把时间复杂度降到O(logN)

#include <iostream>
#include <stdio.h>
#include <stdlib.h>

typedef int Elem;

struct heap{
    Elem *data;
    int capacity; 
    int size; //当前队列容量
};

using namespace std;

typedef struct heap* Heap; 
Heap initHeap(int max){
    Heap h;
     h = (Heap)malloc(sizeof(struct heap));
     if(!h)return NULL;
     h->data = (Elem*) malloc(sizeof(Elem)*(max +1));
     if(!h->data)return NULL;
     h->capacity = max;
     h->size = 0;
     return h;

}
void destroy(Heap h)
{
    if(h->data)free(h->data);
    if(h)free(h);
}

void printHeap(Heap h){
    if(h){
        for(int i=1;i<=h->size;i++)
            if(i==1)printf("%d",h->data[i]);//C语言有局限性
            else printf(" %d",h->data[i]);
        putchar('\n');
    }
}
int isEmpty(Heap h)
{
    return h->size==0;
}

int isFull(Heap h){
    return h->capacity == h->size; //判断满
}
void percolateUp(int k,Heap h){
    Elem x;
    x = h->data[k];
    int i;
    for( i=k;i>1 && x<h->data[i/2];i /= 2 )//最小堆 用x比较
    {
        h->data[i] = h->data[i/2];
    }
    h->data[i] = x ;
}
void percolateDown(int k,Heap h){
    Elem x;
    x = h->data[k];
    int i,child;
    for(i=k;i*2<=h->size;i=child){
        child = i*2;
        if(child != h->size && h->data[child]> h->data[child +1])child++;
        if(x > h->data[child])h->data[i]= h->data[child];      //跟最小的比，如果不是最小，儿子上移
        else break;
    }
    h->data[i]=x;
}

// 插入堆
int insertHeap(Elem x,Heap h){
    if(isFull(h))return 0;
    h->data[++h->size]  = x; //在数组最后一个位置插入
    percolateUp(h->size, h);//向上过滤
    return 1;
}
//删除堆元素
int removeHeap(Elem *px,Heap h){
    if(isEmpty(h))return 0;
    *px = h->data[1]; //取堆顶元素
    h->data[1] = h->data[h->size--];
    percolateDown(1,h);
    return 1;
}
Heap buildHeap(Elem *a,int size,int max){
    Heap h= initHeap(max);
    if(!h)return NULL;
    h->size = size;
    for(int i=1;i<=size;i++)
        h->data[i] = a[i-1];
    for(int i=size/2;i>0;i--){
        percolateDown(i,h);
    }
    return h;
}

int main()
{
    int N,K,M;
    cin >>N>>K;
    Heap h;
    h = initHeap(N);
    int flag,tem;
    for(int i=0;i<K;i++){
        cin>>flag;
        if(1==flag){
            cin >> tem;
            insertHeap(tem,h);

        }
        else if(-1 ==flag)
        {
            removeHeap(&tem,h);
        }
        printHeap(h);
    }
    cin >>M;
    int a[M];
    for(int i=0;i<M;i++)cin>>a[i];
    Heap h2 = buildHeap(a,M,1000);
    printHeap(h2);

    return 0;
}

P12 两点间有路径吗？ (15 分)
对于给定的无向图以及图中的两个顶点，计算两个顶点所在的连通分量中的顶点数，并且判断这两个顶点之间是否有路径。

输入格式:
第一行是不超过20的正整数N，表示图有N个顶点，顶点的编号即0~N-1；

接下来N行，是N*N的邻接矩阵，矩阵的元素间用空格分隔；

最后一行是用空格隔开的两个顶点编号v和w

输出格式:
第一行输出v所在的连通分量的顶点数

第二行输出w所在的连通分量的顶点数

第三行，若v和w之间有路径，则输出Yes，否则输出No

注意：当v和w是同一个顶点时，认为v和w之间是有路径的。

输入样例: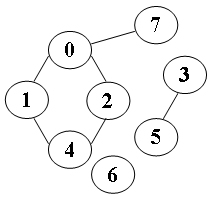

8
0 1 1 0 0 0 0 1
1 0 0 0 1 0 0 0
1 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 1 1 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0
1 3

输出样例:

5
2
No

代码
无向图的连通分量所包含点的数量，遍历即可；
是否连通，还是遍历，从v走到w即可；

#include<stdio.h>
#include<set>
#include<iostream>
#include<stack>
using namespace std;
int a[20];
int b[20][20];

int numOfNode(int v,int N)
{
    stack<int> s;
    for(int i=0;i<N;i++)a[i]=0;
    int count =1;
    a[v]=1;
    for(int i=0;i<N;i++)
        if(b[v][i]==1&&a[i]==0)s.push(i);
    int tem;
    while(!s.empty())
    {
        tem = s.top();
        s.pop();
        if(a[tem]==0)
        {
            count++;
            a[tem]=1;
            for(int i=0;i<N;i++)if(b[tem][i]==1&&a[i]==0)s.push(i);
        }
    }
    return count;
}
bool isConnect(int v,int w,int N)
{
    if(v == w)return true;
    stack<int> s;
    for(int i=0;i<N;i++)a[i]=0;
    a[v]=1;
    for(int i=0;i<N;i++)
        if(b[v][i]==1&&a[i]==0)
        {
            if(i==w)return true;
            else s.push(i);
        }
    int tem;
    while(!s.empty())
    {
        tem = s.top();
        s.pop();
        if(a[tem]==0)
        {
            a[tem]=1;
            for(int i=0;i<N;i++)if(b[tem][i]==1&&a[i]==0)
            {
                if(i==w)return true;
                else s.push(i);
            }
        }
    }
    return false;
}

int main()
{

    int N;
    cin >>N;
    for(int i=0;i<N;i++){
        a[i]=0; //未访问；
        for(int j=0;j<N;j++){
            cin >>b[i][j];
        }
    }
    int v,w;
    cin>>v>>w;
    cout<<numOfNode(v,N)<<endl;
    cout<<numOfNode(w,N)<<endl;
    if(isConnect(v,w,N))cout<<"Yes"<<endl;
    else cout<<"No"<<endl;
    return 0;
}

总体来说，这门课的习题简单，但课堂上的内容很丰富，老师讲得也很认真，很受益！