1. 栈

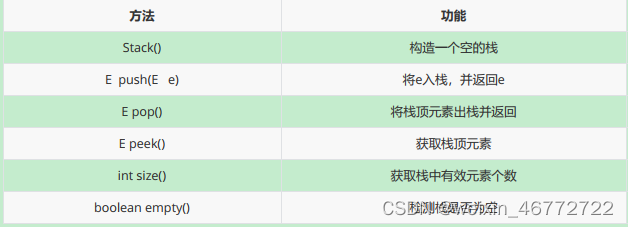
实现自己的栈

public class MyStack {
    public int[] elem;
    public int usedSized;//当前栈中存储有效数据的个数，也是当前存放数据元素的下标
    public static final int DEFAULE_SIZE = 10;
    public MyStack(){
        elem = new int[DEFAULE_SIZE];
    }

    //压栈
    public boolean empty(){
        if(usedSized == elem.length){
            return true;
        }
        return false;
    }
    public void push(int val){
        //判断是否栈满
        if(empty()){
            elem = Arrays.copyOf(elem,2*elem.length);
        }
        //存放当前的下标，同时usedSized需要自增
        elem[usedSized] = val;
        usedSized++;
    }
    //删除栈顶元素
    public boolean isEmpty(){
        return usedSized==0;
    }
    public int pop(){
        if(isEmpty()){
            throw new EmptyStackException("栈为空了！");
        }
        int oldVal = elem[usedSized-1];
        usedSized--;
        return oldVal;
    }
    //获取栈顶元素，但是不删除
    public int peek(){
        if(isEmpty()){
            throw new EmptyStackException("栈为空了！");
        }
        return elem[usedSized-1];
    }
    //大小
    public int getUsedSized(){
        return usedSized;
    }
}

 2. 队列

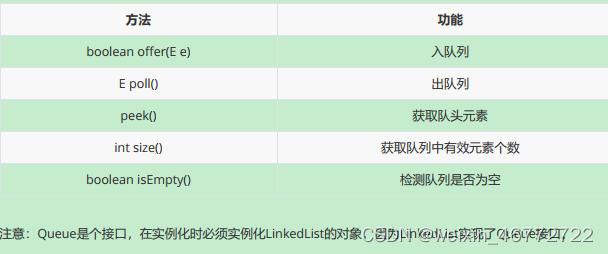
 即Queue<Integer> q = new LinkedList<>();

实现队列：

public class MyQueue {
    static class Node{
        public int val;
        public Node next;

        public Node(int val) {
            this.val = val;
        }
    }

    public Node head;//队列的头
    public Node tail;//队列的尾
//************************************************入队***********************************************
    public void offer(int val){
        Node node = new Node(val);
        if(head == null){
            head = node;
            tail = node;
        }else{
            tail.next = node;
            tail = tail.next;
        }
    }
//************************************************出队***********************************************
    public int poll(){
        if(head == null){
            return -1;
        }
        int oldVal = head.val;
        if(head.next==null){
            head = tail =null;
        }else{
            head = head.next;
        }
        return oldVal;
    }
//************************************************查看对头元素***********************************************
    public int peek(){
        if(head==null){
            return -1;
        }
        return head.val;
    }
}

 3. 由栈实现到队列

注意：需要创建两个栈：如果stack2中不为空则出栈stack2里面的，如果为空则把stack1里的全部倒到stack2中再去出栈

class MyQueue {
    Stack<Integer> stack1;
    Stack<Integer> stack2;


    public MyQueue() {
        stack1 = new Stack<>();
        stack2 = new Stack<>();
    }

    public void push(int x) {
        stack1.push(x);
    }

    public int pop() {
        if(empty()){
            return -1;
        }
        if (stack2.empty()){
            //需要把stack1的元素全部倒出来
            while (!stack1.empty()){
                stack2.push(stack1.pop());
            }
        }
        //如果stack2中不为空则出栈stack2里面的，如果为空则把stack1里的全部倒到stack2中再去出栈
        return stack2.pop();
    }

    public int peek() {
        if(empty()){
            return -1;
        }
        if (stack2.empty()){
            //需要把stack1的元素全部倒出来
            while (!stack1.empty()){
                stack2.push(stack1.pop());
            }
        }
        //如果stack2中不为空则出栈stack2里面的，如果为空则把stack1里的全部倒到stack2中再去出栈
        return stack2.peek();

    }

    public boolean empty() {
        return stack1.empty() && stack2.empty();

    }
}

 4. 由队列实现到栈

class MyStack {
    Queue<Integer> qu1;
    Queue<Integer> qu2;
    int useSizes;

    public MyStack() {
        qu1 = new LinkedList<>();
        qu2 = new LinkedList<>();

    }

    public void push(int x) {
        if(!qu1.isEmpty()){
            qu1.offer(x);
        }else if(!qu2.isEmpty()){
            qu2.offer(x);
        }else{
            qu1.offer(x);
        }
        useSizes++;

    }

    public int pop() {
        if(empty()){
            return -1;
        }
        if(!qu1.isEmpty()){
            int curSize=qu1.size();
            for (int i = 0; i < curSize-1; i++) {
                qu2.offer(qu1.poll());
            }
            useSizes--;
            return qu1.poll();
        }else{
            int curSize=qu2.size();
            for (int i = 0; i < curSize-1; i++) {
                qu1.offer(qu2.poll());
            }
            useSizes--;
            return qu2.poll();
        }

    }

    //就是peek（）显示对尾元素
    public int top() {
        if(empty()){
            return -1;
        }
        if(!qu1.isEmpty()){
            int curSize=qu1.size();
            int ret = -1;
            for (int i = 0; i < curSize; i++) {
                ret = qu1.poll();
                qu2.offer(ret);
            }
            return ret;
        }else{
            int curSize=qu2.size();
            int ret=-1;
            for (int i = 0; i < curSize; i++) {
                ret = qu2.poll();
                qu1.offer(ret);
            }
            return ret;
        }

    }

    public boolean empty() {
        return useSizes==0;

    }
}

5. 设计一个支持 push ，pop ，top 操作，并能在常数时间(即时间复杂度为O（1）)内检索到最小元素的栈。 

所以需要借助一个辅助栈，即这里的minstack

class MinStack {
    Stack<Integer> stack;
    Stack<Integer> minstack;

    public MinStack() {
        stack = new Stack<>();
        minstack = new Stack<>();
    }

    public void push(int val) {
        stack.push(val);
        if(minstack.empty()){
            //minstack为空的时候，存一下
            minstack.push(val);
        }else{
            int peekVal = minstack.peek();
            if(val <= peekVal){
                minstack.push(val);
            }
        }
    }

    public void pop() {
        if(!stack.empty()){
            int popVal = stack.pop();
            if(popVal == minstack.peek()){
                minstack.pop();
            }
        }
    }

    public int top() {
        if(!stack.empty()){
            return stack.peek();
        }else{
            return -1;
        }

    }

    public int getMin() {
        if(!minstack.empty()){
            return minstack.peek();
        }else{
            return -1;
        }

    }
}

6.栈的一些练习

public class test {
    public static void main(String[] args) {
        String s1=  "{[]}";
        System.out.println(isValid(s1));
        String[] s2= {"2","1","+","3","*"};
        System.out.println(evalRPN(s2));
        int[] pushA ={1,2,3,4,5};
        int[] popA={4,3,5,1,2};
        System.out.println(IsPopOrder(pushA,popA));
    }


    //给定一个只包括 '('，')'，'{'，'}'，'['，']'的字符串 s ，判断字符串是否有效。
    //有效字符串需满足：
    //左括号必须用相同类型的右括号闭合。
    //左括号必须以正确的顺序闭合。
    public static boolean isValid(String s) {
        Stack<Character> stack = new Stack<>();
        for(int i=0;i<s.length();i++){
            char ch=s.charAt(i);
            if(ch=='(' || ch=='[' || ch=='{'){
                stack.push(ch);
            }else{
                //右括号多
                if(stack.empty()){
                    return false;
                }
                char top = stack.peek();//获取栈顶元素但不删除
                if(ch==')'&&top=='(' || ch=='}'&&top=='{' || ch==']'&&top=='['){
                    //说明当前字符是匹配的
                    stack.pop();
                }else{
                    //不匹配
                    return false;
                }
            }
        }
        if(stack.empty()){
            return true;
        }else{
            //左括号多
            return false;
        }

    }


    //根据 逆波兰表示法，求表达式的值。
    //有效的算符包括+、-、*、/。每个运算对象可以是整数，也可以是另一个逆波兰表达式。
    //注意两个整数之间的除法只保留整数部分
    public static int evalRPN(String[] tokens) {
        Stack<Integer> stack = new Stack<>();
        for(String x:tokens){
            if(!isOperation(x)){
                stack.push(Integer.parseInt(x));
            }else{
                int num2 = stack.pop();
                int num1 = stack.pop();
                switch(x){
                    case "+":
                        stack.push(num1+num2);
                        break;
                    case "-":
                        stack.push(num1-num2);
                        break;
                    case "*":
                        stack.push(num1*num2);
                        break;
                    case "/":
                        stack.push(num1/num2);
                        break;
                }
            }
        }
        return stack.pop();
    }
    public static boolean isOperation(String x){
        //字符串相比较不能直接用“==”，而是用equals（）函数
        if(x.equals("+")||x.equals("-")||x.equals("*")||x.equals("/")){
            return true;
        }else{
            return false;
        }
    }

    //输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。
    // 假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，
    // 但4,3,5,1,2就不可能是该压栈序列的弹出序列。
    public static boolean IsPopOrder(int [] pushA,int [] popA) {
        if(pushA.length == 0 || popA.length == 0){
            return false;
        }
        Stack<Integer> stack = new Stack<>();
        int j= 0;
        for(int i=0;i<pushA.length;i++){
            stack.push(pushA[i]);
            while(j<popA.length && !stack.empty() && stack.peek().equals(popA[j])){
                //如果pushA和popA是分开的两个栈，则它们相比较不能直接用“==”，而是用equals（）函数
                stack.pop();
                j++;
            }
        }
        return stack.empty();
    }
}