
如上图,蚂蚁沿什么方向跑路才能活?
函数:z = f ( x , y ) z=f(x,y)z=f(x,y)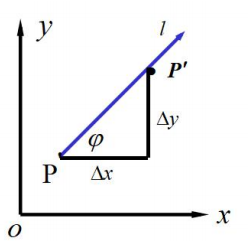
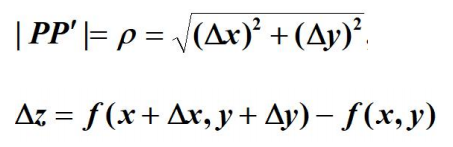
如果函数的增量,与这两点距离的比例存在,则称此为在P点沿着L的方向导数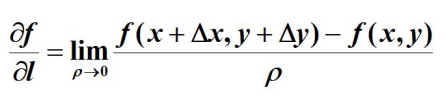
函数: f ( x , y ) f(x,y)f(x,y)在X轴正向e 1 ⃗ = { 1 , 0 } \vec{e_1}=\{1,0\}e1={1,0} ,Y轴正向$\vec{e_2}={0,1 }$ 的方向导数
分别为: f x , f y f_x,f_yfx,fy负方向导数:− f x , − f y -f_x,-f_y−fx,−fy
定理:如果函数 z = f ( x , y ) z=f(x,y)z=f(x,y)在点 P ( x , y ) P(x,y)P(x,y)是可微分的,那么在该点 沿任意方向L的方向导数都存在。
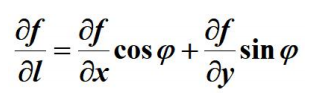
φ 为 X 轴 到 L 的 角 度 \varphi 为X轴到L的角度φ为X轴到L的角度
###例:
求 函 数 z = x e 2 y 在 点 P ( 1 , 0 ) 处 沿 从 点 P ( 1 , 0 ) 到 点 Q ( 2 , − 1 ) 的 方 向 导 数 . 求函数z=xe^{2y}在点P(1,0)处沿从点P(1,0)到点Q(2,-1)的方向导数.求函数z=xe2y在点P(1,0)处沿从点P(1,0)到点Q(2,−1)的方向导数.
解: 这里方向l ⃗ \vec{l}l即为$\vec{PQ}={1,-1}$,故x轴到方向l ⃗ \vec{l}l的转角φ = − π 4 . \varphi=-\frac{\pi}{4}.φ=−4π.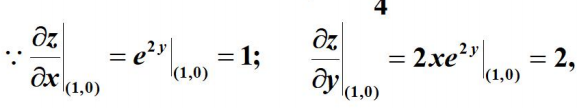
所求方向导数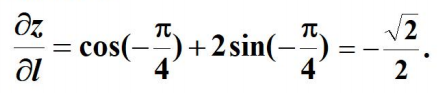
版权声明:本文为qq_28286027原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。