ElemType在数据结构中通常指element type（元素的类型），本文使用typedef自定义ElemType和Status为int类型。

typedef int ElemType;
typedef int Status;

查找：

int LocateElem(SqList L, ElemType e,
	Status(*compare)(ElemType , ElemType )) //查找顺序表中的特定元素
{		
    int i = 1;
	int *p = L.elem;    //p的初值为第一个元素的存储位置
	while (i <= L.length && !(*compare)(*p++, e)) ++i;
	if (i <= L.length) return i;    //若存在，返回元素的位置
	else return 0;    //若不存在，返回假
}
int IsEqual(ElemType a, ElemType b) //两个变量的比较，相同返回真
{
	if (a == b) return 1;
	else return 0;
}

插入：

Status ListInsert(SqList& L, int i, ElemType e) //顺序表的元素插入
{	
	int j;
	for (j = L.length - 1; j >= i - 1; --j)
		L.elem[j + 1] = L.elem[j];    //插入位置及之后的元素向右移
	L.elem[i - 1] = e;                //在指定位置插入新的元素
	++L.length;
	return 0;
}

考虑移动元素的平均情况，线性表长度为n。则：

（1）在第i个元素之前插入的概率为Pi，插入一个元素所需要移动元素次数的期望值为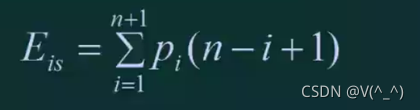

（2）在任何一个位置上插入的概率相等， 插入一个元素所需要移动元素次数的期望值为

                  Pi=1/(n+1),Eis=n/2

删除：

Status ListDelete(SqList& L,int i,ElemType &e)    //顺序表的元素删除 
{		
	if((i<1)||(i>L.length )) //所选择的删除位置不合法
		return 0;
	int *p=&(L.elem [i-1]);  //删除元素对应地址
	e=*p;                    //删除位置上的元素，可以添加输出语句，增加可读性
	int *q=L.elem+L.length-1;//顺序表尾的地址
	for(++p;p<=q;++p) *(p-1)=*p;
	--L.length;              //表长减一
	return 1;
}

考虑移动元素的平均情况，线性表长度为n。则：

（1）删除第i个元素的概率为Qi，删除一个元素所需移动元素次数的期望值为：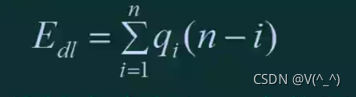

（2）删除任何一个位置上的元素概率相等，移动元素的期望值为：

       Qi=1/n,Edl=(n-1)/2 

主函数：

int main(void) {
	int i,j;
	SqList L;
	InistSqList(L);
	CreateSqList(L);
	i=LocateElem(L, 12, IsEqual);	//查找顺序表中特定元素12 
	cout << i << endl;
	ListInsert(L,2,9);				//在顺序表中第2位插入元素9 
	PrintSqList(L);
	ListDelete(L,2,j);				//在顺序表中删除第2位元素 
	PrintSqList(L);
}

关于SqList，InistSqList，CreateSqList，PrintSqList函数，代码和用法都在《线性表的基本创建和输入输出》一文中

https://blog.csdn.net/qq_56805519/article/details/120061213?spm=1001.2014.3001.5501