1.Introduction
K-Means算法是无监督的聚类算法,它实现起来比较简单,聚类效果也不错,因此应用很广泛。K-Means算法有大量的变体,本文就从最传统的K-Means算法讲起,在其基础上讲述K-Means的优化变体方法。包括初始化优化K-Means++, 距离计算优化elkan K-Means算法和大数据情况下的优化Mini Batch K-Means算法。
2.Algorithm

K-Means采用的启发式方式很简单,用下面一组图就可以形象的描述。
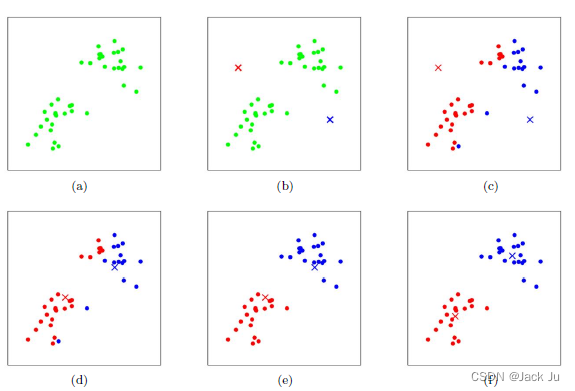
上图a表达了初始的数据集,假设k=2。在图b中,我们随机选择了两个k类所对应的类别质心,即图中的红色质心和蓝色质心,然后分别求样本中所有点到这两个质心的距离,并标记每个样本的类别为和该样本距离最小的质心的类别,如图c所示,经过计算样本和红色质心和蓝色质心的距离,我们得到了所有样本点的第一轮迭代后的类别。此时我们对我们当前标记为红色和蓝色的点分别求其新的质心,如图4所示,新的红色质心和蓝色质心的位置已经发生了变动。图e和图f重复了我们在图c和图d的过程,即将所有点的类别标记为距离最近的质心的类别并求新的质心。最终我们得到的两个类别如图f。
当然在实际K-Mean算法中,我们一般会多次运行图c和图d,才能达到最终的比较优的类别。
算法流程:
3. Coding Using C++
笔者根据上述的原理,使用C++写了一个聚类算法的demo,如下:
/**
* @Function:K-means for Cluster algorithm
* @Date:2022-09-05 14:09:00
* @Create by:juchunyu
* @Last modified:juchunyu
*/
#include<iostream>
#include<vector>
#include<math.h>
using namespace std;
#define SIZE 6
#define LENGTH 3
int main(){
int sample[SIZE][2] = {1,2,1,3,100,100,100,90,300,500,300,480};//模拟输入四个样本(1,2),(1,3),(100,100),(100,90),(300,500),(300,480)
double classIfy[1000] = {0}; //1表示类别1,2表示类别2
double mCenter[LENGTH][2] = {0,0,50,50,200,200}; //初始质心坐标
double mCenterTemp[LENGTH][2] = {0};
int iterations = 10000; //最大迭代次数
double tolerance = 0.1; //收敛条件
for(int t = 0;t < iterations;t++){
/**Start Cluster**/
for(int i = 0;i < SIZE;i++){
double minDistance = 100000000;
for(int j = 0;j < LENGTH;j++){
double distance = (sample[i][0]-mCenter[j][0]) * (sample[i][0]-mCenter[j][0]) + (sample[i][1]-mCenter[j][1]) * (sample[i][1]-mCenter[j][1]);
distance = sqrt(distance);
if(distance < minDistance){
minDistance = distance;
classIfy[sample[i][0]] = j + 1;
}
}
//重新计算mCenter
for(int j = 0;j < LENGTH; j++){
double xCenter = 0;
double yCenter = 0;
int xNum = 0;
for(int i = 0;i < SIZE;i++){
if(classIfy[sample[i][0]] == j + 1){
xCenter += sample[i][0];
yCenter += sample[i][1];
xNum ++;
}
}
mCenterTemp[j][0] = xCenter/xNum;
mCenterTemp[j][1] = yCenter/xNum;
}
}
//计算初始误差
double err = 0;
for(int i = 0;i < LENGTH;i++){
err += sqrt((mCenter[i][0]-mCenterTemp[i][0]) * (mCenter[i][0]-mCenterTemp[i][0]) + (mCenter[i][1]-mCenterTemp[i][1]) * (mCenter[i][1]-mCenterTemp[i][1]));
}
if(err < tolerance){
cout<<"Results Have Been Found!"<<endl;
break;
}
for(int j = 0;j < LENGTH;j++){
mCenter[j][0] = mCenterTemp[j][0];
mCenter[j][1] = mCenterTemp[j][1];
}
}
//输出质心结果
cout<<"mCenter"<<endl;
for(int i = 0;i < LENGTH;i++){
cout<<"(";
for(int j = 0;j < 2;j++){
cout<<mCenter[i][j]<<" ";
}
cout<<")"<<endl;
}
//输出不同的簇集合
for(int j = 0;j < LENGTH;j++){
cout<<"No."<<j+1<<"Group"<<endl;
for(int i = 0;i < SIZE;i++){
if(classIfy[sample[i][0]] == j+1){
cout<<"("<<sample[i][0]<<","<<sample[i][1]<<")";
}
cout<<endl;
}
}
}
4.Performance
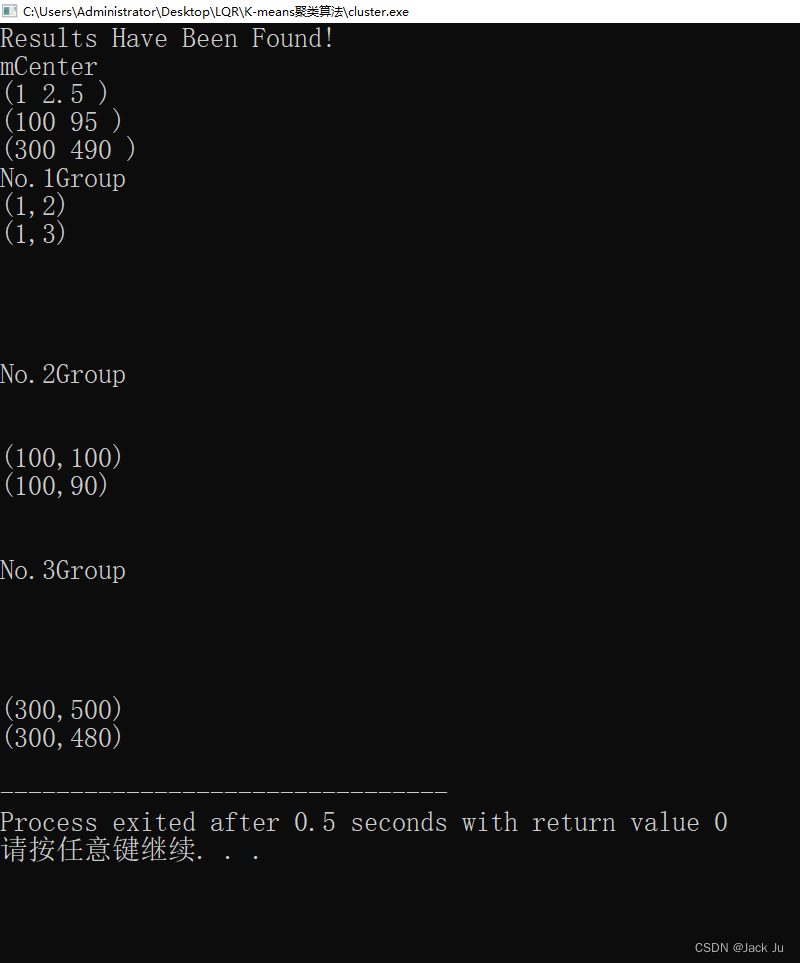
我们注意到(1,2),(1,3),(100,100),(100,90),(300,500),(300,480)被分成了三大类:
No.1Group
(1,2)
(1,3)
No.2Group
(100,100)
(100,90)
No.3Group
(300,500)
(300,480)
其质心坐标为:
(1 2.5 )
(100 95 )
(300 490 )
笔者在调试发现,初始质心的个数以及质心的坐标很重要,关系最后算法聚类的效果