IR1-中间代码生成概述

1. Intermediate Representation (IR)

- 精确:不能丢失源程序的信息
- 独立:不依赖特定的源语言与目标语言(如,没有复杂的寻址方式)
- 图(抽象语法树)、三地址代码、C语言:C语言也可以作为中间代码,比如Haskel和早期的C++
2. 表达式的有向无环图
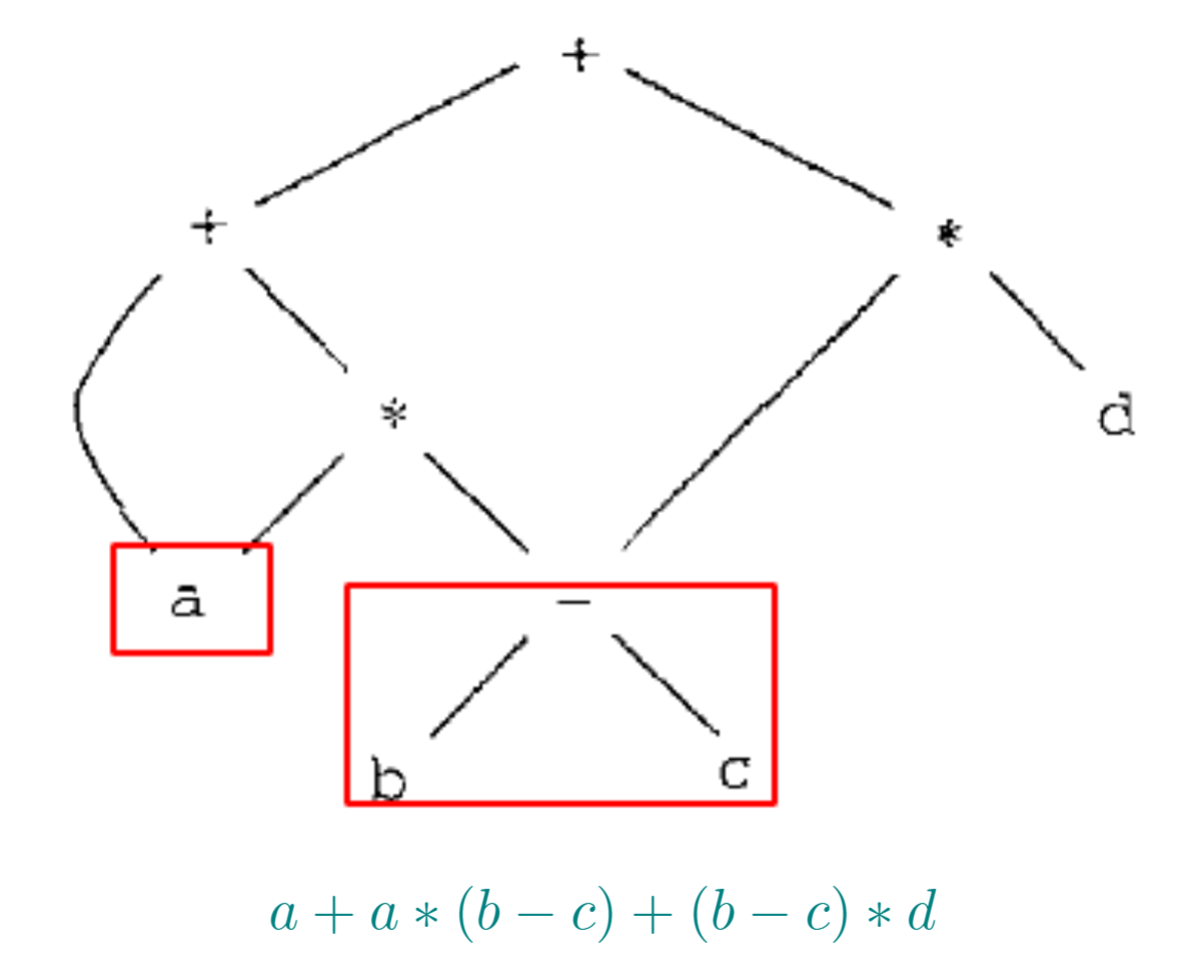
针对生成的有向无环图来生成中间表示是合适的。

在创建节点之前,先判断是否已存在(哈希表),如果已经常见直接用指针指向即可。
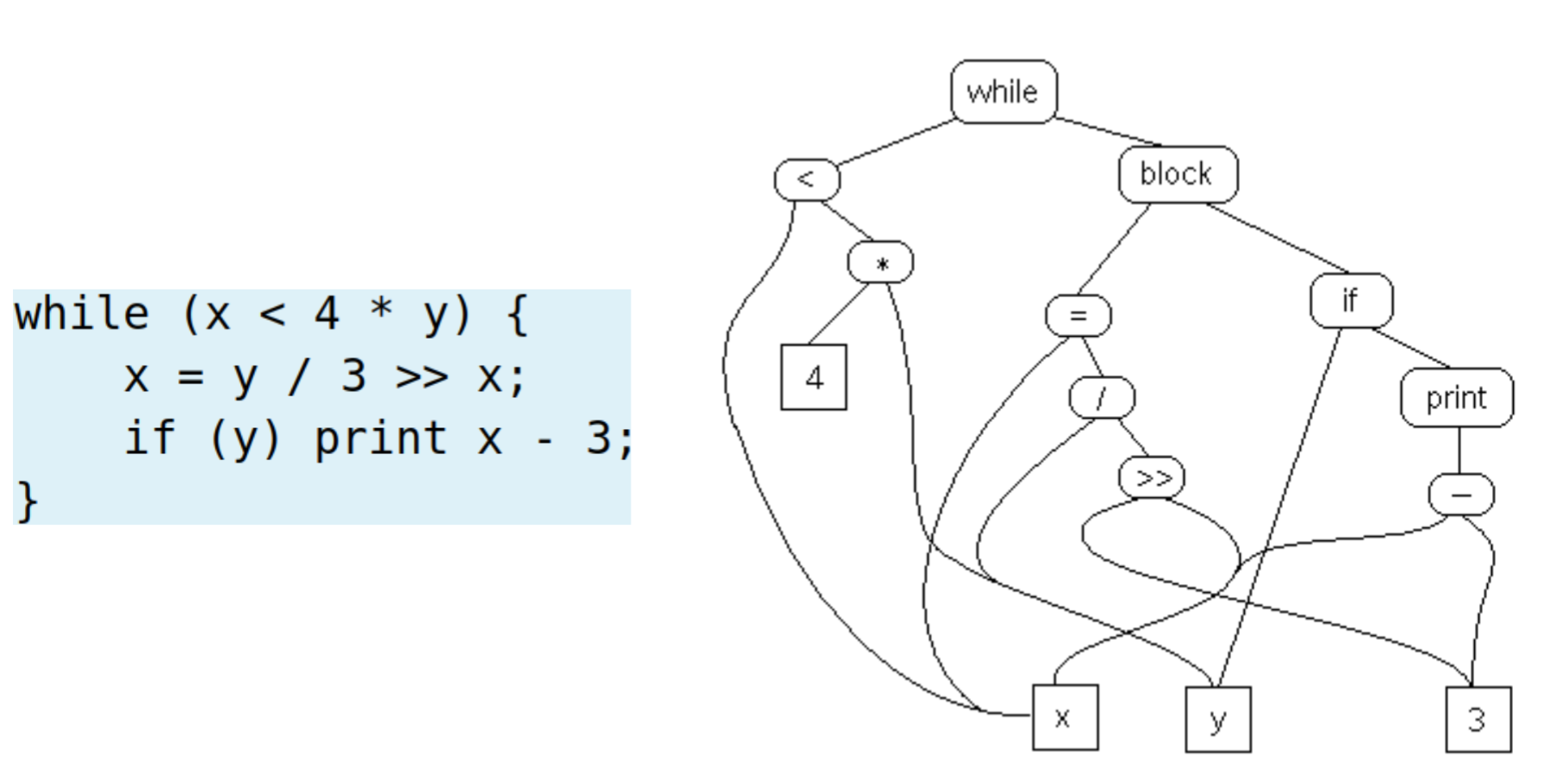
3. Definition (三地址代码(Three-Address Code (TAC; 3AC)))
每个TAC指令最多包含三个操作数。
- 三地址代码指令
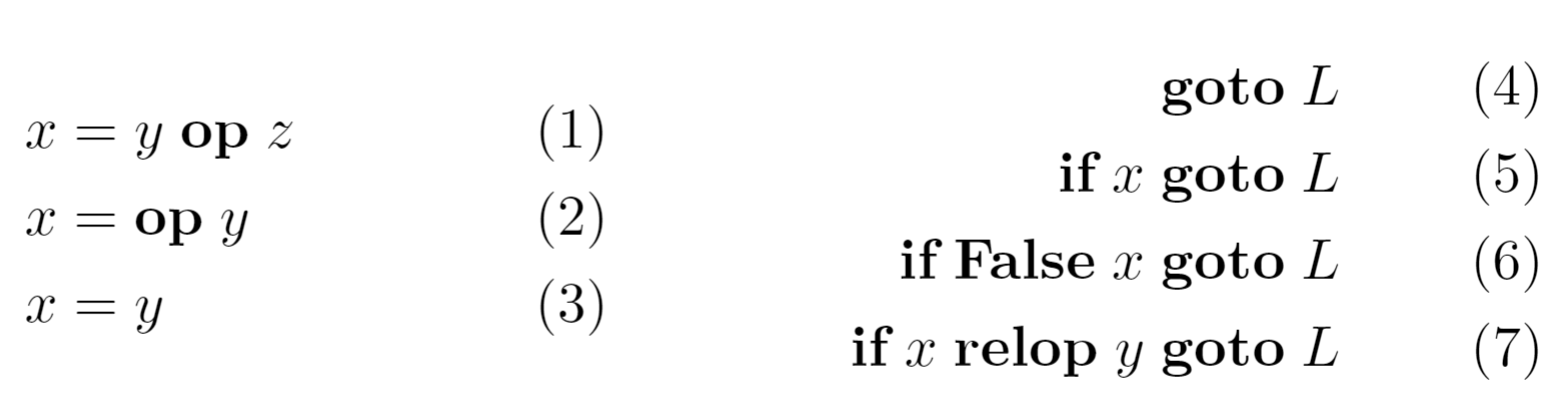
- 调用p函数,有n个参数,返回值为y

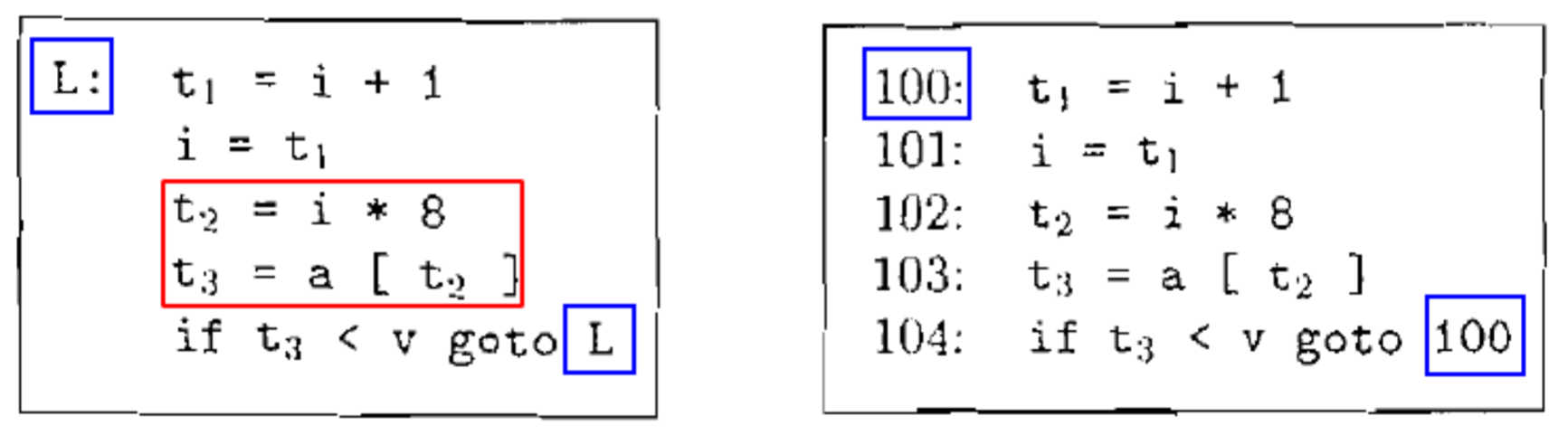
- 数组则要涉及到地址距离计算
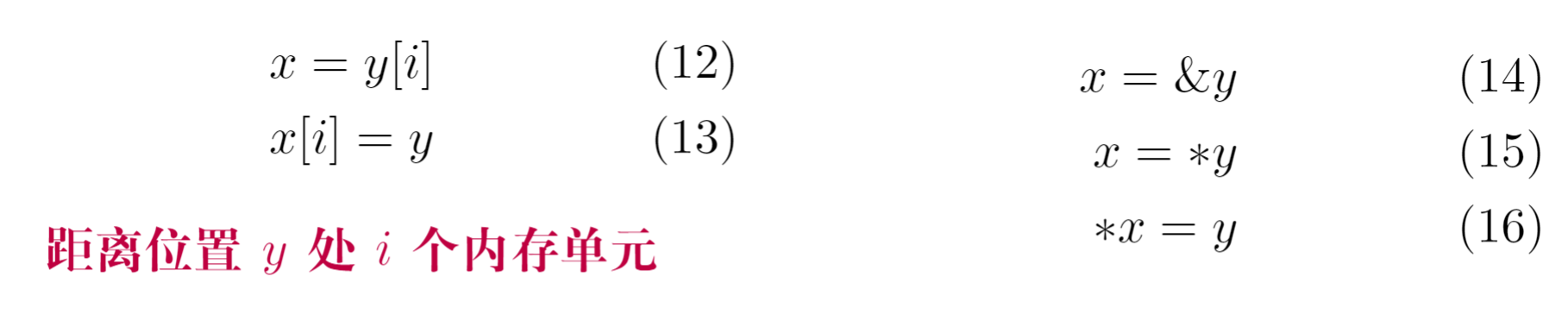
d o i = i + 1 ; w h i l e ( a [ i ] < v ) ; \begin{aligned} &do \\ &\qquad i = i + 1;\\ &while(a[i] < v); \end{aligned}doi=i+1;while(a[i]<v);
由于三地址代码,所以我们会引入大量的中间代码
4. 三地址代码的四元式表示
代码优化暂时不考虑
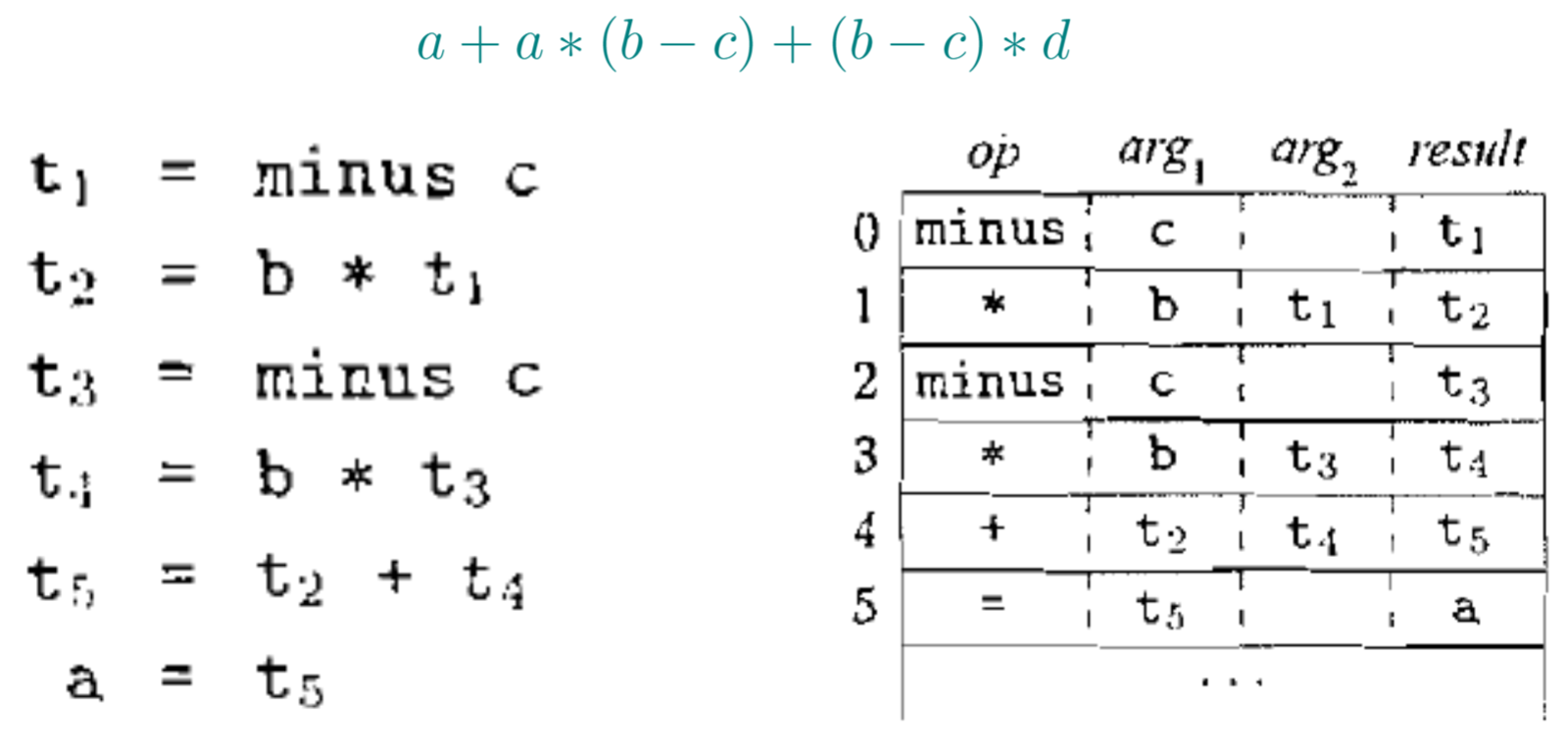
4.1. Definition (四元式(Quadruple))
一个四元式包含四个字段,分别为op、arg1、arg2与result。
- =[] 和 []= 都是我们约定好的操作符号。
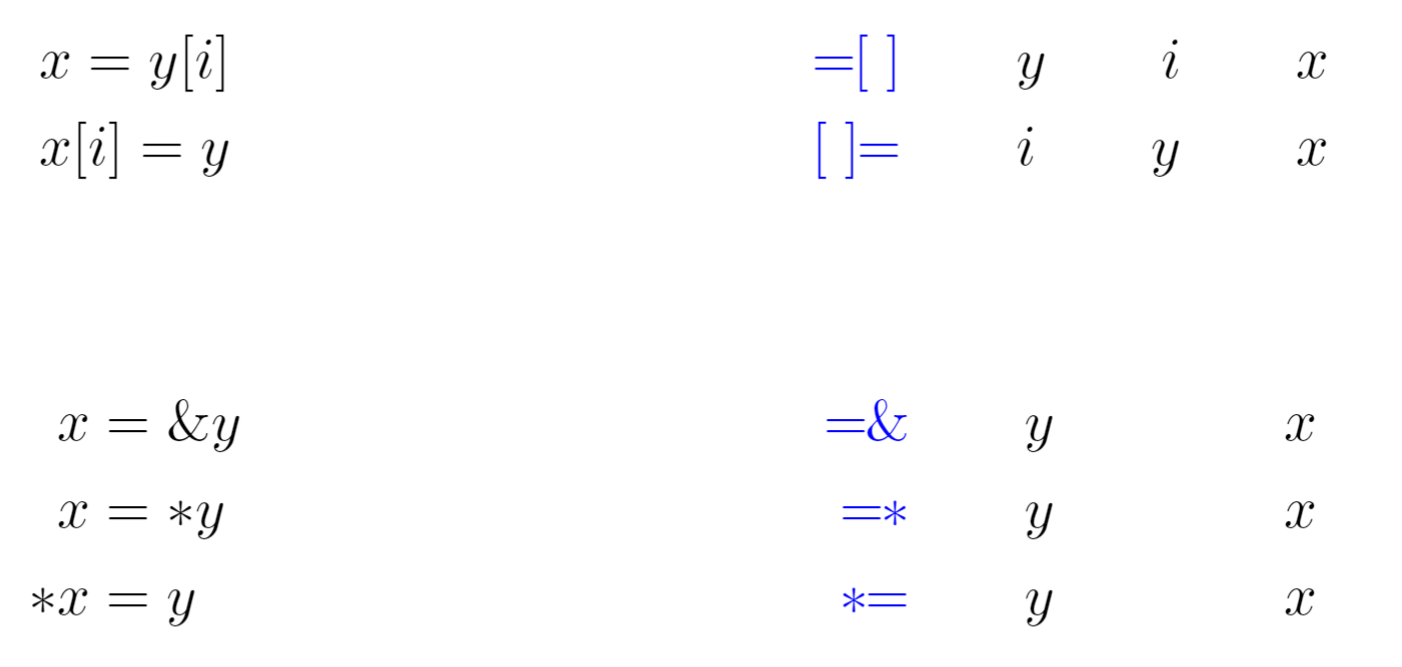
4.2. 表达式的中间代码翻译

- E . c o d e E.codeE.code是生成的中间代码
- E . a d d r E.addrE.addr是地址
- 得到E EE之前,要先知道E 1 E_1E1和E 2 E_2E2的三地址代码,然后并且赋值给E 3 E_3E3
- i d idid则是仅仅获得地址即可
- 重难点

- 只需要E . a d d r E.addrE.addr,我们使用全局缓冲区解决传递拷贝三地址代码的问题。
4.3. 表达式的中间代码翻译(增量式)

4.4. 数组引用的中间代码翻译
- 声明:i n t a [ 2 ] [ 3 ] int\ a[2][3]int a[2][3]
- 数组引用:x = a [ 1 ] [ 2 ] ; a [ 1 ] [ 2 ] = x x=a[1][2];a[1][2] =xx=a[1][2];a[1][2]=x
- 需要计算a [ 1 ] [ 2 ] a[1][2]a[1][2]的相对于数组基地址a的偏移地址
语法分析格式分析
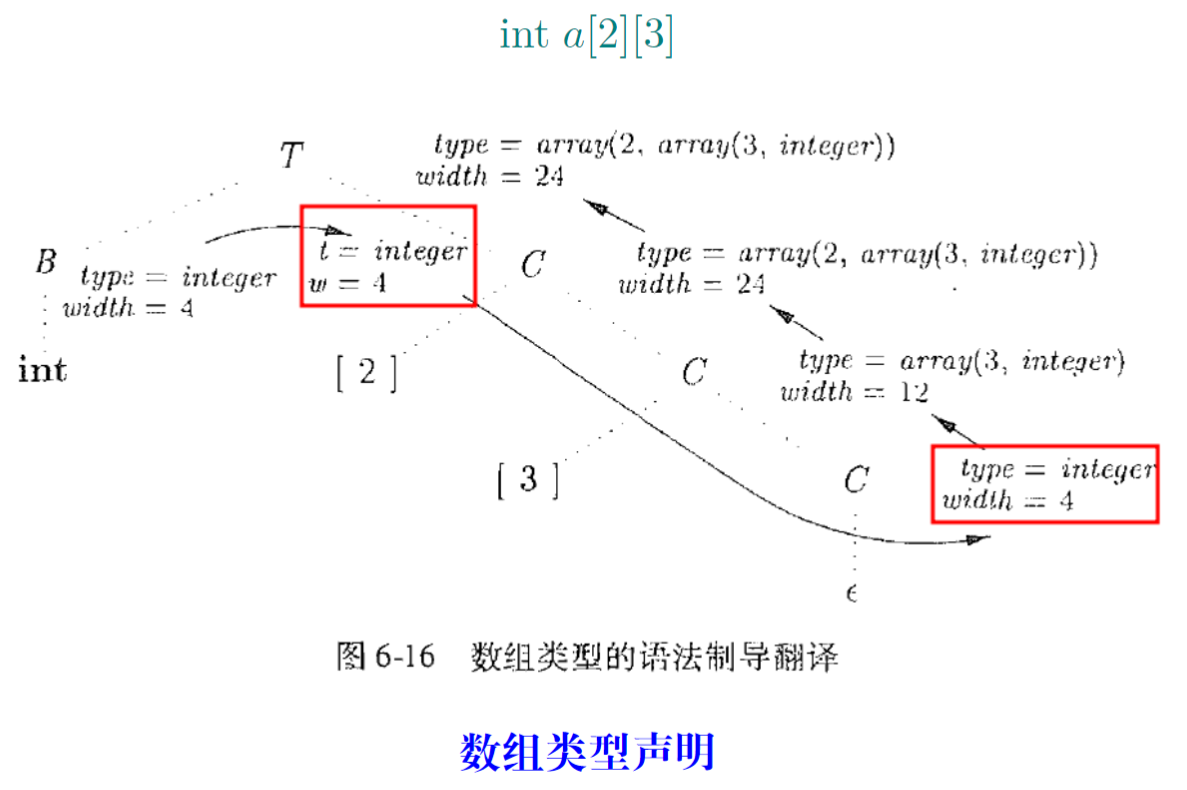
存储空间推导

复杂的SDT实现

4.4.1. 和L相关的综合属性
- 综合属性L . a r r a y . b a s e L.array.baseL.array.base:数组基地址(即,数组名),符号表可以查找到
- 综合属性L . a d d r L.addrL.addr:偏移地址

4.4.2. 和L相关的产生式
综合属性L . a r r a y L.arrayL.array:数组名id对应的符号表条目

综合属性L . t y p e L.typeL.type:(当前)元素类型

综合属性L . a d d r L.addrL.addr:(当前)偏移地址

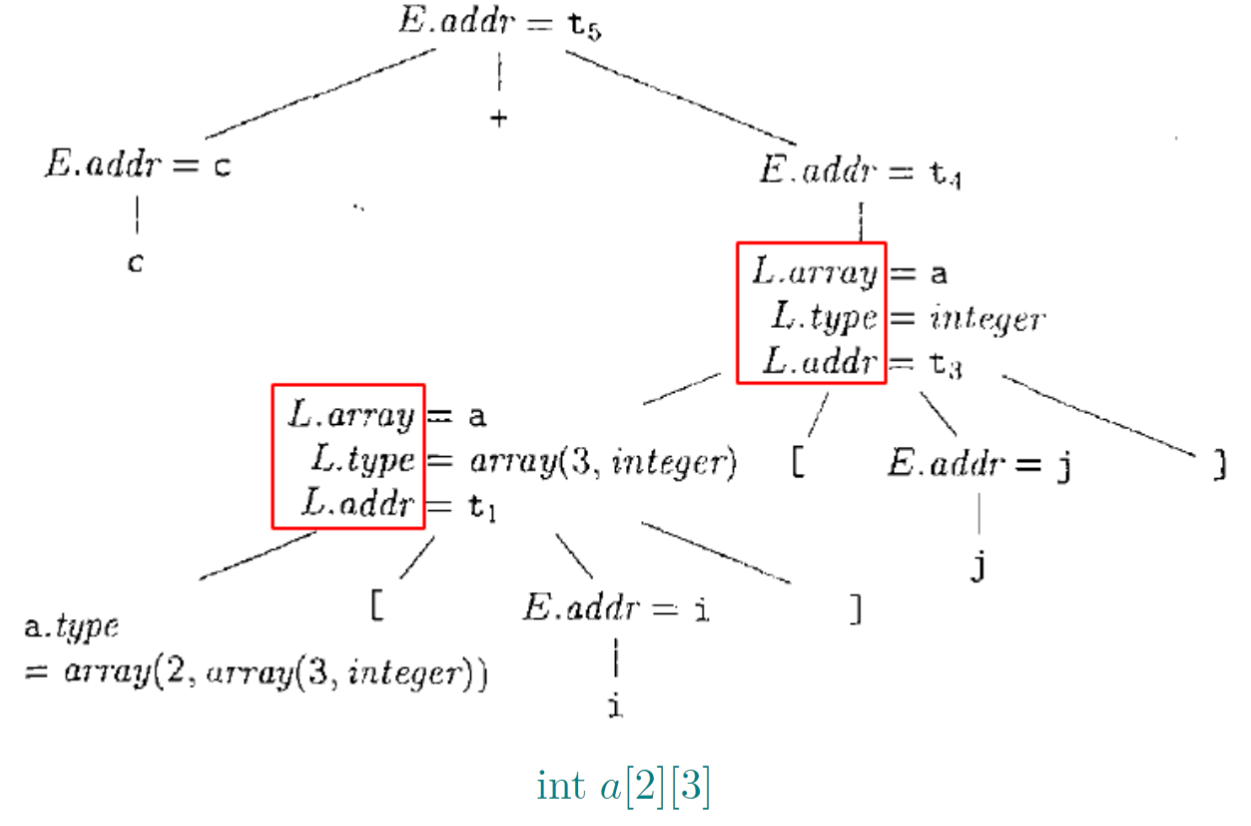
t 1 = i ∗ 12 t 2 = j ∗ 4 t 3 = t 1 + t 2 t 4 = a [ t 3 ] t 5 = c + t 4 i n t a [ 2 ] [ 3 ] \begin{array}{l} t_1 = i * 12 \\ t_2 = j * 4 \\ t_3 = t_1 + t_2 \\ t_4 = a[t_3] \\ t_5 = c + t_4 \\ \\ int\ a[2][3]\\ \end{array}t1=i∗12t2=j∗4t3=t1+t2t4=a[t3]t5=c+t4int a[2][3]
版权声明:本文为qq_44202160原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。