矩阵最小二乘法（正规方程化）

在机器学习中，若有多个特征值，可以使用此方法：

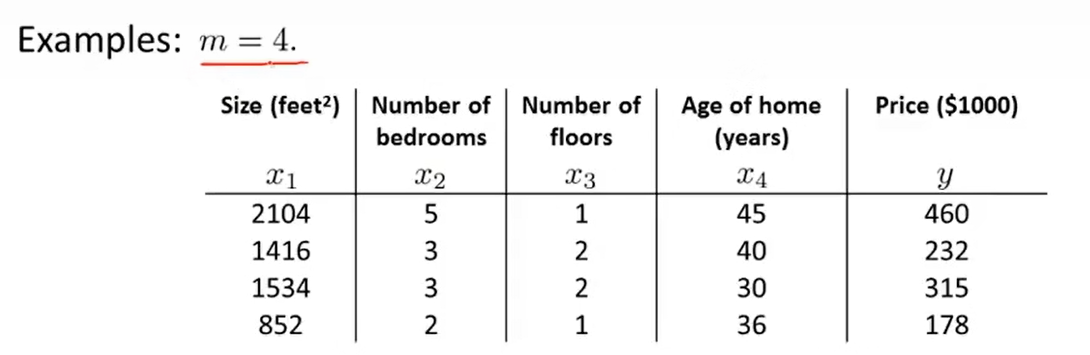
 比如这里有4个特征值，其中y那一列表示的是真实结果，以矩阵的形式表示为：

 其中

则损失函数=（预测值-真实值）^2，为什么使用平方呢？有这两个优点：

1.为了抵消正负误差相抵消

2.扩大大的误差，缩小小的误差

 至于中间两项为什么能合并，会在底部解释，然后利用矩阵求导的理论对矩阵求导：

 ，这样就得出了正规化方程，在特征值不多的时候可以使用。

需要理解的知识点：

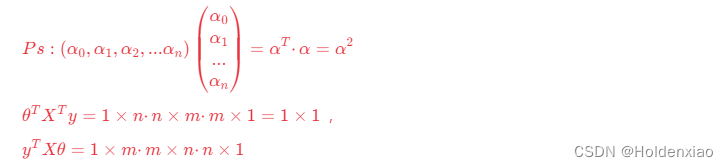
 因为中间两项其实都是标量，也就是一个1*1的数，所以可以合并一起。