判断点是否在矩形内

如图判断点P PP是否在矩形P 1 P 2 P 3 P 4 P_{1}P_{2}P_{3}P_{4}P1​P2​P3​P4​内部？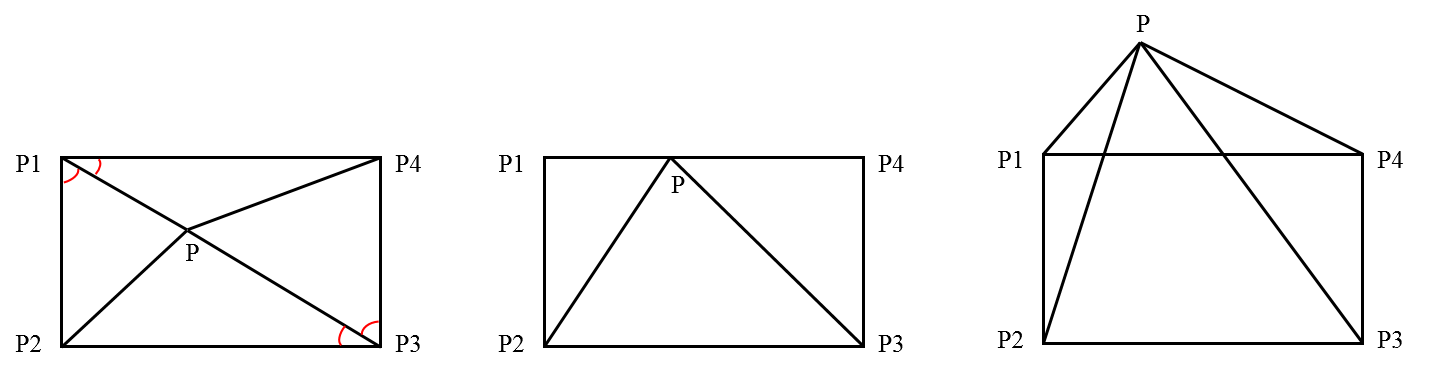
在这里插入图片描述
从上图可以看出：
点 P {P}P 位于矩形内部 ⇔ \Leftrightarrow⇔ { ∡ P P 1 P 4 ≤ 90 ∡ P P 1 P 2 ≤ 90 ∡ P P 3 P 4 ≤ 90 ∡ P P 3 P 2 ≤ 90 \left\{\begin{aligned} \measuredangle PP_{1}P_{4}\leq90\\ \measuredangle PP_{1}P_{2}\leq90\\ \measuredangle PP_{3}P_{4}\leq90 \\ \measuredangle PP_{3}P_{2}\leq90 \end{aligned}\right.⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧​∡PP1​P4​≤90∡PP1​P2​≤90∡PP3​P4​≤90∡PP3​P2​≤90​ ⇔ \Leftrightarrow⇔ { P 1 P ⃗ ⋅ P 1 P 4 ⃗ ≥ 0 P 1 P ⃗ ⋅ P 1 P 2 ⃗ ≥ 0 P 3 P ⃗ ⋅ P 3 P 4 ⃗ ≥ 0 P 3 P ⃗ ⋅ P 3 P 2 ⃗ ≥ 0 \left\{\begin{aligned} \vec{P_{1}P} \cdot \vec{P_{1}P_{4}} \geq 0\\ \vec{P_{1}P} \cdot \vec{P_{1}P_{2}} \geq 0\\ \vec{P_{3}P} \cdot \vec{P_{3}P_{4}} \geq 0\\ \vec{P_{3}P} \cdot \vec{P_{3}P_{2}} \geq 0\\ \end{aligned}\right.⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧​P1​P​⋅P1​P4​​≥0P1​P​⋅P1​P2​​≥0P3​P​⋅P3​P4​​≥0P3​P​⋅P3​P2​​≥0​
所以，点P PP在矩形P 1 P 2 P 3 P 4 P_{1}P_{2}P_{3}P_{4}P1​P2​P3​P4​内部的条件为：

P 1 P ⃗ ⋅ P 1 P 4 ⃗ ≥ 0 \vec{P_{1}P} \cdot \vec{P_{1}P_{4}} \geq 0P1​P​⋅P1​P4​​≥0&&P 1 P ⃗ ⋅ P 1 P 2 ⃗ ≥ 0 \vec{P_{1}P} \cdot \vec{P_{1}P_{2}} \geq 0P1​P​⋅P1​P2​​≥0&&P 3 P ⃗ ⋅ P 3 P 4 ⃗ ≥ 0 \vec{P_{3}P} \cdot \vec{P_{3}P_{4}} \geq 0P3​P​⋅P3​P4​​≥0&&P 3 P ⃗ ⋅ P 3 P 2 ⃗ ≥ 0 \vec{P_{3}P} \cdot \vec{P_{3}P_{2}} \geq 0P3​P​⋅P3​P2​​≥0

版权声明：本文为hhjhh76原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明。