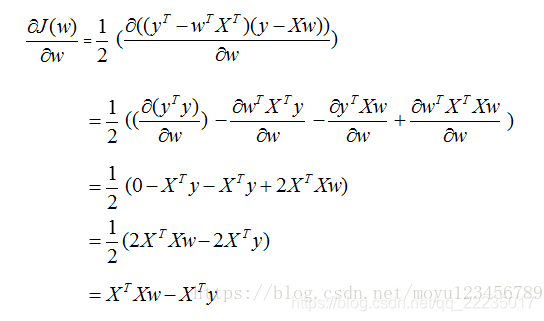本文将记录《统计学习方法》中有关逻辑回归的内容

线性回归

对于给定的数据集$D=\{x_1,y_1...x_N,y_N\}$,其中$x_i=(x_{i1},x_{i2},...,x_{id});y\in R$,线性回归的目的是找到一个线性函数可以根据输入值预测输出值。即通过对属性的线性组合得到线性函数得到其对应的输出值，计算公式为：
$$f(x)=w_1{x}_2+x_2{x}_2+...+w_d{x}_d+b$$
用向量表示为：$f(x)=wx+b$
在参数计算时，误差函数采用均方差的方法，即最小二乘法，试图找到一条直线使得所有样本到直线的距离和最短。计算公式为：
$$\begin{gathered} E(w^{\ast },b^{\ast })=min\frac{1}{2}\sum _{i=1}^N(f(x_i)-y_i{)}^2 \\ E(w^{\ast },b^{\ast })=min\frac{1}{2}\sum _{i=1}^N(y_i-w{x}_i-b{)}^2 \end{gathered}$$

1. 可以使用使用梯度下降的方法计算该参数:
   $$\begin{gathered} w=w-\alpha \ast \sum _{i=1}^N(f(x_i)-y_i)x_i) \\ b=b-\alpha \ast \sum _{i=1}^N(f(x_i)-y_i)x_i) \end{gathered}$$
2. 可以使用求极值的方法计算参数：
   $$\begin{gathered} \frac{\partial E(w,b)}{\partial w}=2(w\sum _i^N{x}_i^2-\sum _i^N(y_i-b)x_i) \\ \frac{\partial E(w,b)}{\partial b}=2(Nb-\sum _i^N(y_i-w{x}_i)) \end{gathered}$$
3. 更一般的采用矩阵计算的方式，将截距b加入参数向量中，$w=(w,b)$，是一个N+1*1的列向量，在X中将截距对应的位置设置为1,即$w_i=(x_i,1)$是一个N+1*1的横向量。则所对应的线性表达可以写成$y=x\ast w$(1*N+1乘N+1*1)
   对应的损失函数就变成了$$E(w)=min(y-xw{)}^T(y-xw)$$
   对w求导可得：$$\frac{\partial E(w)}{\partial w}=2x^T(xw-y)$$
   令上式等于0，可得
   $$w^{\ast }=(x^{T}x{)}^{-1}{x}^{T}y$$

推导如下：

求得w,带入线性回归模型中可得
$$f(x_i)=x_i(x^{T}x{)}^{-1}{x}^{T}y$$
如果$x^{T}x$不是满秩矩阵，则会求出多个W的解是最优解，常用的做法是引入正则化项，损失函数发生了变化：
$$l(w)=min\sum (f(x_i)-y_i{)}^2+\lambda L1\text{}L2$$
其中$\lambda$用来平均经验损失和正则化之间的关系，正则化为L1\L2，其中L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征的权重系数都会接近于0，在图像中可以很好的看出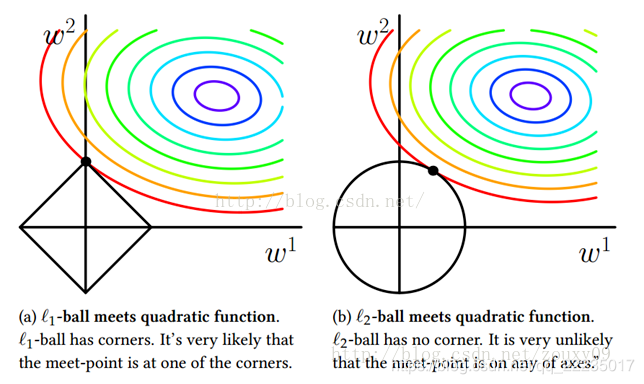
由于L1的图像为正方形，很多情况都是在坐标轴上取得，则另外一个参数就是0，这样就完成了参数稀疏化实现了降维的目的；由于L2是圆形，则每个参数不会是0，但是都很小趋向于0，这样就取消了过拟合。

在添加了正则化项L2之后的参数推导：
在L2正则化时只对特征权重W进行正则化，对偏置b不进行正则化
1.采用梯度下降的做法
$$\begin{gathered} w=w-\alpha \ast \sum _{i=1}^N(f(x_i)-y_i)x_i+\lambda w) \\ b=b-\alpha \ast \sum _{i=1}^N(f(x_i)-y_i)x_i) \end{gathered}$$
2.采用正规矩阵的做法
$$\begin{gathered} E(w)=min(y-xw{)}^T(y-xw)+\lambda w^{T}w \\ \frac{\partial E(w)}{\partial w}=x^T(xw-y)+\lambda w=0 \\ {X}^T(XW-Y)+\lambda W=0 \\ {X}^{T}XW-X^{T}Y+\lambda W=0 \\ (X^{T}X+\lambda I)W=X^{T}Y \\ W=(X^{T}X+\lambda I{)}^{-1}{X}^{T}Y \end{gathered}$$
因为$(X^{T}X+\lambda I)$肯定是可逆的，这样还顺便解决了$X^{T}X$不可逆的问题

对数线性回归

当预测值和线性函数呈指数关系时，即$ln(y)=wx+b$,实际上是将$e^{wx+b}$逼近y,但实际上是求从输入空间到输出空间的非线性映射，更一般的，都可微函数g(x)，令$y=g^{-1}(wx+b)$称为广义的线性回归。

对数几率回归

以上的线性回归模型都是回归模型，逻辑回归模型是分类模型。
当输出是二分类时，将线性回归模型产生的连续预测值转化为{0,1}类别的两值型，采用对数几率函数，将连续值转化为0到1之间的数值，得到的是具体分类的概率值，以多大的概率被分为哪个类别并且在0附近变化较陡，在其他位置变化较缓，具体公式为：
$$f(x)=\frac{1}{1+e^{-(wx+b)}}$$
可以将该公式转化为：
$$ln\frac{y}{1-y}=wx+b$$
将y认为是正例的可能性，则1-y表示了为负例的可能性，则将其认为是后验概率的话，该公式可重写为：
$$ln(\frac{p(y=1|x)}{p(y=0|x)})=wx+b$$
则拆开之后分别有：
$$\begin{gathered} p(y=1|x)=\frac{e^{wx+b}}{1+e^{wx+b}} \\ p(y=0|x)=\frac{1}{1+e^{wx+b}} \end{gathered}$$
和以上一样，令$w=(w,b);x=(x,1),则wx+b\to wx$,令$$\begin{gathered} p_1(x,w)=p(y=1|x,w) \\ {p}_0(x,w)=p(y=0|x,w) \end{gathered}$$
则每个样本的后验概率就可以被重写为：
$$p(y_i|x_i,w)=p_1^{y_i}{p}_0^{(1-y_i)}$$

$$\begin{gathered} y_i=0时p(0|x_i,w)=p_1^0{p}_0^1=p_0 \\ {y}_i=1时p(1|x_i,w)=p_1^1{p}_0^0=p_1 \end{gathered}$$

则通过最大似然法来估计w和b,
$$l(w)=\prod (p(x_i{)}^{y_i}(1-p(x_i){)}^{1-y_i})$$
将其对数化
$$l(w)=\sum _{i=1}^{N}lnp(y_i|x_i;w,b)$$

将重写之后的后验概率带入到最大似然函数中，可得
$$\begin{gathered} l(w)=\sum _{i=1}^N\{y_{i}ln(p_1)+(1-y_i)ln(p_0)\} \\ l(w)=\sum _{i=1}^N\{y_{i}ln(\frac{p_1}{p_0})+ln(p_0)\} \end{gathered}$$
则最大似然函数等价于最大化:
$$l(w)=\sum _i^N(y_{i}wx-ln(1+i{e}^{wx}))$$
利用如梯度下降和牛顿法等求得最佳解，得到最优的w:
$$\hat{w}=argminl(w)$$

逻辑回归算法总结

1. 有关sklearn的内容已经有大佬整理好了，这里搬运一下sklearn调参1 sklearn调参2
2. 在处理数据不平衡时，可以采用的方法有过采样、欠采样和再放缩
   因为逻辑回归中正例与负例的比例是$y/1-y$,只需令：
   $$\frac{y^{\prime }}{1-y^{\prime }}=\frac{y}{1-y}\ast \frac{m^{+}}{m^{-}}$$
   即实现了阈值移动，即再放缩
3. 逻辑回归中的多分类问题，不失一般的，考虑共有N个类别，拆分为两两二分类问题，拆分策略有：OVO（即一对一，两两类别之间均建立一个分类器，共有N(N-1)/2个）;OvR（即一与其他，对每一个类别与其余所有类别建立分类器，共有N个）；MvM（将样本集做M次划分，将其中一个作为正例，另一个作为负例，这样可以构建M个分类器实现编码，解码时对M个分类器构建一个编码，与每个分类器的编码进行比较，找出距离最近的一个分类器作为输出类别）