node2vec简单总结

node2vec

参考博客：https://zhuanlan.zhihu.com/p/56542707

伪代码

def node2vec_walk(G, u, walk_length):
	walk = [u]
	for l in range(walk_length):
		V = get_neighbors(G, walk[-1])
		s = alias_sample(V, pi)  # 核心的采样策略
		walk.append(s)
	
	return walk 

def node2vec(...):
	walks = []
	for r in range(walk_iter):
		for u in AllNodes:
			walk = node2vec_walk(G, u, walk_length)
			walks.append(walk)
			
	Word2Vec(walks)
	SGD()

Alias Sampling

1、首先需要根据node2vec的转移策略得到预处理的转移概率。这样，对于每个当前节点u，我们都可以知道所有邻居节点的转移概率列表，并对这个列表进行归一化得到概率。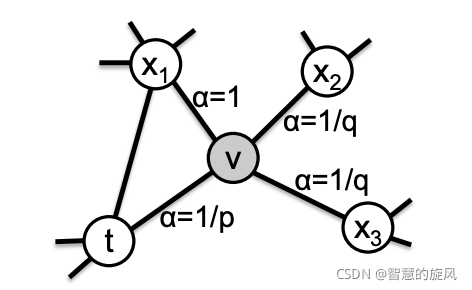

2、有了这个概率分布列表，我们就可以根据其进行alias sample，得到本次需要选出的邻居节点。
3、我们通过处理可以得到alias_table，时间复杂度是$O(n)$。这样之后每次采样的时间复杂度就是$O(1)$。

假设有N个邻居节点，转移到节点i的概率为$p_i$，则可以将全部概率看作是1*N矩形的面积，这样，$q_i$ 就可以写成 $\frac{p_i\ast N}{{\sum }_{k=1}^N{p}_k}$，如果进行归一化，那么分母就是1。有一些项乘N之后会>1，有一些会<1，那么再用>1的部分依次去补全<1的部分（最终刚好可以全部都补全）。最终随机random一个 $r\in [0,1)$和 $K\in [0,N)$，如果$r<q[K]$，那么接受事件i，否则返回alias[i]。(参考：https://zhuanlan.zhihu.com/p/54867139)