基本概念

• SVD
  奇异值分解。将矩阵进行压缩。大幅度减少内存消耗，提高运行速度。

应用

数据降维、推荐算法、自然语言处理

算法核心

$$A=U\sum V^t$$

对于任意矩阵A，我们总能够将其分解位三个矩阵$U、\sum 、V^t$

• U为酉矩阵
• $\sum$为对角阵
• $V^t$为酉矩阵

酉矩阵

• 满足$A^T=A^{-1}$

分解过程

将原始矩阵分解为三个矩阵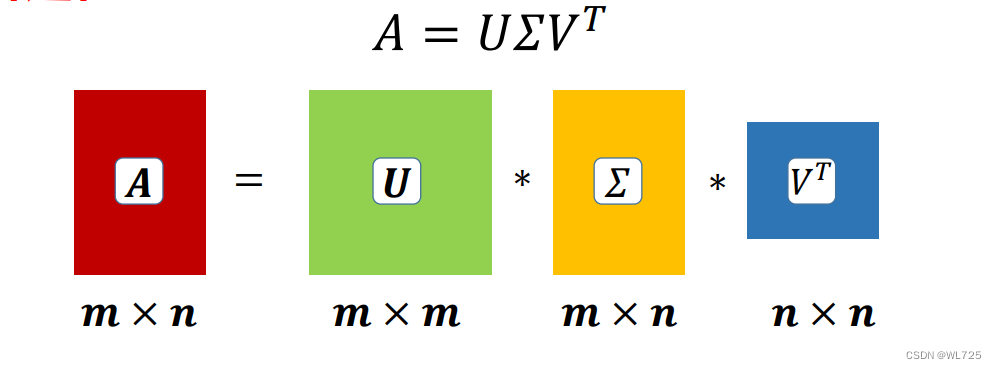

推导过程

• $A=U\sum V^t$
• $A^t=(U\sum V^t{)}^T=V(U\sum {)}^T=V{\sum }^t{U}^T$

结论

1. $A{A}^T=U\sum V^{t}V{\sum }^T{U}^T=U{\sum }^2{U}^T$
2. $A^{T}A=V{\sum }^T{U}^{T}U\sum V^t=V{\sum }^2{V}^T$

实例数据

代码演示

import numpy as np
from PIL import Image
import matplotlib.pyplot as plt


def pic_compress(k, pic_array):
    global u, sigma, vt, sig, new_pic

    u, sigma, vt = np.linalg.svd(pic_array)
    sig = np.eye(k) * sigma[: k]
    new_pic = np.dot(np.dot(u[:, :k], sig), vt[:k, :])  # 还原图像
    size = u.shape[0] * k + sig.shape[0] * sig.shape[1] + k * vt.shape[1]  # 压缩后大小
    return new_pic, size


filename = "timg.jpg"
ori_img = np.array(Image.open(filename))
new_img, size = pic_compress(100, ori_img)
print("original size:" + str(ori_img.shape[0] * ori_img.shape[1]))
print("compress size:" + str(size))
fig, ax = plt.subplots(1, 2)
ax[0].imshow(ori_img, cmap='gray')
ax[0].set_title("before compress")
ax[1].imshow(new_img, cmap='gray')
ax[1].set_title("after compress")
plt.show()

效果展示

original size:1365760