Homework-3 – 源码巴士

(a) $max\, \, Z=x_{1}+2x_{2}$

$s.t.$ $x_{1}+3x_{2}+s_{1}$ $=8$ (1)

$x_{1}+x_{2}$ $+s_{2}=4$ (2)

$x_{j}\geq 0(j=1,2),s_{i}\geq 0(i=1,2)$

For the sake of simplicity, it is rewritten as the following canonial form :

$max\, \:Z$

$s.t.$ $Z-x_{1}-2x_{2}$ $=0$ (0)

$x_{1}+3x_{2}+s_{1}$ $=8$ (1)

$x_{1}+x_{2}$ $+s_{2}=4$ (2)

(b) $\bullet$ $(x_{1},x_{2})=(0,\frac{8}{3})$ is a CPF solution of the original model;

$(x_{1},x_{2},s_{1},s_{2})=(0,\frac{8}{3},0,\frac{4}{3})$ is the corresponding augmented solution（a basic feasible solution).

$x_{1},s_{1}$ are the nonbasic variables; $x_{2},s_{2}$ are the basic variables.

$\bullet$ $(x_{1},x_{2})=(2,2)$ is a CPF solution of the original model;

$(x_{1},x_{2},s_{1},s_{2})=(2,2,0,0)$ is the corresponding augmented solution（a basic feasible solution).

$s_{1},s_{2}$ are the nonbasic variables; $x_{1},x_{2}$ are the basic variables.

$\bullet$ $(x_{1},x_{2})=(4,0)$ is a CPF solution of the original model;

$(x_{1},x_{2},s_{1},s_{2})=(4,0,4,0)$ is the corresponding augmented solution（a basic feasible solution).

$x_{2},s_{2}$ are the nonbasic variables; $x_{1},s_{1}$ are the basic variables.

$\bullet$ $(x_{1},x_{2})=(0,0)$ is a CPF solution of the original model;

$(x_{1},x_{2},s_{1},s_{2})=(0,0,8,4)$ is the corresponding augmented solution（a basic feasible solution).

$x_{1},x_{2}$ are the nonbasic variables; $s_{1},s_{2}$ are the basic variables.

When the nonbasic variables $(x_{1},s_{1})$ are set equal to zero,this BF solution also is the simultaneous solution of the system of equations obtained in part (a).

$\bullet$ $x_{1}+3x_{2}=8$ , $x_{1}+x_{2}=4$

When the nonbasic variables $(s_{1},s_{2})$ are set equal to zero,this BF solution also is the simultaneous solution of the system of equations obtained in part (a).

$\bullet$ $x_{1}+s_{1}=8$ , $x_{1}=4$

When the nonbasic variables $(x_{2},s_{2})$ are set equal to zero,this BF solution also is the simultaneous solution of the system of equations obtained in part (a).

$\bullet$ $s_{1}=8$ , $s_{2}=4$

When the nonbasic variables $(x_{1},x_{2})$ are set equal to zero,this BF solution also is the simultaneous solution of the system of equations obtained in part (a).

(d) $\bullet (x_{1},x_{2})=(0,4)$ is the corner-point infeasible solution;

$(x_{1},x_{2},s_{1},s_{2})=(0,4,-4,0)$ is the corresponding basic infeasible solution.

$x_{1},s_{2}$ are the nonbasic variables; $x_{2},s_{1}$ are the basic variables.

$\bullet (x_{1},x_{2})=(8,0)$ is the corner-point infeasible solution;

$(x_{1},x_{2},s_{1},s_{2})=(8,0,0,4)$ is the corresponding basic infeasible solution.

$x_{2},s_{1}$ are the nonbasic variables; $x_{1},s_{2}$ are the basic variables. $x_{1}$

(e) $\bullet 3x_{2}+s_{1}=8$ , $x_{2}=4$

When the nonbasic variables $(x_{2},s_{1})$ are set equal to zero,this BF solution also is the simultaneous solution of the system of equations obtained in part (a).

$\bullet x_{1}=8$ , $s_{2}=4$

When the nonbasic variables $(x_{1},s_{2})$ are set equal to zero,this BF solution also is the simultaneous solution of the system of equations obtained in part (a).

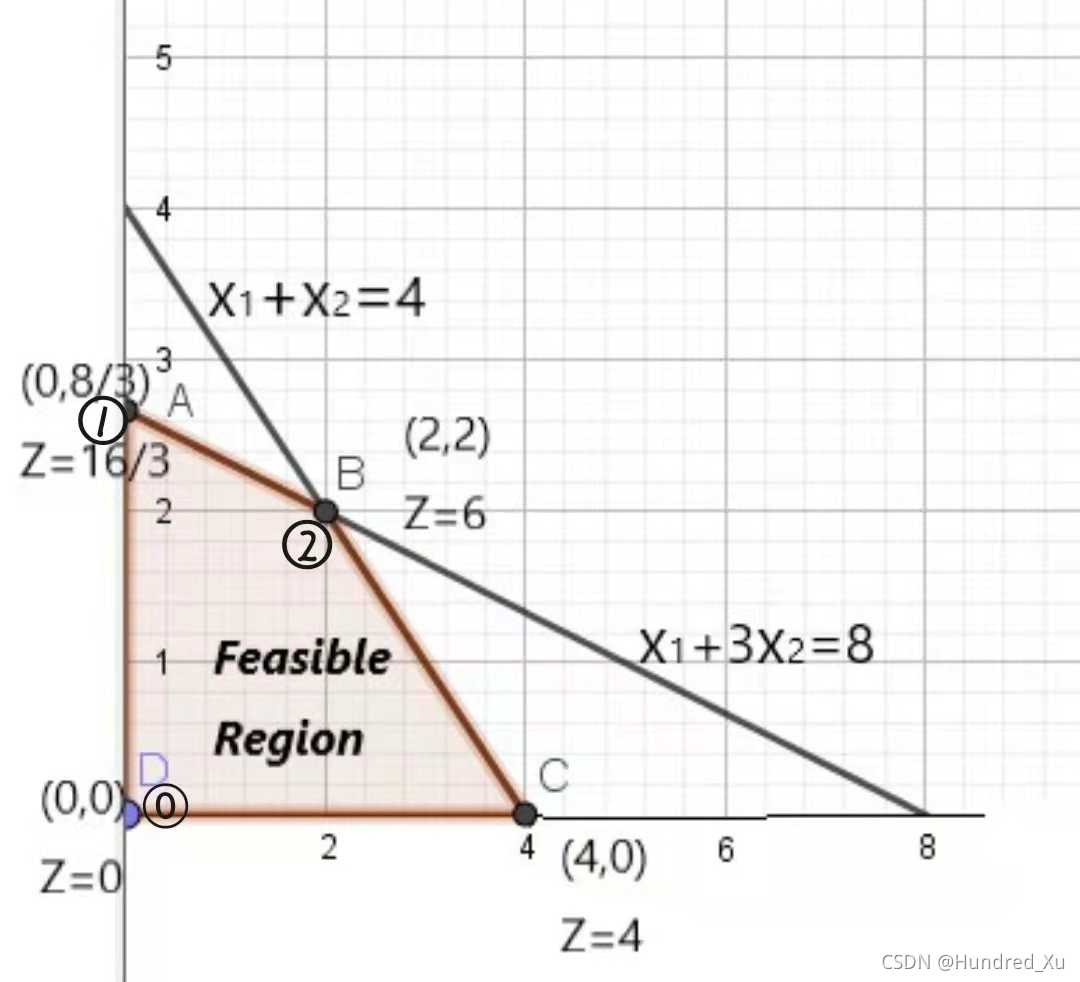
Initialization (Iteration 0)

Set $x_{1}$ and $x_{2}$ be the non-basic variables and the other variables are set to be the basic variables. Then we obtain the values of the basic variables $(s_{1},s_{2})=(8,4)$ and hence we have the initial BF solution $(x_{1},x_{2},s_{1},s_{2})=(0,0,8,4)$ .

Optimality Test

At the initial BF solution, $Z=x_{1}+2x_{2}=0$ .

Obviously,increasing the values of $x_{1}$ or $x_{2}$ can bring an improvement to Z. So, the current BF solution is NOT optimal.

Iteration 1

1.Determining Where to Go

$\bullet$ Choose the non-basic variable with largest improvement in Z.

$\bullet$ Increasing this non-basic variable from zero will convert it to a basic variable for the next BF solution. It is called the entering (basic) variable for iteration 1.

$\bullet$ Prototype Example :

Objective function : $Z=x_{1}+2x_{2}$

Rate of improvement in Z by increasing $x_{1}=1$

Rate of improvement in Z by increasing $x_{2}=2$

Thus, we should choose $x_{2}$ .

2.Determining Where to Stop

$\bullet$ Increasing $x_{2}$ increases Z , so we want to go as far as possible without leaving the feasible region.

$\bullet$ Minimum Ratio Test :

To identify the maximum possible improvement we can make with which we still inside the feasible region.

Non-basic variable : $x_{1}$ =0

(1): $s_{1}=8-3x_{2}\geq 0\Rightarrow x_{2}\leq \frac{8}{3}$

(2): $s_{2}=4-x_{2}\geq 0\Rightarrow x_{2}\leq 4$

These implies, $x_{2}\leq \frac{8}{3}$ . Therefore, we set $x_{2}=\frac{8}{3}$ .

When $x_{2}=\frac{8}{3}$ , eq.(1) gives $s_{1}=0$ and leaves the basis. ( $s_{2}$ is called the leaving (basic) variable for iteration 1.)

3.Solving for the New BF Solution

$\bullet$ The purpose of step 3 is to convert the system of equations to the canonical form. The solution can then be read easily.

$\bullet$ By elementary row operations, we solve the system of equations for $Z,x_{2},s_{2}$ :

New eq.(1)=eq.(1)/3

$\frac{1}{3}x_{1}+x_{2}+\frac{1}{3}s_{1}=\frac{8}{3}$

New eq.(0)=eq.(0)+2 $\times$ eq.(1)

$Z-\frac{1}{3}x_{1}+\frac{2}{3}s_{1}=\frac{16}{3}$

New eq.(2)=eq.(2) - New eq.(1)

$\frac{2}{3}x_{1}-\frac{1}{3}s_{2}+s_{2}=\frac{4}{3}$

The resulting canonical form of the model is：

$Z-\frac{1}{3}x_{1}$ $+\frac{2}{3}s_{1}$ $=\frac{16}{3}$ (0)

$\frac{1}{3}x_{1}+x_{2}+\frac{1}{3}s_{1}$ $=\frac{8}{3}$ (1)

$\frac{2}{3}x_{1}$ $-\frac{1}{3}s_{1}+s_{2}=\frac{4}{3}$ (2)

$\bullet$ Since $x_{1}$ and $s_{2}$ are non-basic variables, thus $x_{1}=0$ and $s_{2}=0$ and hence the new BF solution, $(x_{1},x_{2},s_{1},s_{2})=(0,\frac{8}{3},0,\frac{4}{3})$ , which yields $Z=\frac{16}{3}$ .

Optimality Test

The current eq.(0) gives the current objective function:

$Z=\frac{16}{3}+\frac{1}{3}x_{1}-\frac{2}{3}s_{1}$

Such $x_{1}$ has a positive coeffiicient, increasing $x_{1}$ would lead to an adjacent BF solution that is better than the current BF soution, so the current solution is NOT optimal.

Iteration 2

1.Determining Where to Go

Now $Z=\frac{16}{3}+\frac{1}{3}x_{1}-\frac{2}{3}s_{1}$ , Z can be increased by increasing $x_{1}$ , but not $s_{1}$ . Therefore, we choose $x_{1}$ as the entering variable.

2.Determining Where to Stop (Minimun Ratio Test)

Non-basic Variable: $s_{1}$

(1): $s_{1}=8-x_{1}-3x_{2}=0\Rightarrow x_{2}=\frac{8}{3}-\frac{1}{3}x_{1}$

(2): $s_{2}=4-x_{1}-x_{2}\geq 0\Rightarrow x_{1}\leq 4-x_{2}\Rightarrow x_{1}\leq 2$

By the minimum ratio test, we conclude that we should choose $s_{2}$ as the leaving variable and should set $x_{1}=2$ .

3.Solving for the New BF Solution

New eq.(2)=eq.(1)/2-eq.(2)/2

$x_{2}+\frac{1}{2}s_{1}-\frac{1}{2}s_{2}=2$

New eq.(1)=New eq.(2)-eq.(1)

$x_{1}-\frac{1}{2}s_{1}+\frac{3}{2}s_{2}=2$

New eq.(0)=eq.(0)+New eq.(1)+2 $\times$ New eq.(2)

$Z+\frac{1}{2}s_{1}+\frac{1}{2}s_{2}=6$

The resulting canonical form of the model is:

$Z$ $+\frac{1}{2}s_{1}+\frac{1}{2}s_{2}=6$ (0)

$x_{1}$ $-\frac{1}{2}s_{1}+\frac{3}{2}s_{2}=2$ (1)

$x_{2}+\frac{1}{2}s_{1}-\frac{1}{2}s_{2}=2$ (2)

The new BF solution is $(x_{1},x_{2},s_{1},s_{2})=(2,2,0,0)$ and the corresponding $Z=6$ .

Optimality Test

Since increasing the non-basic variables ( $s_{1}$ and $s_{2}$ ) would not increase Z, the current BF solution is optimal. The optimal BF solution is $(x_{1}^{\ast },x_{2}^{\ast },s_{1}^{\ast },s_{2}^{\ast })=(2,2,0,0)$ , which implies the optimal solution to the original problem is $(x_{1}^{\ast },x_{2}^{\ast })=(2,2)$ and the corresponding optimal value $Z^{\ast }=6$ .

Initialization (Iteration 0)

$x_{1}$ $x_{2}$ $s_{1}$ $s_{2}$

rhs

-1 -2 0 0

$s_{1}$

$s_{2}$

1 3 1 0

1 1 0 1

Optimality Test

$\bullet$ The current BF solution is optimal if and only if every coefficient in row 0 is non-negative.

$\bullet$ Now, the coefficient of both $x_{1}$ and $x_{2}$ in row 0 are negative, therefore the current BF solution is NOT optimal.

Iteration 1

1.Determining the Entering Variable (Determining Where to Go)

Select the non-basic variable with the "most negative" coefficient. The column below this coefficient is called the pivot column.

$x_{1}$ $x_{2}$ $s_{1}$ $s_{2}$

rhs

-1 -2 0 0

$s_{1}$

$s_{2}$

1 3 1 0

1 1 0 1

2.Determining the Leaving Variable by the Minimum Ratio Test (Determining Where to Stop)

Pick up the strictly positive coefficient in the pivot column and then calculate "rhs / value of pivot column's element".

Choose the variable with the minimum value of the ratio as the leaving variable. The row is called the pivot row.

$x_{1}$ $x_{2}$ $s_{1}$ $s_{2}$

rhs

ratio

-1 -2 0 0

$s_{1}$

$s_{2}$

1 3 1 0

1 1 0 1

8/3=8/3

4/1=4

3.Solving for the New BF Solution

$\bullet$ Create a coefficient 1 for the entering variable in the pivot row by multiplying the row by a suitable number.

$\bullet$ Create a coefficient 0 for the entering variable in all rows except the pivot row by adding a suitable multiple of the pivot row.

$x_{1}$ $x_{2}$ $s_{1}$ $s_{2}$

rhs

-1/3 0 2/3 0

16/3

$x_{2}$

$s_{2}$

1/3 1 1/3 0

2/3 0 -1/3 1

8/3

4/3

Optimality Test

The coefficient of $x_{1}$ in row 0 is negative, therefore the current BF solution is NOT optimal.

Iteration 2

$x_{1}$ $x_{2}$ $s_{1}$ $s_{2}$

rhs

ratio

-1/3 0 2/3 0

$x_{2}$

$s_{2}$

1/3 1 1/3 0

2/3 0 1/3 1

8/3

4/3

(8/3)/(1/3)=8

(4/3)/(2/3)=2

$x_{1}$ $x_{2}$ $s_{1}$ $s_{2}$

rhs

0 1/2 0 1/2

$x_{1}$

$x_{2}$

1 0 -1/2 3/2

0 1 1/2 -1/2

Optimality Test

Since none of the coefficient in row 0 are negative, the current BF solution is optimal.

The optimal BF solution is $(x_{1}^{\ast },x_{2}^{\ast },s_{1}^{\ast },s_{2}^{\ast })=(2,2,0,0)$ , which implies the optimal solution to the original is $(x_{1}^{\ast },x_{2}^{\ast })=(2,2)$ and the corresponding $Z^{\ast }=6$ .

Initialization (Iteration 0)

$x_{1}$ $x_{2}$ $x_{3}$ $s_{1}$ $s_{2}$ $s_{3}$

rhs

-2 1 -1 0 0 0

$s_{1}$

$s_{2}$

$s_{3}$

3 1 1 1 0 0

1 -1 2 0 1 0

1 1 -1 0 0 1

Optimality Test

$\bullet$ The current BF solution is optimal if and only if every coefficient in row 0 is non-negative.

$\bullet$ Now, the coefficient of both $x_{1}$ and $x_{3}$ in row 0 are negative, therefore the current BF solution is NOT optimal.

Iteration 1

1.Determining the Entering Variable (Determining Where to Go)

Select the non-basic variable with the "most negative" coefficient. The column below this coefficient is called the pivot column.

$x_{1}$ $x_{2}$ $x_{3}$ $s_{1}$ $s_{2}$ $s_{3}$

rhs

-2 1 -1 0 0 0

$s_{1}$

$s_{2}$

$s_{3}$

3 1 1 1 0 0

1 -1 2 0 1 0

1 1 -1 0 0 1

2.Determining the Leaving Variable by the Minimum Ratio Test (Determining Where to Stop)

Pick up the strictly positive coefficient in the pivot column and then calculate "rhs / value of pivot column's element".

Choose the variable with the minimum value of the ratio as the leaving variable. The row is called the pivot row.

$x_{1}$ $x_{2}$ $x_{3}$ $s_{1}$ $s_{2}$ $s_{3}$

rhs

ratio

-2 1 -1 0 0 0

$s_{1}$

$s_{2}$

$s_{3}$

3 1 1 1 0 0

1 -1 2 0 1 0

1 1 -1 0 0 1

6/3=2

1/1=1

2/1=2

3.Solving for the New BF Solution

$\bullet$ Create a coefficient 1 for the entering variable in the pivot row by multiplying the row by a suitable number.

$\bullet$ Create a coefficient 0 for the entering variable in all rows except the pivot row by adding a suitable multiple of the pivot row.

$x_{1}$ $x_{2}$ $x_{3}$ $s_{1}$ $s_{2}$ $s_{3}$

rhs

0 -1 3 0 2 0

$x_{1}$

$x_{2}$

$x_{3}$

0 4 -5 1 -3 0

1 -1 2 0 1 0

0 2 -3 0 -1 1

Optimality Test

The coefficient of $x_2$ in row 0 is negative, therefore the current BF solution is NOT optimal.

Iteration 2

$x_{1}$ $x_{2}$ $x_{3}$ $s_{1}$ $s_{2}$ $s_{3}$

rhs

ratio

0 -1 3 0 2 0

$x_{1}$

$x_{2}$

$x_{3}$

0 4 -5 1 -3 0

1 -1 2 0 1 0

0 2 -3 0 -1 1

3/4=3/4

1/2=1/2

$x_{1}$ $x_{2}$ $x_{3}$ $s_{1}$ $s_{2}$ $s_{3}$

rhs

0 0 3/2 0 3/2 1/2

5/2

$s_{1}$

$x_{1}$

$x_{2}$

0 0 1 1 1 -2

1 0 1/2 0 1/2 1/2

0 1 -3/2 0 -1/2 1/2

3/2

1/2

Optimality Test

Since none of the coefficient in row 0 are negative, the current BF solution is optimal.

The optimal BF solution is $(x_{1}^{\ast },x_{2}^{\ast },x_{3}^{\ast },s_{1}^{\ast },s_{2}^{\ast },s^{\ast }_{3})=(\frac{3}{2},\frac{1}{2},0,1,0,0)$ , which implies the optimal solution to the original is $(x_{1}^{\ast },x_{2}^{\ast },x_{3}^{\ast })=(\frac{3}{2},\frac{1}{2},0)$ and the corresponding $Z^{\ast }=\frac{5}{2}$ .

原文链接：https://blog.csdn.net/Hundred_Xu/article/details/121611774