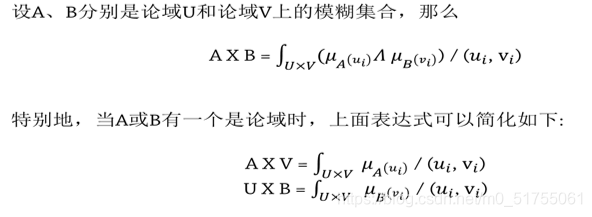目录
学习视频链接
5.5.1 模糊数学的基本知识
模糊推理是利用模糊性知识进行的一种不确定性推理,
研究的事件本身有明确而确定的含义,只是由于发生的条件不充分,使得在条件与事件之间不能出现确定的因果关系,从而在事件的出现与否上表现出不确定性。
在人工智能的应用领域中,知识及信息的不确定性大多是由模糊性引起的,这就使得对模糊推理的研究显得格外重要。
论域:所讨论的全体对象,用 U 等表示。
元素:论域中的每个对象,常用a,b,c,x,y,z表示。
集合:论域中具有某种相同属性的、确定的、可以彼此区别的元素的全体,常用A,B等表示。
- 元素a和集合A的关系:a属于A或a不属于A,即只有两个真值 “真”和“假”。
模糊逻辑给集合中每一个元素赋予一个介于0和1之间的实数, 描述其属于一个集合的强度,该实数称为元素属于一个集合的隶属度。集合中所有元素的隶属度全体构成集合的隶属函数。
(1):模糊集合
隶属度:集合元素对集合的隶属程度
模糊集合相等
模糊集合的包含
模糊集合的并、交、补集
A 并 B:取隶属度的最大值
A 交 B:取隶属度的最小值
补集:1-隶属度
举例(例题)
模糊集合的积
公式理解:用来计算两个集合中元素隶属度的析取,也就是求最小值的过程
(2):模糊关系及运算
模糊关系
- 一个论域到另一个论域
- 举例理解:
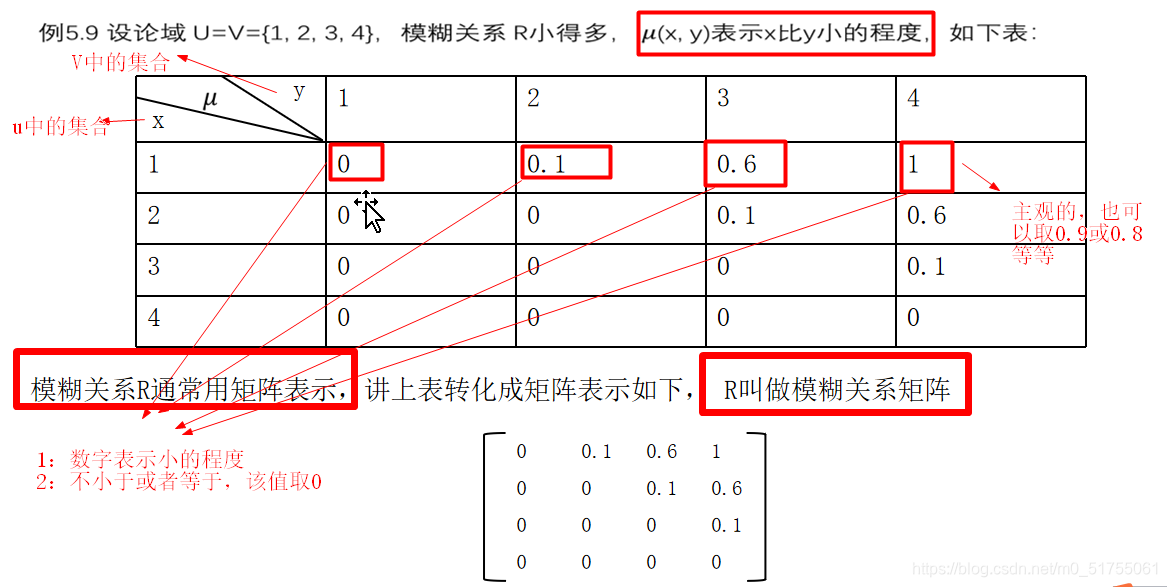
论域u到论域V的模糊关系R
模糊关系的合成
举例:
5.5.2 模糊假言推理
模糊知识的表示
产生式规则(知识)、证据、接近程度
接近程度的计算:
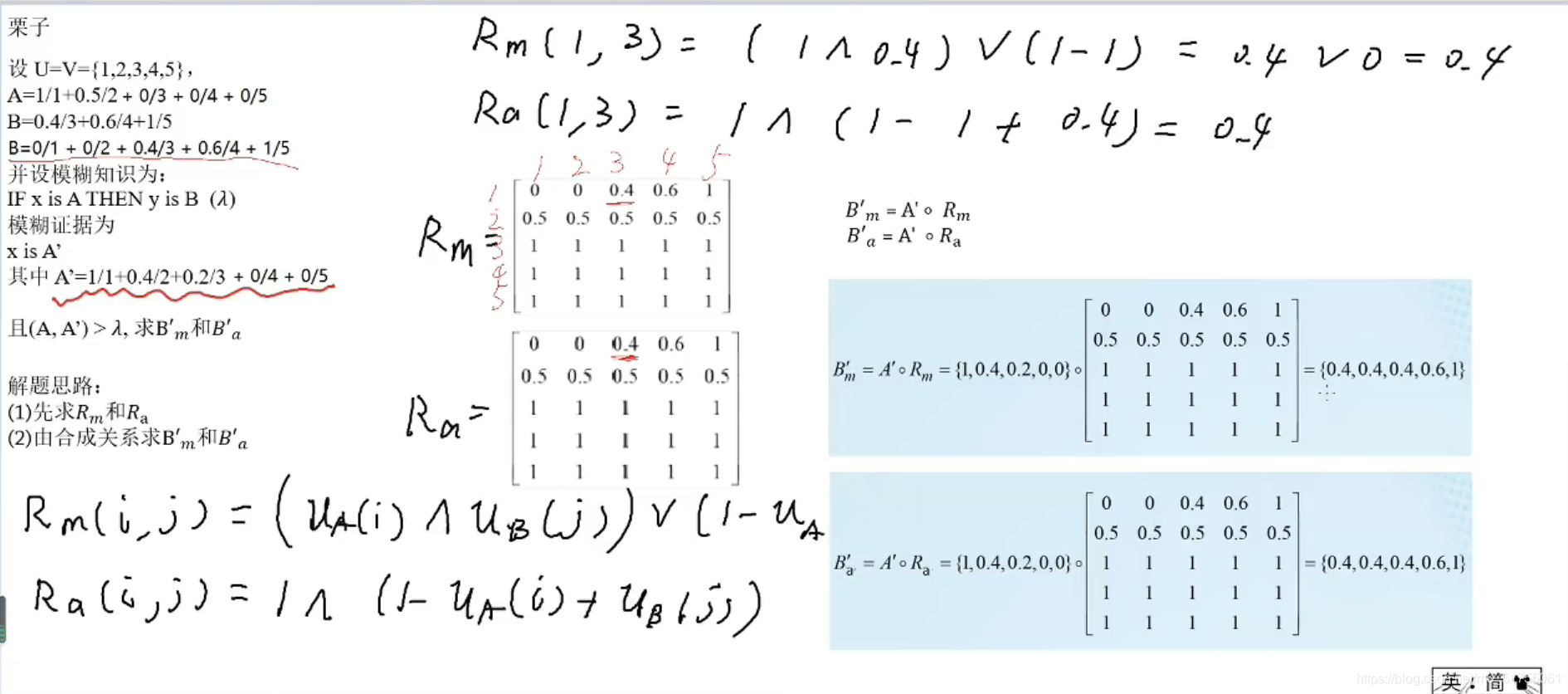
举例:
简单的模糊推理(没懂!!!)
版权声明:本文为m0_51755061原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。