23王道数据结构代码题全解（五）

计划更新23王道数据结构所有课后代码习题的实现，虽然考试写的一般都是伪代码，但是强迫症的我还是全部实现了一遍，仓库在这里

代码全部是用 C++ 写的，都可以编译运行，包含暴力解和最优解。

持续更新，目前更新进度：

• 线性表 14/14
• 链表 25/25
• 栈
• …

仅供参考！ 会包含一些考试不让写的语法，可能也会有一些错误。

18

• 循环单链表结构体及创建函数（可跳过）

// 创建一个带头结点的循环单链表
LinkList createHeadList(vector<int> data) {
  if (data.size() == 0) return NULL;

  LNode* head = (LinkList)malloc(sizeof(LNode));
  head->next = NULL;

  LNode* p = head;
  for (int i = 0; i < data.size(); i++) {
    LNode* q = (LNode*)malloc(sizeof(LNode));
    q->data = data[i];
    q->next = NULL;
    p->next = q;
    p = q;
  }

  p->next = head;  // 最后指向头指针
  return head;
}

void printList(LinkList L) {
  LNode *head = L->next;
  while (head != L) {
    cout << head->data << " ";
    head = head->next;
  }
  puts("");
}

• 首先找到h1的尾结点
• 然后找到h2的尾结点指向h1头结点
• 时间复杂度O(len1+len2)，也就是O(n)，空间复杂度O(1)

void linkTwoLists(LinkList h1, LinkList h2) {
  // 1.创建工作指针
  LNode *p1 = h1->next, *p2 = h2->next;

  // 2.找到h1的尾结点
  while (p1->next != h1) {
    p1 = p1->next;
  }
  
  // 3.链接h2
  p1->next = p2;

  // 4.找到h2的尾结点，指向h1
  while(p2->next != h2) {
    p2 = p2->next;
  }
  p2->next = h1;
}

19

• 遍历循环单链表，每循环一次查找一个最小结点（循环单链表，注意循环终止条件！）
• minp指向最小值结点，minpre指向其前驱
• 输出其值然后删除，循环结束后释放头结点
• 时间复杂度O(n²)，空间复杂度O(1)

void delMin(LinkList L) {
  // 1.创建工作指针，遍历
  LNode *p, *pre, *minp, *minpre;
  while (L->next != L) {
    pre = L, p = L->next;
    minpre = pre, minp = p;
    
    // 2.找到最小值，记录其前缀
    while (p != L) {
      if (p->data < minp->data) {
        minp = p;
        minpre = pre;
      }
      pre = p;
      p = p->next;
    }

    // 3.输出并释放最小值结点
    cout << minp->data << ' ';
    minpre->next = minp->next;
    free(minp);
  }
  
  // 4.释放头结点
  free(L);
}

• 每次删除最小值结点，我们只需要记录最小值前缀即可
• 每次都用 minpre->next 进行比较
• 时间复杂度O(n²)，空间复杂度O(1)

void delMin2(LinkList L) {
  // 1.只剩一个头结点时停止
  while (L->next != L) {
    LNode *minpre = L, *p = L->next;
    
    // 2.找到最小值，记录其前缀
    while (p->next != L) {
      if (p->next->data < minpre->next->data)
        minpre = p;
      p = p->next;
    }
    
    // 3.输出并释放最小值结点
    cout << minpre->next->data << ' ';
    LNode *del = minpre->next;
    minpre->next = del->next;
    free(del);
  }

  // 4.释放头结点
  free(L);
}

• 如果只考虑输出的话，有一个取巧的方法
• 我们把链表的值取出来放在一个数组中排序输出
• 最后释放链表空间即可
• 用了cpp的 sort() ，所以时间复杂度O(nlog₂n)，空间复杂度O(n)

int getLength(LinkList L) {
  int i = 0;
  LNode *p = L->next;
  while (p != L) {
    p = p->next;
    i++;
  }
  return i;
}

void delMin3(LinkList L) {
  int len = getLength(L);
  int a[len], i = 0;

  LNode *head = L->next;
  while (head != L) {
    a[i++] = head->data;
    head = head->next;
  }

  sort(a, a+len);

  for (int i = 0; i < len; i++)
    cout << a[i] << ' ';
  puts("");

  // 释放所有结点空间，此处省略
}

20

• 题中要求结构体及创建函数
• 需要在插入结点时将freq初始化为0

#define ElemType int
typedef struct DNode{
  ElemType data;
  struct DNode *pred, *next;
  int freq;
}DNode, *DLinkList; 

// 创建一个带头结点的非循环双链表 DoublyLinkedList
DLinkList createDlist(vector<int> data) {
  if (data.size() == 0) return NULL;

  DNode* head = (DLinkList)malloc(sizeof(DNode));
  head->next = NULL;

  DNode* p = head;
  for (int i = 0; i < data.size(); i++) {
    DNode* q = (DNode*)malloc(sizeof(DNode));
    q->data = data[i];
    q->freq = 0;     // 初始化
    q->next = NULL;
    q->pred = p;     // 前驱
    p->next = q;
    p = q;
  }

  return head;
}

void printList(DLinkList L) {
  DNode *head = L->next;
  while (head != NULL) {
    cout << head->data << " ";
    head = head->next;
  }
  puts("");
}

• 找到值为x的结点，取下来
• 如果该结点是第一个元素或者freq小于前驱结点，直接返回即可
• 顺着该结点的前驱向前找到第一个freq大于自己的结点，插到它后面
• 最后返回该结点的地址，即指针
• 双链表插入删除一定要注意空结点位置
• 时间复杂度O(n)，空间复杂度O(1)

DNode* locate(DLinkList L, int x) {
  DNode *p = L->next, *q;

  // 1.找到值为x的结点
  while (p != NULL && p->data != x) p = p->next;

  // 2.不存在返回空指针
  if (p == NULL) return NULL;
  else {
    // 3.找到该结点时，freq+1
    p->freq++;

    // 4.是第一个元素（freq已经是最大的了）或是freq小于前驱，直接返回
    if (p->pred == L || p->pred->freq > p->freq) return p;

    // 5.取下该结点
    if (p->next != NULL) p->next->pred = p->pred;
    p->pred->next = p->next;

    // 6.顺着该结点的前驱向前找到第一个freq大于它的结点
    q = p->pred;
    while (q != L && q->freq <= p->freq) q = q->pred;
  
    // 7.找到后插入
    p->next = q->next;
    if (q->next != NULL) q->next->pred = p;
    p->pred = q;
    q->next = p; 
  }
  return p;
}

21

• 这个题是leetcode上很经典的一道链表题

• 看到环我们就要想到快慢指针

• 两个指针，一个fast每次走两步，一个slow每次走一步

• 如果有环的话，fast一定会先进入环，slow后进入环，两个指针都进入环后继续循环一定会相遇

• 同理，相遇则证明环存在，此题已经解决

• 时间复杂度O(n)，空间复杂度O(1)

• 当然你也可以采用暴力做法，遍历然后记录每个出现的结点，如果结点再次出现，则证明有环。这样的时间复杂度为O(n)，空间复杂度也是O(n)

bool isLoop(LNode *head) {
  // 1.快慢指针，快的一次走两步
  LNode *fast = head, *slow = head;
  while (fast != NULL && fast->next != NULL) {
    slow = slow->next;
    fast = fast->next->next;
    if (slow == fast) break;  // 两指针相遇
  }

  // 2.没有环的情况
  if (slow == NULL || fast->next == NULL) {
    return false;
  }

  return true;
}

• 但是通常要求不会那么简单，一定是让你返回环的入口点
• 涉及到入口点，我们就要来算一道数学题
• 假设环内一共有r个元素，链表头结点到环入口点有a个结点，环入口点到相遇点的距离为x（顺时针），快指针已经绕了n圈
• 则有 a+nr+x = 2(a+x)，解得 a = nr-x
• 因此设置一个指针指向head，一个指向相遇点，同步移动，相遇点即为入口点
• 时间复杂度O(n)，空间复杂度O(1)

LNode* findLoopStart(LNode *head) { 
  // 1.快慢指针，快的一次走两步
  LNode *fast = head, *slow = head;
  while (fast != NULL && fast->next != NULL) {
    slow = slow->next;
    fast = fast->next->next;
    if (slow == fast) break;  // 两指针相遇
  }

  // 2.没有环的情况，返回NULL
  if (slow == NULL || fast->next == NULL) {
    return NULL;
  }

  // 3.两个指针分别指向头结点和相遇点
  LNode *p1 = head, *p2 = slow;
  while(p1 != p2) {
    p1 = p1->next;
    p2 = p2->next;
  }

  return p1;
}

22

• 首先想到暴力方法，先get到链表的长度n
• 然后遍历找到第n-k个结点
• 时间复杂度O(n)，空间复杂度O(1)

int searchK(LinkList L, int k) {
  // 1.获取链表长度n
  int n = 0;
  LNode *p = L->link;
  while (p != NULL) {
    p = p->link;
    n++;
  }

  // 2.没有那么多结点，直接返回0
  if (n < k) return 0; 

  // 3.遍历找到第n-k个结点
  int count = n - k;
  p = L->link;
  while (count--) {
    p = p->link;
  }
  cout << "倒数第" << k << "个结点值为" << p->data << endl;
  return 1;
}

• 最优肯定要一次遍历解决，自然而然想到双指针也是快慢指针
• 既然要找到第n-k个结点，我们可以先让前一个指针走k步
• 然后两个指针同步走，等到前一个指针走到结尾，后一个指针自然就走到了n-k结点处
• 时间复杂度O(n)，空间复杂度O(1)

int searchK2(LinkList L, int k) {
  // 1.双指针
  LNode *p1 = L->link, *p2 = L->link;

  int count = 0;
  while (p1 != NULL) {
    if (count < k) count++;
    else p2 = p2->link;   // 2.p1走了k步之后，开始同步走

    p1 = p1->link;      // 3.一直走到链表尾
  }

  // 3.查找成功就输出并返回1
  if (count < k) return 0;
  else {
    cout << "倒数第" << k << "个结点值为" << p2->data << endl;
    return 1;
  }
}

• 当然也有一些其他的奇淫巧计
• 在我们学了栈之后，利用它的“后进先出”的特性，先把所有值压入栈中，再弹出k个元素，最后一个出栈元素即所求值
• 如果你对递归足够了解，你也可以尝试使用递归解决这个问题
• 终止条件就是遍历结点为空，触底反弹，往回走的过程中记录走过的结点，达到k就是倒数第k个结点，直接返回即可
• 如果没有达到k，直接返回NULL即可

23

• 跟第8题基本一样，经典双指针
• 我们可以先让表尾对齐, 比如 loading 和 being 要让str1指向a，str2指向b
• 然后同步遍历即可，两个指针指向同一个结点即共同后缀
• 时间复杂度O(max(len1, len2))，也算O(n)吧，空间复杂度O(1)

int getLen(LinkList L) {
  int len = 0;
  while (L->next != NULL) {
    L = L->next;
    len++;
  }
  return len;
}

// A即str1, B即str2
LNode* findCommon(LinkList A, LinkList B) {
  // 1.计算A, B的长度
  int lenA = getLen(A), lenB = getLen(B);

  // 2.让A, B的长度差距为0
  if (lenA > lenB) {
    for (int i = 0; i < lenA - lenB; i++)
      A = A->next;
  } else {
    for (int i = 0; i < lenB - lenA; i++)
      B = B->next;
  }

  // 3.开始比较
  while (A != NULL) {
    if (A == B)
      return A;
    A = A->next;
    B = B->next;
  }

  // 4.没找到返回NULL
  return NULL;
}

• 当然它是有暴力做法的，你可以使用双重循环，遍历第一个链表的结点的同时遍历第二个链表所有的结点，找到相同点
• 时间复杂度O(len1×len2)，空间复杂度O(1)

LNode* findCommon2(LinkList A, LinkList B) {
  LNode *pa = A->next, *pb = B->next;
  while (pa != NULL) {
    while (pb != NULL) {
      if (pa == pb) 
        return pa;
      pb = pb->next;
    }
    pa = pa->next;
    pb = B->next;   // 重置指针
  }
  return NULL;  // 没找到返回NULL
}

• 这道题想要运行，我们需要稍微改变一下结构体形式以及其他函数（可跳过）

#include <bits/stdc++.h>
#define ElemType char
using namespace std;

typedef struct LNode{
  ElemType data;
  struct LNode* next;
}LNode, *LinkList; 

LinkList createHeadList(vector<ElemType> data) {
  if (data.size() == 0) return NULL;

  LNode* head = (LinkList)malloc(sizeof(LNode));
  head->next = NULL;

  LNode* p = head;
  for (int i = 0; i < data.size(); i++) {
    LNode* q = (LNode*)malloc(sizeof(LNode));
    q->data = data[i];
    q->next = NULL;
    p->next = q;
    p = q;
  }
  return head;
}

void printList(LinkList L) {
  while (L != NULL) {
    cout << L->data;
    L = L->next;
  }
  puts("");
}

int main() {
  vector<char> dataA{'l', 'o', 'a', 'd'};
  vector<char> dataB{'b', 'e'};
  vector<char> dataC{'i', 'n', 'g'};
  LinkList headA = createHeadList(dataA);
  LinkList headB = createHeadList(dataB);
  LinkList headC = createHeadList(dataC);

  LNode *p1 = headA->next, *p2 = headB->next, *p3 = headC->next;
  while (p1->next != NULL) p1 = p1->next;
  while (p2->next != NULL) p2 = p2->next;
  p1->next = p3;
  p2->next = p3;

  cout << "链表A: ";
  printList(headA->next);
  cout << "链表B: ";
  printList(headB->next);
  return 0;  
}

24

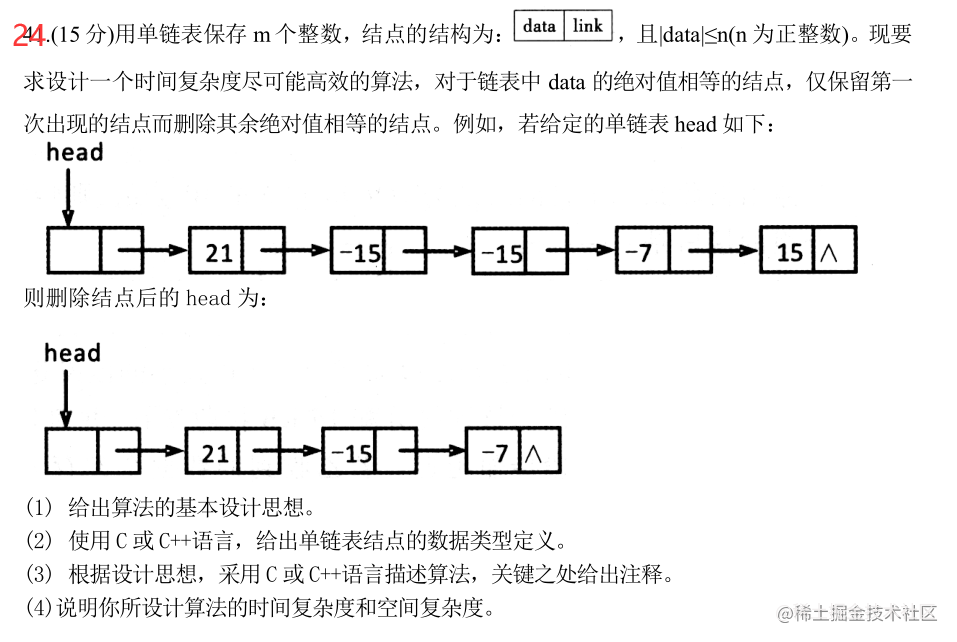
• 首先给出单链表结点的数据类型定义：

typedef struct LNode{
  int data;
  struct LNode* link;
}LNode, *LinkList; 

• 一眼桶排，之前做过很多次这样的题，其实就是用一个辅助数组记录出现过的结点值
• 其实就是把出现的结点值看作数组下标，如果需要记录次数则数组元素代表出现次数
• 第一个数为21，则令辅助数组 arr[21]=1 即可
• 因为 |data| <= n，只需要保存绝对值，所以申请一个大小为 n+1 的辅助数组就可以了
• 我们可以一边遍历，一边判断结点元素值的绝对值是否是第一次出现，不是则删除该结点
• 典型的拿空间换时间，时间复杂度O(m)，空间复杂度O(n)

void delSameAbsoluteValue(LinkList L, int n) {
  // 1.初始化辅助数组
  int arr[n+1] = {0};
  LNode *p = L, *del;

  // 2.遍历同时判别
  while (p->link != NULL) {
    int m = abs(p->link->data);   // 获得绝对值

    if (arr[m] == 0) {
      arr[m] = 1;       // 首次出现
      p = p->link;
    } else {
      del = p->link;    // 非首次出现直接删除
      p->link = del->link;
      free(del);
    }
  }
}

• 有一点需要说明一下
• 408考试的时候，好像是不允许 int arr[n+1] = {0} 这种语法的
• 所以我们需要用 malloc() 来创建数组，然后使用循环或者 memset() 将数组元素初始值置为0
• 注意 memset() 只能将int数组初始化0或-1

int arr[n+1] = {0};

// 推荐写法
int *arr = (int *)malloc(sizeof(int) * (n+1));
for (int i = 0; i < n+1; i++) {
  *(arr+i) = 0;
}

int *arr = (int *)malloc(sizeof(int) * (n+1));
memset(arr, 0, sizeof(int) * (n+1));

int arr[n+1];
memset(arr, 0, sizeof(arr));

25

• 要求时间复杂度O(1)，所以很多取巧暴力的方法就不能用了
• 我们需要把链表均分为两份，然后重新排列，所以需要先找到中间结点
• 链表找中间节点有一种固定使用的方法，就是快慢指针
• 设置两个指针p和q，p每次走一步，q每次走两步
• 当指针q到达链表尾时，p就正好在链表中间（可以自己画一个图，非常好理解）
• 从中间结点断开，分成两个链表
• 然后将后一个链表也就是原链表的后半段进行原地逆置
• 最后分别插入即可
• 时间复杂度O(n)，空间复杂度O(1)

void rearrange(NODE *head) {
  NODE *p = head, *q = head, *tmp, *s;
  
  // 1.快慢指针，找到中间结点
  while(q->next != NULL) {
    p = p->next;
    q = q->next;
    if(q->next != NULL) q = q->next;
  }

  // 2.断链，分成两个链表
  q = p->next;
  p->next = NULL;

  // 3.后一个链表原地逆置，链回去
  while (q != NULL) {
    tmp = q->next;
    q->next = p->next;
    p->next = q;
    q = tmp;
  }

  // 4.拼接两个链表
  s = head->next;
  q = p->next;
  p->next = NULL;

  while (q != NULL) {
    tmp = q->next;
    q->next = s->next;
    s->next = q;
    s = q->next;
    q = tmp;
  }
}

• 思路就是要插入逆置的后半部分的链表，而逆置后半部分就需要先找到中间结点，找中间结点就要用到快慢指针

链表已经更新完毕，5月继续更新栈和队列?‍?