opc r参数 ua_R语言非参时间序列（一）：Metropolis-Hastings算法——不同转移核的思考...

MCMC在金融工程中有着重要作用，它可以用来仿真产品价格分布以及波动，可以用来求解模型中的参数。Metropolis-Hastings算法是一种常用的MCMC算法，本文是我在使用MCMC时候的一些思考，和大家一起分享。阅读本文需要对MCMC有一定的认识，本文默认读者熟悉MCMC，并在此基础上对一些技术细节给出了自己的思考。文中算例采用R语言实现，每一个算例都非常简单，但是很具有代表性，如有不正确的地方，希望大家多多批评，多多指正。

0、Metropolis-Hastings算法回顾

算法的作用，是在已知某种概率密度函数（pdf）的情况下，生成一族服从这种概率密度函数的随机数。这里的概率分布函数应该是比较奇葩的，不然我们也不会用到MH算法。或者，是在已知某种函数的情况下，生成一族随机数，这族随机数的直方图的中点连线就是这个函数。说白了，这个函数就是非正则pdf。我这里说的pdf，可以是连续的，也可以是离散的。

转移核Q：这个转移核的作用可以以某一个概率把i变为j，这个概率我们表示为Q（i，j）。例如某一个转移核能够以3/14的概率把7变成12.8，那么Q（7，12.8）=3/14。如果是离散的转移核，那我们很好理解，它可以是马尔科夫过程，Q就是马氏链的转移矩阵。如果是连续的转移核，那Q就应该是概率密度函数。

仿真目标P：算法的任务是生成一组随机数{

,t=0,1,2,3,4,......}，是的这一组随机数服从某一个我们需要的概率分布，这里P就是我们的目标概率密度函数，它可以是连续的，也可以是离散的。

为了统一符号的需要，本文的Metropolis-Hastings算法（MH算法，henceforth）如下：

Step1：我们需要选取一个转移核Q，这个转移核的作用是输入数A的时候能够以一定的概率变为数B；

Step2：选取一个初始

；

Step3：把

放入转移核Q使得它以某一种概率变为

，这个

到底是什么，我们提前不能知道，也不需要知道，我们只能知道转移出来的结果。我们只需要知道转移核会以某个概率把把

变为

；

Step4：生成一个随机数u~U（0,1），如果

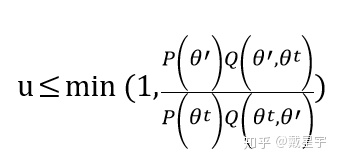
那么

，否则

；

Step5：重复Step3-4，生成大量序列。

1、对（非正则）离散分布仿真，采用随机游走的转移核

假设我们要随机生成的随机变量X，需要满足如下的离散分布：

我们这里使用MH算法，并采用一种随机游走的建议转移核。为什么要使用随机游走的建议转移核？事实上我们用什么核都行，这里我们先使用一种典型转移核，如下：

不带吸收壁的9x9对称马尔科夫随机游走转移矩阵

library(ggplot2)
set.seed(1234)#随机数种子
P<-c(9,1,8,2,7,3,6,4,5)/45#我们的目标概率分布
theta1<-2#初始值
iter<-10000#迭代次数
chain<-vector(length = iter)#要生成的一族随机数
for (i in seq_len(iter)){
  if (theta1==1){
    ifelse(runif(1)<0.5,theta<-theta1,theta<-theta1+1)
  }else if(theta1==11){
    ifelse(runif(1)<0.5,theta<-theta1,theta<-theta1-1)
  }else{
    ifelse(runif(1)<0.5,theta<-theta1+1,theta<-theta1-1)
  }#这个部分其实是转移核Q，对theta1进行转移，Q服从无吸收壁随机游走
  u<-runif(1)
  a<-min(1,P[theta]*0.5/P[theta1]/0.5)#注意：Q(i,j)=0.5,Q(j,i)=0.5
  if (u<a){
    theta1<-theta
  }
  chain[i]<-theta1
}
chain1<-as.data.frame(chain)
ggplot(chain1, aes(x=chain))+
  geom_histogram(bins = 9)#直方图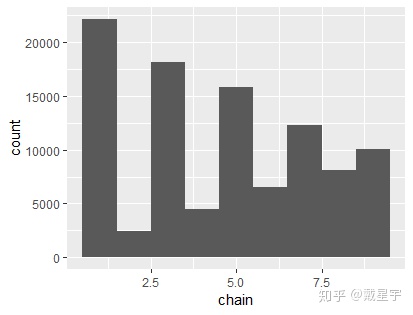

仿真结果

2、对（非正则）离散分布仿真，采用一个很奇怪的转移核（体现出转移核的随意性）

假设我们要随机生成的随机变量X，需要满足如下的离散分布：

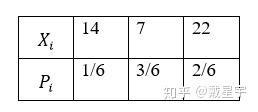
我们说过转移核可以随意选取，到底可以多随意呢？我们不妨采用如下的一个转移核：

瞎编的数字代表我们可以随意找一个转移核

数字是我瞎编的，我们来试一试：

library(ggplot2)
set.seed(1234)
P<-c(1,3,2)/6
theta1<-2#初始值
iter<-100000#迭代次数
Q<-matrix(c(0.234,0.145,0.621,0.66,0,0.34,0.1111,0.2222,0.6667),nr=3,byrow = F)
chain<-vector(length = iter)#要生成的一族随机数
for (i in seq_len(iter)){
  if (theta1==1){
    theta<-sample(c(1:3),prob = c(0.234,0.145,0.621),size = 1)
  }else if(theta1==2){
    theta<-sample(c(1:3),prob = c(0.66,0,0.34),size = 1)
  }else{
    theta<-sample(c(1:3),prob = c(0.1111,0.2222,0.6667),size = 1)
  }#这个部分其实是转移核Q，对theta1进行转移
  u<-runif(1)
  a<-min(1,P[theta]*Q[theta1,theta]/P[theta1]/Q[theta,theta1])
  if (u<a){
    theta1<-theta
  }
  chain[i]<-theta1
}
chain1<-as.data.frame(x1<-c(14,7,22)[chain])
ggplot(chain1, aes(x=x1))+
  geom_histogram(bins = 3)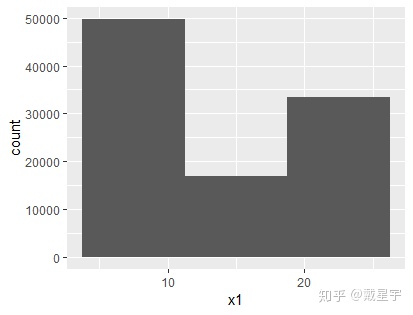

仿真结果

3、对（非正则）离散分布仿真，采用退化转移核（为后面的内容做铺垫）

假设我们要随机生成的随机变量X，需要满足如下的离散分布：

采用退化转移核：

9*9退化转移核

退化转移核作用是对于任意的i,j，Q（i,j）=1/9，我们于是发现一个问题Q(i,j)=Q(j,i)=c了。

library(ggplot2)
set.seed(1234)#随机数种子
P<-c(9,1,8,2,7,3,6,4,5)/45#我们的目标概率分布
theta1<-1#初始值
iter<-10000#迭代次数
chain<-vector(length = iter)#要生成的一族随机数
for (i in seq_len(iter)){
  theta<-sample(1:9,size=1)#这个部分其实是转移核Q，对theta1进行转移
  u<-runif(1)
  a<-min(1,P[theta]/P[theta1])#注意：Q(i,j)=Q(j,i)=c,已经约去
  if (u<a){
    theta1<-theta
  }
  chain[i]<-theta1
}
chain1<-as.data.frame(chain)
ggplot(chain1, aes(x=chain))+
  geom_histogram(bins = 9)#直方图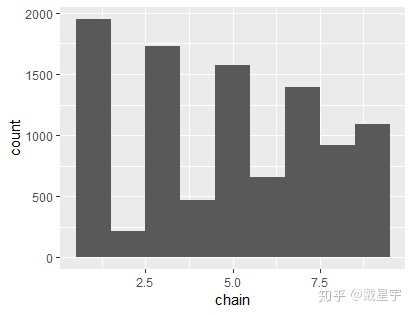

4、对（非正则）连续分布仿真，采用连续转移核

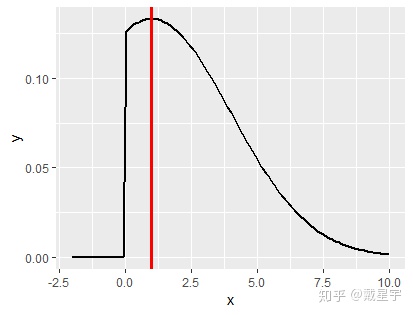
这里才是我们讨论的重点，连续转移核和离散转移核其实是一样的，只不过i和j可以去连续数值而已。举个例子，假如我们现在在处在位置是8.18，假如我们的转移核是连续的，并且是正态分布（均值为8.18，假设标准差为3），那么我们可以计算一下从8.18转移到13的概率Q（8.18,13）=0.4459，也就是说它将以44.59%的概率转移到13，那向左移动到2.22呢？Q（8.18，2.21）=0.023，也就是说它将以2.3%的概率移动到2.21。我们从图上可以感知一下，什么是连续的转移核：

蓝线所在位置是8.18，它将以进行正态分布（标准差假设为3）为转移核进行转移

现在蓝线转移到绿线（x=3）了，我们计算出来Q（8.18,13）=0.4459

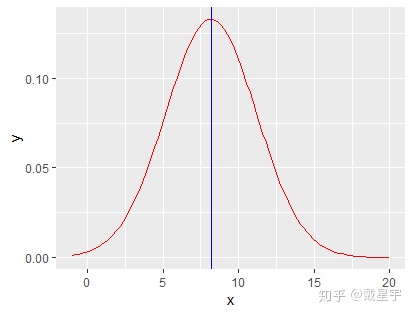
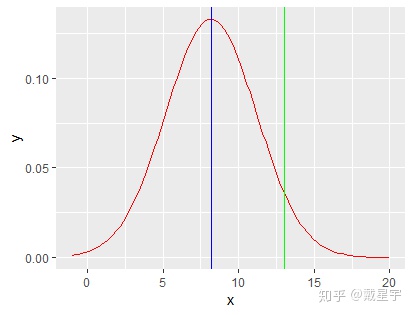
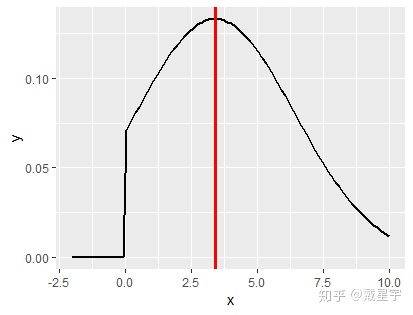
那么我们可以发现转移是对称的，什么叫对称呢，就是Q(i,j)=Q(j,i)，也就是Q（8.18,13）=Q（13,8.18）,我们可以从图上一眼看出来：

从蓝线转移到绿线和从绿线转移到蓝线有着相同的概率分布

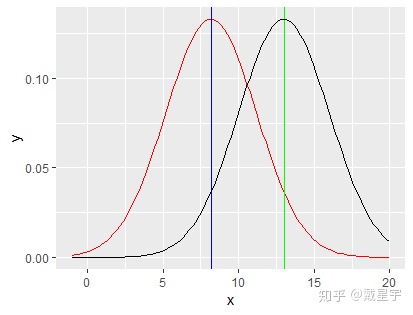
那么我们来试一试：假如我要实现X~

(x＞0）,我们用正态转移核来试一试。我们这里发现一个问题！x只能取大于0的数，所以我们的转移核是截断的，我们不能转移到小于0的地方！什么是截断的转移核呢！就是说我们的转移核长这样（我们假设均值是1）：

我们假设此时我们在位置1（红线），我们采用正态转移核（标准差为3），可是我们不能转移到小于0的的地方，所以我们必须对转移核进行截断！形成一种截断转移核。

我们假设此时我们在位置3.4（红线），我们采用正态转移核（标准差为3），可是我们不能转移到小于0的的地方，所以我们必须对转移核进行截断！形成一种截断转移核。

我们来试一试：

实现X~

(x＞0），采用标准差为3的正态截断转移核。

library(ggplot2)
set.seed(1234)
P<-function(x) 0.5*x^2*exp(-x)
theta1<-rnorm(1,mean = 5)
iter<-20000
chain<-vector(length = iter)
for (i in seq_len(iter)){
  theta<-rnorm(1,mean = theta1)
  if (theta<0){
    theta<-theta1
  }
  u<-runif(1)
  a<-min(P(theta)*dnorm(theta1,mean=theta,sd=3)/(P(theta1)*dnorm(theta1,mean=theta,sd=3)),1)
    theta1<-theta
  }
  chain[i]<-theta1
}
chain1<-as.data.frame(chain)
ggplot(chain1, aes(x=chain))+
  geom_histogram(bins = 100)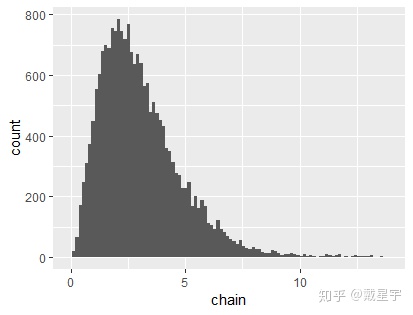

上图是MH结果，下图是真实的pdf

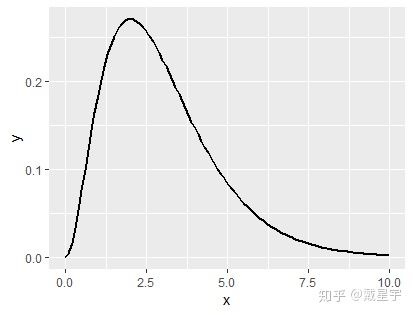
5、对（非正则）连续分布仿真，采用连续退化转移核

5其实就是对3的衍生，退化转移核在连续分布下其实就是均匀分布，但是有一个问题，这个均匀分布的取值范围是什么？我们首先来试一试，取值范围是【x-3,x+3】的情形：

此时，Q(i,j)=Q(j,i)，

library(ggplot2)
set.seed(1234)#随机数种子
P<-function(x) 0.5*x^2*exp(-x)
theta1<-rnorm(1,mean = 5)
iter<-20000
chain<-vector(length = iter)
for (i in seq_len(iter)){
  theta<-runif(1,min = theta1-3,max=theta1+3)
  if (theta<0){
    theta<-theta1
  }
  u<-runif(1)
  a<-min(P(theta)/P(theta1),1)#建议分布是概率密度函数
  if (u<a){
    theta1<-theta
  }
  chain[i]<-theta1
}
chain1<-as.data.frame(chain)
ggplot(chain1, aes(x=chain))+
  geom_histogram(bins = 100)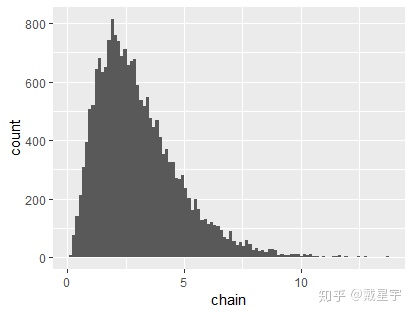

6、对（非正则）连续分布仿真，转移核已经退化，没有转移核了

什么意思？如果5中，我们的均匀分布无限延长就是没有转移核了，我们会取一个大于0的随机点，我们先假设是0到1000，我们先试一试。

library(ggplot2)
set.seed(1234)#随机数种子
P<-function(x) 0.5*x^2*exp(-x)
theta1<-4
iter<-200000
chain<-vector(length = iter)
for (i in seq_len(iter)){
  theta<-runif(1,min =0,max=1000)
  if (theta<0){
    theta<-theta1
  }
  u<-runif(1)
  a<-min(P(theta)/P(theta1),1)#建议分布是概率密度函数
  if (u<a){
    theta1<-theta
  }
  chain[i]<-theta1
}
chain1<-as.data.frame(chain)
ggplot(chain1, aes(x=chain))+
  geom_histogram(bins = 100)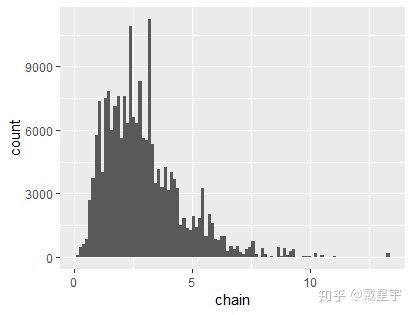

问题出在20万次的仿真对于0,1000这个随机转移区间来说远远不够，也体现出了这种方法效率的低下

有点困了，先写这么多吧。star19950818@foxmail.com。

原文链接：https://blog.csdn.net/weixin_29243279/article/details/112184171