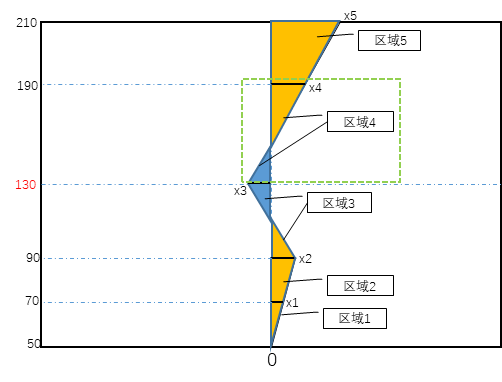
计算下图中折线与y轴围成的面积,蓝色为负,黄色为正,正负抵消后的和。
- 采用梯形面积和累加,
- 由于业务需要,本例以130为边界,分别求50-130之间的面积,以及130-210之间的面积>
本例只给 ( 50 , x 1 ) , ( 70 , x 2 ) , ( 90 , x 3 ) , ( 130 , x 4 ) , ( 190 , x 5 ) , ( 230 , x 6 ) (50, x_1),(70, x_2),(90, x_3),(130, x_4),(190, x_5),(230, x_6)(50,x1),(70,x2),(90,x3),(130,x4),(190,x5),(230,x6),这 6 个点, 其中x 1 = 0 x_1=0x1=0
- 区域1面积: 是一个三角形,为 底*高/2 即为:x 2 × ( 70 − 50 ) ÷ 2 x_2\times{(70-50)\div{2}}x2×(70−50)÷2
- 区域2面积:梯形面积,上底+下底*高/2,即为:( x 1 + x 2 ) × ( 90 − 70 ) ÷ 2 (x_1+x_2)\times{(90-70)\div{2}}(x1+x2)×(90−70)÷2
- 区域3面积:可以直接上底+下底*高/2,(已经过验证),分析过程,蓝色三角形和黄色三角形是相似三角形,。$$
- 首先判断a = ∣ x 2 ∣ − ∣ x 3 ∣ a=\mid x_2 \mid-\mid{x_3}\mida=∣x2∣−∣x3∣的大小,若a > 0 a>0a>0,而且1和2面积正负抵消,剩余就是求3的面积,即梯形3的面积则面积为( x 2 + ∣ x 3 ∣ ) × (x_2+\mid x_3\mid)\times{}(x2+∣x3∣)×
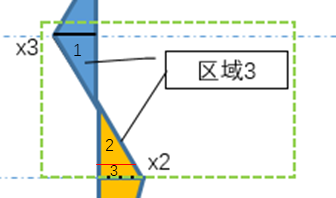
- 首先判断a = ∣ x 2 ∣ − ∣ x 3 ∣ a=\mid x_2 \mid-\mid{x_3}\mida=∣x2∣−∣x3∣的大小,若a > 0 a>0a>0,而且1和2面积正负抵消,剩余就是求3的面积,即梯形3的面积则面积为( x 2 + ∣ x 3 ∣ ) × (x_2+\mid x_3\mid)\times{}(x2+∣x3∣)×
- 区域4,类似1区域3
- 区域5,类似于区域3
复杂写法:
aera['down'] = df_10min_down.apply(lambda x: sum( \
[0.5*(abs(i[0][0])/(abs(i[0][0])+abs(i[0][1])))*i[1]*i[0][0]*(1-(i[0][1]/i[0][0])**2) if i[0][0]*i[0][1] < 0 else 0.5*(i[0][0]+i[0][1])*i[1] \
for i in zip(zip(x[:-1], x[1:]), height[:6])]), axis=1)
aera['up'] = df_10min_up.apply(lambda x: sum( \
[0.5*(abs(i[0][0])/(abs(i[0][0])+abs(i[0][1])))*i[1]*i[0][0]*(1-(i[0][1]/i[0][0])**2) if i[0][0]*i[0][1] < 0 else 0.5*(i[0][0]+i[0][1])*i[1] \
for i in zip(zip(x[:-1], x[1:]), height[6:])]), axis=1)
简化写法(推荐)
aera['down'] = df_10min_down.apply(lambda x: sum([0.5*(i[0][0]+i[0][1])*i[1] for i in zip(zip(x[:-1], x[1:]), height[:6])]), axis=1)
aera['up'] = df_10min_up.apply(lambda x: sum([0.5*(i[0][0]+i[0][1])*i[1] for i in zip(zip(x[:-1], x[1:]), height[6:])]), axis=1)
版权声明:本文为weixin_46713695原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。