动态规划
1.递推算法
例题 位数问题
【问题描述】
在所有的N位数中,有多少个数中有偶数个数字3?由于结果可能很大,你只需要输出这个答案对12345取余的值。
【输入格式】
读入一个数N
【输出格式】
输出有多少个数中有偶数个数字3。
【输入样例】
2
【输出样例】
73
【数据规模】
1<=N<=1000
【样例说明】
在所有的2位数字,包含0个3的数有72个,包含2个3的数有1个,共73个
理解
考虑这种题目,一般来说都是从第i-1位推导第i位,且当前位是取偶数还是取奇数的。
可以用f[i][0]表示前i位有偶数个3的方案数
f[i][1]表示前i位有奇数个3的方案数
则状态转移方程可以表示为:
f[i][0]=f[i-1][0]*9+f[i-1][1];
f[i][1]=f[i-1][0]+f[i-1][1]*9;
边界条件:f[1][1]=1; f[1][0]=8;
例题代码
#include <iostream>
using namespace std;
const int M=12345;//取模
const int N=1000+5; //最多1000位数
int main()
{
//f[i][0]表示前i位有偶数个3的方案数,f[i][1]表示前i位有奇数个3的方案数
int f[N][2],n;
f[1][0]=8;f[1][1]=1;//1位数的情况
cin>>n;
for(int i=2;i<=n;i++){
f[i][0]=(f[i-1][0]*9+f[i-1][1])%M;
f[i][1]=(f[i-1][1]*9+f[i-1][0])%M;
}
cout<<f[n][0]<<endl;
return 0;
}
2.基础dp
算法思想
如果各个子问题不是独立的,如果能够保存已经解决的子问题的答案,而在需要的时候再找出已求得的答案,这样就可以避免大量的重复计算。
基本思路是,用一个表记录所有已解决的子问题的答案,不管该问题以后是否被用到,只要它被计算过,就将其结果填入表中。
求解过程
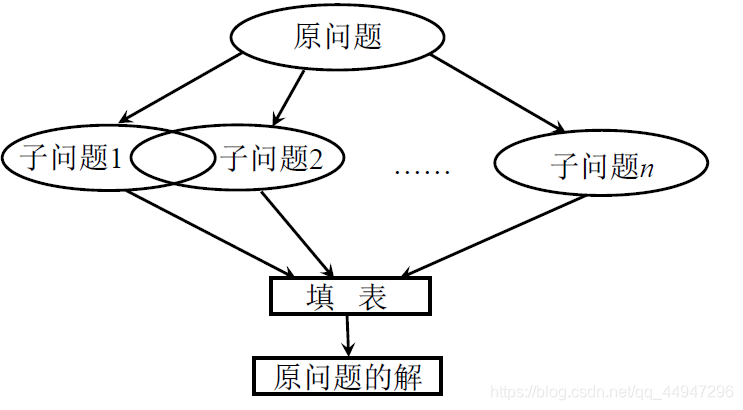
基本步骤
动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值(最大值或最小值)的那个解。
动态规划法设计算法一般分成三个阶段:
(1)分段:将原问题分解为若干个相互重叠的子问题;
(2)分析:分析问题是否满足最优性原理,找出动态规划函数的递推式;
(3)求解:利用递推式自底向上计算,实现动态规划过程。
动态规划法利用问题的最优性原理,以自底向上的方式从子问题的最优解逐步构造出整个问题的最优解。
滚动数组
•处理dp[][]状态数组的时候,有个小技巧:把它变成一维的dp[],以节省空间。
•观察二维表dp[][],可以发现,每一行是从上面一行算出来的,只跟上面一行有关系,跟更前面的行没有关系。
•那么用新的一行覆盖原来的一行就好了。
3.求最长递增子序列
1、暴力法:枚举所有的子序列,判断是不是递增的,如果是递增的求最大值。
2、采用LCS的方法:
1)原序列A排序得到B
2) 求A和B的LCS
3、直接DP
4、借助二分查找,优化为O(nlogn)
dp解法
先确定动态规划的状态,这个问题可以用序列某一项作为结尾来作为一个状态。
用dp[i]表示一定以第i 项为结尾的最长上升子序列。
用a[i] 表示第i 项的值
如果有j < i且a[j] < a[i],那么把第i 项接在第j 项后面构成的子序列长度为:dp[i] = dp[j] + 1。
•要使dp[i] 为以i 结尾的最长上升子序列,需要枚举所有满足条件的j。所以转移方程是: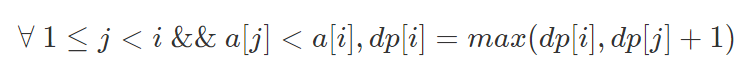
3.递推与记忆化搜索
•前面DP的状态转移,都是用递推的方法。
•有另一种方法,逻辑上的理解更加直接,这就是用“递归+记忆化搜索”来实现DP。
记忆化搜索思想
用递归实现DP时,在递归程序中记录计算过的状态,并在后续的计算中跳过已经算过的重复的状态,从而大大减少递归的计算次数,这就是“记忆化搜索”的思路。
•递归时,有大量重复计算,其实能避免。
•观察第3层的中间数“1”,从第2层的“3”往下走会经过“1”,计算一次从“1”出发的递归;从第2层的“8”往下走会也经过“1”,又重新计算了从“1”出发的递归。所以,只要避免这些重复计算,就能优化。
7(30)
3(23) 8(21)
8(20) 1(13) 0(10)
2(7) 7(12) 4(10) 4(10)
4(4) 5(5) 2(2) 6(6) 5(5)
4.背包问题
1.0/1背包
2.完全背包
3.多重背包
4.混合背包
5.分组背包
6.依赖背包
我认为后面的背包问题都是由0/1背包问题衍生出来,所以把0/1背包问题思想理解透彻才是最根本的
0/1背包
一、定义状态:
a[i][j]:表示容量为j的背包选择前i件物品的最大价值和
二、状态转移方程
1、w[i] > j ,第i件物品太重了,容量为j的背包装不下
a[i][j] = a[i -1][j]
2、w[i] <= j
a[i][j] = max(a[i -1][j],a[i -1][j -w[i]] + v[i]);
理解
在0/1背包问题中,物品i或者被装入背包,或者不被
装入背包,设xi
表示物品i装入背包的情况,
则当xi=0时,表示物品i没有被装入背包,
xi=1时,表示物品i被装入背包。
根据问题的要求,有如下约束条件和目标函数: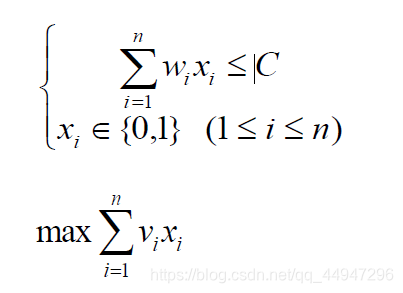
按这样的规律一行行填表,直到结束。现在回头考虑,装了哪些物品。
看最后一列,15>14,说明装了物品5,否则价值不会变化。
#include<bits/stdc++.h>
intn,c;//n件物品,背包容量为c
intw[N],v[N];//重量是w,价值是V
cin>> n >> c;//读入物品数量n和背部的容量c
for(inti= 1;i <= n;i++)//读入每件物品的重量和价值
cin>> w[i] >> v[i];
//用dp方程建表,行表示物品[1,n],列表示背包容量[1,c]
//dp[i]表示容量为i的背包选择物品的最大价值和
intdp[N] = {0};//初始化表为0
//顺序遍历n件物品
for(inti= 1;i <= n;i++){
for(intj = c; j >= w[i]; j--){//背包容量[1,c],从右到左填表
//不选当前物品和选当前物品(背包容量变为j-w[i])两种方案求最大值
dp[j] = max(dp[j],dp[j -w[i]] + v[i]);
}
}
训练例题
数塔问题
题目描述
设有一个三角形的数塔,顶点为根结点,每个结点有一个整数值。从顶点出发,可以向左走或向右走,如图所示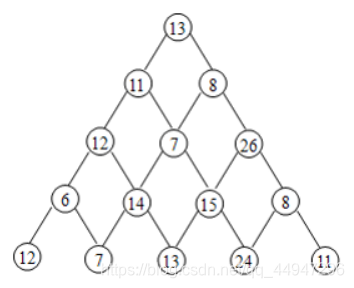
若要求从根结点开始,请找出一条路径,使路径之和最大,只要输出路径的和。
输入
第一行为n(n<10),表示数塔的层数
从第2行至n+1行,每行有若干个数据,表示数塔中的数值
输出
输出路径和最大的路径值。
样例输入
5
13
11 8
12 7 26
6 14 15 8
12 7 13 24 11
样例输出
86
#include<bits/stdc++.h>
using namespace std;
int main()
{
int a[15][15];
int n;
cin >> n;
memset(a,0,sizeof(a));
for(int i = 1;i <= n;i++){
for(int j = 1;j <= i;j++){
cin >> a[i][j];
}
}
for(int i=n;i>=1;i--){
for(int j =1;j <=n;j++){
a[i][j] = max(a[i+1][j],a[i+1][j+1])+a[i][j];
}
}
cout <<a[1][1]<<endl;
return 0;
}
昆虫繁殖
题目描述
科学家在热带森林中发现了一种特殊的昆虫,这种昆虫的繁殖能力很强。每对成虫过x个月产y对卵,每对卵要过两个月长成成虫。假设每个成虫不死,第一个月只有一对成虫,且卵长成成虫后的第一个月不产卵(过X个月产卵),问过Z个月以后,共有成虫多少对?0≤X≤20,1≤Y≤20,X≤Z≤50
输入
x,y,z的数值
输出
过Z个月以后,共有成虫对数
样例输入
1 2 8
样例输出
37
#include<bits/stdc++.h>
using namespace std;
int main()
{
int x,y,z,a[55];
cin >> x >> y >> z;
for(int i = 0;i <= x+2;i++ ) a[i] = 1;
for(int i = x + 2;i <=z;i++){
a[i] = a[i-x-2] * y+ a[i-1];
}
cout << a[z];
return 0;
}
走楼梯
题目描述
楼梯有n级台阶,上楼可以一步上一阶,也可以一步上二阶。编一程序,计算共有多少种不同走法?
本题要求用递归算法实现。
输入
输入n(n<=50)
输出
输出走法的总数。
样例输入
3
样例输出
3
#include<bits/stdc++.h>
using namespace std;
int f(int n)
{
if(n < 1)
return 0;
if(n == 1)
return 1;
if(n == 2)
return 2;
return f(n-1) + f(n-2);
}
int main(){
int n;
cin >> n;
cout << f(n) << endl;
}
兔子繁殖
题目描述
有一种兔子,出生后一个月就可以长大,然后再过一个月一对长大的兔子就可以生育一对小兔子且以后每个月都能生育一对。现在,我们有一对刚出生的这种兔子,那么,n个月过后,我们会有多少对兔子呢?假设所有的兔子都不会死亡。
输入
输入仅一行,包含一个自然数n(n≤40)。
输出
输出仅一行,包含一个自然数,即n个月后兔子的对数。
样例输入
5
样例输出
5
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n,s1,s2,t;
cin >> n;
if(n < 3)
cout << "1" << endl;
else
{
s1=1,s2=1;
for(int i = 3;i <= n;i++){
s1 =s1 + s2;
t = s1;
s1 = s2;
s2 = t;
}
cout << s2 << endl;
}
return 0;
}
平面分割
题目描述
同一平面内有N(n≤500)条直线,已知其中P(p≥2)条直线相交于同一点,则这Ñ条直线最多能将平面分割成多少个不同的区域?
输入
两个整数N(n≤500)和P(2≤p≤n)
输出
一个正整数,代表最多分割成的区域数目
样例输入
12 5
样例输出
73
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n,m;
cin >> n >> m;
int t = 2 * m;
for(int i = m+1;i<=n;i++)
t+=i;
cout << t << endl;
return 0;
}
0/1背包
题目描述
一个旅行者有一个最多能用m公斤的背包,现在有n件物品,它们的重量分别是W 1,W 2,…,W n,它们的价值分别为C 1,C 2, … 。,C n。若每种物品只有一件求旅行者能获得最大总价值。
输入
第1行:两个整数,M(背包容量中,M <= 200)和N(物品数量,N <= 30);
第2…N + 1行:每行二个整数W i,C i,表示每个物品的重量和价值。
输出
仅一行,一个数,表示最大总价值。
样例输入
10 4
2 1
3 3
4 5
7 9
样例输出
12
#include<bits/stdc++.h>
using namespace std;
const int N = 210;
int main()
{
int n,m;
int w[N],v[N]; // 重量w,价值v
cin >> m >> n; //背包的容量c 读入物品的数量
for(int i = 1;i <= n;i++){
cin >> w[i] >> v[i]; //读入物品的重量和价值
}
//用dp方程建表
int dp[N]= {0};
//顺序遍历n件物品
for(int i = 1;i <= n;i++){
for(int j = m;j >= w[i];j--){
if(dp[j] < dp[j-w[i]]+v[i])
dp[j] = dp[j-w[i]]+v[i];
}
}
cout << dp[m]<< endl;
return 0;
}
采药问题
题目描述
辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是辰辰,你能完成这个任务吗?
输入
输入的第一行有两个整数T(1 <= T <= 1000)和M(1 <= M <= 100),用一个空格隔开,T代表总共能够用来采药的时间,M代表山洞里的草药的数目。接下来的M行每行包括两个在1到100之间(包括1和100)的整数,分别表示采摘某株草药的时间和这株草药的价值。
输出
输出包括一行,这一行只包含一个整数,表示在规定的时间内,可以采到的草药的最大总价值。
样例输入
70 3
71 100
69 1
1 2
样例输出
3
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int main()
{
int n,m;
int w[N],v[N]; // 重量w,价值v
cin >> m >> n; //背包的容量c 读入物品的数量
for(int i = 1;i <= n;i++){
cin >> w[i] >> v[i]; //读入物品的重量和价值
}
//用dp方程建表
int dp[N]= {0};
//顺序遍历n件物品
for(int i = 1;i <= n;i++){
for(int j = m;j >= w[i];j--){
if(dp[j] < dp[j-w[i]]+v[i])
dp[j] = dp[j-w[i]]+v[i];
}
}
cout << dp[m]<< endl;
return 0;
}
搬寝室
题目描述
搬寝室是很累的,xhd深有体会.时间追述2006年7月9号,那天xhd迫于无奈要从27号楼搬到3号楼,因为10号要封楼了.看着寝室里的n件物品,xhd开始发呆,因为n是一个小于2000的整数,实在是太多了,于是xhd决定随便搬2k件过去就行了.但还是会很累,因为2k也不小是一个不大于n的整数.幸运的是xhd根据多年的搬东西的经验发现每搬一次的疲劳度是和左右手的物品的重量差的平方成正比(这里补充一句,xhd每次搬两件东西,左手一件右手一件).例如xhd左手拿重量为3的物品,右手拿重量为6的物品,则他搬完这次的疲劳度为(6-3)^2 = 9.现在可怜的xhd希望知道搬完这2*k件物品后的最佳状态是怎样的(也就是最低的疲劳度),请告诉他吧。
输入
每组输入数据有两行,第一行有两个数n,k(2<=2*k<=n<2000).第二行有n个整数分别表示n件物品的重量(重量是一个小于2^15的正整数).
输出
对应每组输入数据,输出数据只有一个表示他的最少的疲劳度,每个一行.
样例输入
5 1
18467 6334 26500 19169 15724
7 1
29358 26962 24464 5705 28145 23281 16827
0 0
样例输出
492804
1399489
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2005;
const int INF = 0x3f3f3f3f;
int w[maxn];
int dp[maxn][maxn];
int main()
{
int n,k;
while(cin>>n>>k)
{
if(n == 0&&k==0) return 0;
for(int i = 1;i <= n;i++){
cin >> w[i];
}
sort(w+1,w+n+1);
memset(dp,INF,sizeof(dp));
for(int i = 0;i <= n;i++){
dp[0][i] = 0;
}
for(int i = 1;i <= k;i++){
for(int j = 2;j <= n;j++){
dp[i][j] = min(dp[i][j-1],dp[i-1][j-2] + (w[j]-w[j-1])*(w[j]-w[j-1]));
}
}
cout << dp[k][n] << endl;
}
return 0;
}
机器分配
题目描述
总公司拥有高效设备M台,准备分给下属的N个分公司。各分公司若获得这些设备,可以为国家提供一定的盈利。问:如何分配这M台设备才能使国家得到的盈利最大?求出最大盈利值。其中M≤15,N≤10。分配原则:每个公司有权获得任意数目的设备,但总台数不超过设备数M。
输入
输入数据文件格式为:第一行有两个数,第一个数是分公司数N,第二个数是设备台数M。
接下来是一个N*M的矩阵,表明了第 I个公司分配 J台机器的盈利。
输出
输出有多行。
第1行输出最大盈利值;
第2行到第n+1行输出第1到第n家分公司的分配情况。每行有2个整数,用空格隔开,分别表示分公司的编号和分配的设备数。
样例输入
3 3
30 40 50
20 30 50
20 25 30
样例输出
70
1 1
2 1
3 1
#include<bits/stdc++.h>
using namespace std;
void outp(int x,int num);
int a[20][20];
int dp[25][25];
int main()
{
int n,m;
cin >> n >> m;
memset(dp,0,sizeof(dp));
memset(a,0,sizeof(a));
for(int i = 1;i <= n;i++)
for(int j = 1;j <= m;j++){
cin >> a[i][j];
}
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
for(int k = 0;k <= j;k++){
dp[i][j] = max(dp[i-1][k]+a[i][j-k],dp[i][j]);
}
}
}
cout << dp[n][m] << endl;
outp(n,m);
}
void outp(int x,int num)
{
if (x==0)
return;
for (int i=0;i<=num;i++)
if (dp[x][num]==dp[x-1][i]+a[x][num-i])
{
outp(x-1,i);
cout<<x<<' '<<num-i<<endl;
break;
}
return;
}
Bone Collector
题目描述
Many years ago , in Teddy’s hometown there was a man who was called “Bone Collector”. This man like to collect varies of bones , such as dog’s , cow’s , also he went to the grave …
The bone collector had a big bag with a volume of V ,and along his trip of collecting there are a lot of bones , obviously , different bone has different value and different volume, now given the each bone’s value along his trip , can you calculate out the maximum of the total value the bone collector can get ?
输入
The first line contain a integer T , the number of cases.
Followed by T cases , each case three lines , the first line contain two integer N , V, (N <= 1000 , V <= 1000 )representing the number of bones and the volume of his bag. And the second line contain N integers representing the value of each bone. The third line contain N integers representing the volume of each bone.
输出
One integer per line representing the maximum of the total value (this number will be less than 2 31).
样例输入
1
5 10
1 2 3 4 5
5 4 3 2 1
样例输出
14
#include<bits/stdc++.h>
using namespace std;
int dp[1008][1008];
int value[1008];
int vol[1008];
int max(int a,int b)
{
return a>b?a:b;
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n,v;
memset(dp,0,sizeof(dp));
scanf("%d%d",&n,&v);
for(int i=1;i<=n;i++)
{
scanf("%d",&value[i]);
}
for(int i=1;i<=n;i++)
{
scanf("%d",&vol[i]);
}
for(int i=1;i<=n;i++)//石头个数
{
for(int j=0;j<=v;j++)//背包体积不断变大
{
dp[i][j]=dp[i-1][j];
if(j>=vol[i])
{
dp[i][j]=max(dp[i][j],dp[i-1][j-vol[i]]+value[i]);
}
}
}
cout<<dp[n][v]<<endl;
}
return 0;
}