算法学习之减治法
文章目录
减治法的基本思想
- 将规模为n的问题递减为规模为n-1或n/2的子问题,反复递减后对子问题分别求解,再建立子问题的解与原问题的解的关系。
- 减治法有三个变形:
- 减常数(如1) :每此迭代规模减小n→n-1
- 减因子(如1/2):每此迭代规模减半n→ n/2
- 减可变规模:每此迭代减小的规模不同
插入排序
- 插入排序的过程类似玩牌时整理手中纸牌的过程。它的基本思想是:每步将一个待排序的对象按照其关键字的大小,插到前面已经排好序的序列中的适当位置,直到全部对象插入完毕为止。
- 常用的插入排序有:直接插入排序、折半插入排序、链表插入排序和希尔排序,它们划分的依据是在排好序的序列中寻找插入位置所使用方法的不同。
直接插入排序举例
待排序序列{89,45,68,90,29,34,17}
插入过程:
{89} 不需比较
{45,89}
{45,68,89}
{45,68, 89,90}
{29,45,68, 89,90}
{29,34,45,68 89, 90}
{17,29,34,45,68, 89, 90}
插入次数=n-1=6
直接插入排序伪代码
ALGORITHM InsertionSort( A[0..n-1] )
// 对给定序列进行直接插入排序
// 输入:大小为n的无序序列A
// 输出:按非递减排列的序列A
for i ← 1 to n-1 do
v ← A[i]
j ← i-1
while j ≥ 0 and A[j] > v do
A[j+1] ← A[j]
j ← j –1
A[j+1] ←v
直接插入排序效率分析
基本操作: 比较
比较次数C(n):
最坏的情形,每次插入需比较已插入的所有元素,此时,第i次插入比较i个元素,故
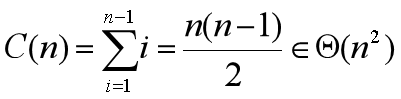
深度优先
可以从任何顶点开始访问图的顶点,每次迭代时,处理与当前顶点相邻的未访问顶点。
用栈来跟踪深度优先查找的操作最方便。
DFS的伪代码
Pseudocode for Depth-first-search of graph G=(V,E):
DFS(G)
count :=0
未访问的顶点标记为 0
for each vertex v∈ V do
if v 的标记为 0
dfs(v)
dfs(v)
count := count + 1
顶点 v 标记为 count
for each vertex w adjacent to v do
if w is marked with 0
dfs(w)
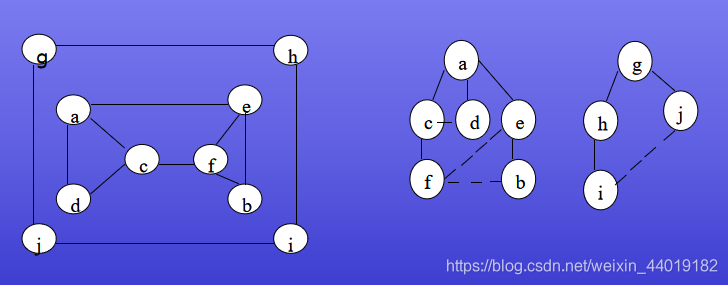
深度优先举例
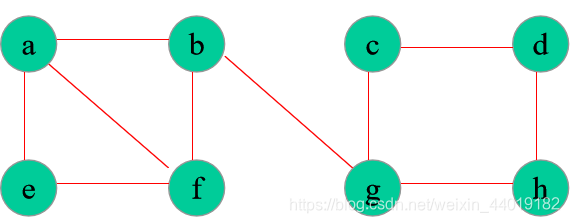
一个DFS输出序列:
a-b-g-c-d-h-f-e
深度优先搜索的效率与图的表示有关
对邻接矩阵表示的图:
遍历的效率为
Θ(| V |^2)
对邻接链表表示的图:
遍历的效率为
Θ(| V |+| E |)
构造深度优先查找森林:遍历的初始顶点作为这样深度优先查找森林中第一颗树的根。无论何时,如果第一次遇到一个新的未访问顶点,它是从哪个顶点被访问到,就把它附加为哪个顶点的子女。连接这样两个顶点的边称为树向边。该算法也可能会遇到一条指向已访问顶点的边,并且这个顶点不是它的直接前趋(即它在树中的父母),我们把这种边称为回边。
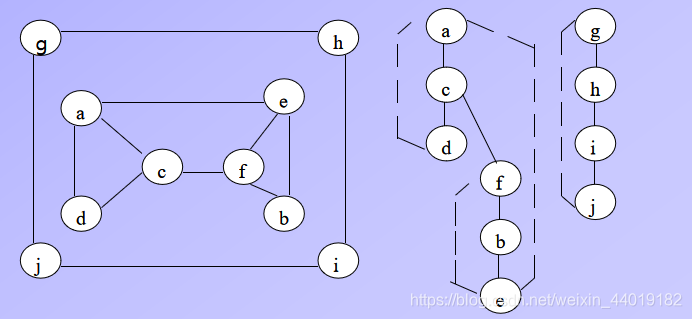
- 注意,DFS产生两种顶点序列:第一次访问顶点的次序(入栈)和顶点成为死端的次序(出栈)
- DFS重要的基本应用包括检查图的连通性和无环性。
- 检查一个图的连通性:从任意一个顶点开始DFS遍历,在该算法停下来以后,检查一下是否所有的顶点都被访问过了。如果都访问过了,那个这个图是连通的;否则,它是不连通的。
- 检查一个图中是否包含回路:如果从某些顶点u到它的祖先v之间有一条回边,则该图有一个回路,这个回路是由DFS森林中从v到u的路径上的一系列树向边以及从u到v的回边构成的。
广度优先查找
- 可以从任何顶点开始访问图的顶点,每次迭代时,处理所有与当前顶点相邻的未访问顶点。
- 用队列来跟踪广度优先查找的操作较方便。
BFS的伪代码
bfs(v)
count := count + 1
标记 v= count
初始化顶点序列 v
while 序列非空 do
a := front of queue
for each vertex w adjacent to a do
if w is marked with 0
count := count + 1
mark w with count
add w to the end of the queue
remove a from the front of the queue
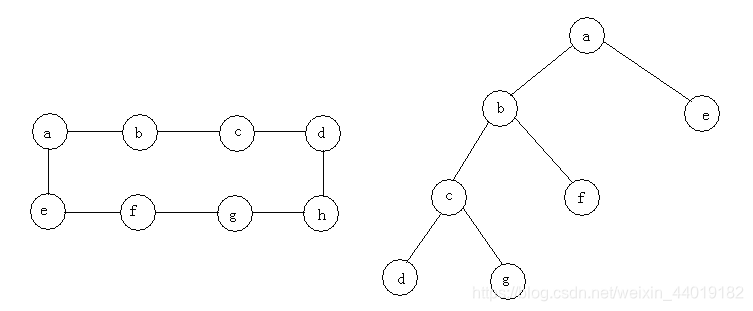
BFS举例
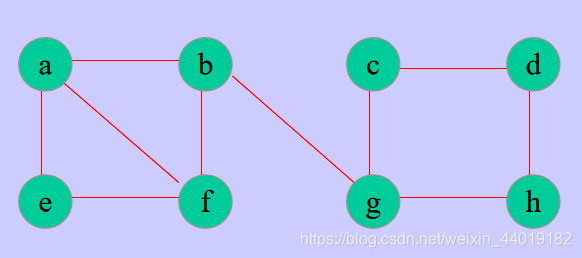
一个BFS的输出序列:
a-b-e-f-g-c-h-d
- 构造广度优先查找森林:遍历的初始顶点可以作为这样一个森林中第一颗树的根。无论何时,只要第一次遇到一个新的未访问顶点,它是从哪个顶点被访问到的,就把它附加为哪个顶点的子女。连接这样两个顶点的边称为树向边。如果一条边指向的是一个曾经访问过的顶点,并且这个顶点不是它的直接前趋(即它在树中的父母),这种边被称为交叉边。
- BFS也可以用来检查图的连通性和无环性。
- BFS可以用来求两个给定顶点间边的数量最少的路径:从两个给定的顶点中的一个开始BFS遍历,一旦访问到了另一个顶点就结束。从BFS树的根到第二个定间的最简单路径就是我们所求得的路径。
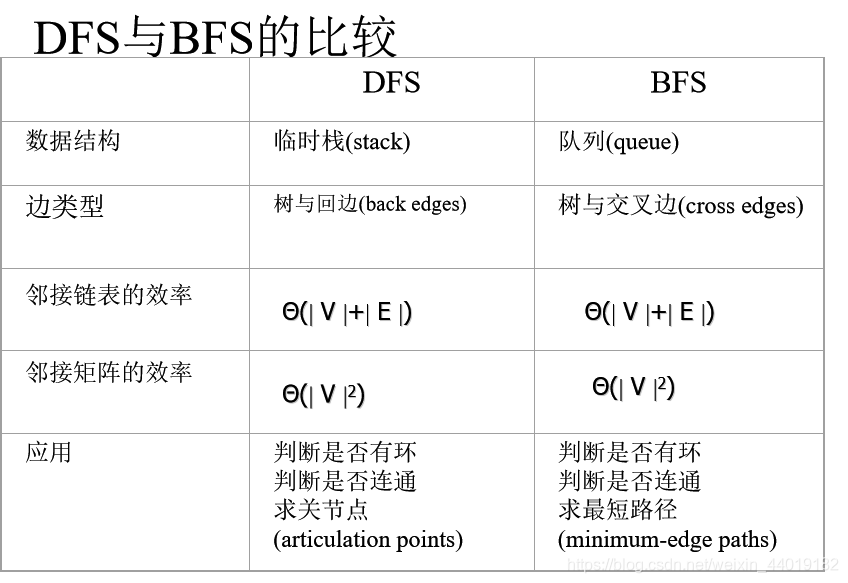
DFS与BFS的比较
拓扑排序
对给定的无环有向图,要求按照某种顺序列出它的顶点序列,使图的每一条边的起点总在结束顶点之前。
考虑五门必修课的一个集合{C1,C2,C3,C4,C5},一个在职的学生必须在某一阶段修完这几门课程。可以按照任何次序学习这些课程,只要满足下面这些先决条件:C1和C2没有任何先决条件,修完C1和C2才能修C3,修完C3才能修C4,而修完C3,C4才能修C5。这个学生每个学期只能修一门课程。这个学生应该按照什么顺序来学习这些课程?
求拓扑序列的方法1
方法1、应用DFS的出栈次序。
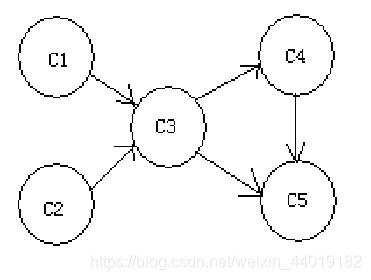
DFS序列:
C1-C3-C4-C5- -C2
出栈序列:
C5-C4-C3-C1-C2
拓扑排序:
C2-C1-C3-C4-C5
- 注意遍历到死端点时的出栈次序
- 拓扑排序不唯一
求拓扑序列的方法2
方法2、减治法,每次删除没有输入边的点。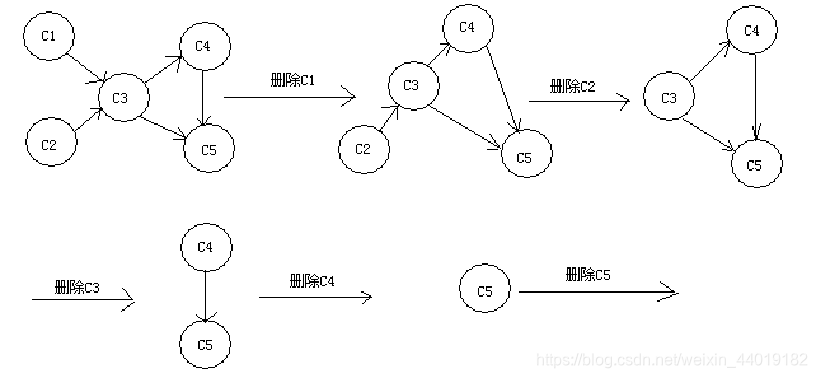
生成组合对象的算法
生成排列
排列问题指的是对于给定的多个元素求其中各种可能的序列。为了简单起见,这里仅仅考虑1到n之间的整数的排列问题
下面介绍三种生成方法:
- 插入法
- Johnson-Trotter 法
- 字典顺序法
插入法生列排列
举例:求n=3的排列
方法:在n=2的排列中插入3,
在n=1的排列中插入2。
过程:
在 1 中从右到左插入2得到 12,21
在 12 中从右到左插入3得到 123,132,312
在 21 中从右到左插入3得到 213,231,321
于是得 {123,132,312,213,231,321}
Johnson-Trotter 法生成排列
其实有的算法并不需要知道规模n-1的排列就可以直接得到规模n的排列结果,Johnson-Trotter算法就是其中一种。利用这一算法求得的排列序列还是相邻序列变化最小的一个序列集合,也就是说下一个序列与上一个序列仅仅交换了两个元素的位置 。
J-T方法举例
在排列的每一分量上画一个箭头。
求最大的移动整数k,不断移动元素,直到没有元素可移动为止,掉转所有大于k 的整数方向。
移动元素:如果分量k 的箭头指向一个相邻的较小元素,则该分量在排列中是移动的。
例n=3,从123开始:
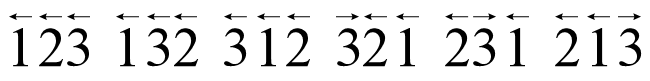
字典顺序生成排列
尽管Johnson-Trotter算法非常高效,但是似乎不是那么直观,不太符合人们的思维习惯。事实上比较自然的算法称为“字典排序(lexicographic order)算法”,它是根据单词在字典中的排列顺序得到的算法
字典生成顺序举例
例n=3
在{1,2,3}中按字典序选择:
123
132
213
231
312
321
生成子集
集合A的“幂集”是指以集合A的所有子集为元素组成的集合。
- 降低规模的减治法可以用来求幂集。
- 减治法的缺点也是在求解规模为n的问题时,需要得到规模为n-1的问题的解。这一过程是可以避免的,使用位串法求解集合幂集就是其中的一种解决方案。
减治法生成幂集
例n=3
方法:在n=2的幂集中加入元素3,在n=1的幂集中加入元素2
, {1} //n=1
, {1}, {2}, {1,2} //加入元素2
, {1}, {2}, {1,2}, {3}, {1,3}, {2,3}, {1,2,3}
//加入元素3
位串法生成幂集
例n=3,元素为{a1,a2,a3}
方法: 每一个子集与一个3位二进制串b1b2b3对应,ai属于该子集时,bi=1,否则 bi=0
二进制串:
000, 001, 010, 011, 100, 101, 110, 111
对应子集:
, {a3}, {a2}, {a2,a3}, {a1}, {a1,a3}, {a1,a2}, {a1,a2,a3}
减常因子法
假币问题
有n个金币,其中一个是假币。这个假币的重量比真币的重量要轻一点,所有n-1个金币的重量是一样的。现在你有一架天平,设计高效的算法(用最少的使用天平次数)找出那个假的金币。
用减治法(减半)
把n个硬币分为两堆,每堆n/2个,每次称一堆。
易见 W(1)=0
W(n)=W(n/2)+1
解得 W(n)= log2n
用减治法(减n/3)
把n个硬币分为三堆,每堆n/3个,每次称任意二堆。
易见 W(1)=0
W(n)=W(n/3)+1
解得 W(n)= log3n
结果比减半法更好。
约瑟夫斯问题
让n个人围成一个圈,并将他们从1到n编上号码。从编号为1的那个人那里开始这个残酷的计数,我们每次消去第二个人直到只留下一个幸存者。这个问题就是要求算出幸存者的号码J(n)。

- 把奇数n和偶数n的情况分开来考虑。
- 如果n为偶数,也就是说,n=2k,对整个圆圈处理第一遍后,生成了同样问题的规模减半的实例。容易发现,为了得到一个人的初始位置,只需要将它的新位置乘2并减去1。特别是对幸存者来说,这个关系会保持下去,也就是:J(2k)=2J(k)-1
- n(n>1)为奇数的情况,也就是n=2k+1。第一轮消去了所有偶数位置上的人。如果我们把紧接着消去的位置l上的人也加进来,我们留下了一个规模为k的实例。为了得到与新的位置编号相对应的初始位置编号,我们必须把新的位置编号乘2再加上1。因此,对于奇数n,我们有J(2k+1)=2J(k)+1
约瑟夫斯问题分析
- 一种求解方法是应用前向替换法.比方说求出J(n)的前15个值,找到一个模式,然后应用数学归纳法来证明它在一般情况下的合法性。
- 关于闭合式的最优雅的形式涉及到了规模n的二进制表示;我们可以对n本身做一次向左的循环移位来得到J(n)!例如,J(6)=J(1102)=1012=5,而J(7)=(1112)=1112=7。
减可变规模算法
计算中值和选择问题
选择问题:
求一个n数组的第k个最小元素。
当k=n/2时,该元素被称为中值。
方法:
利用快速排序的分区方法,将数组分成两部分,一部分大于值p,一部分小于值p,分割点s,若s=k则结束,若s<k,则在右边继续找第k-s小的元素。
计算中值举例
例如, 数组{4,1,10,9,7,12,8,2,15},求中值。
即求第k= [9/2]=5小的元素。
先数组{4,1,10,9,7,12,8,2,15}分区, 中轴=4
分区得:{1,2},{4},{ 9,7,12,8,10,15}, s1=3
因s1<k, 在{ 9,7,12,8,10,15} 中找k-s1=2
分区得:{7,8},{9},{12,10,15}, s2=3
因s2>k-s1, 在{7,8}中找s2+s1-k=1,
分区得:{8}
此时,s=k=5, 中值是8
插值查找
是查找有序数组的一种算法。设某次迭代处理的是数组最左边元素A[l]和最右边元素A[r]之间的部分,要查找的键值为v。写出过点(l,A[l])和点(r,A[r])的直线方程,取y=v,求出横坐标x,比较A[x]与v的值,决定是停止,还是在l与x-l之间或x+l与r之间继续查找
二叉查找树查找和插入
所谓的二叉查找树,它或者是一棵空树,或者满足以下的性质:
每个结点作为搜索对象,它的关键字是互不相同的。
对于树上的所有结点,如果它有左子树,那么左子树上所有结点的关键字都小于该结点的关键字。
对于树上的所有结点,如果它有右子树,那么右子树上所有结点的关键字都大于该结点的关键字。
对一般搜索表,也可以建立它相对应的二叉搜索树,并利用它作为数据结构进行搜索,这样的算法称为二叉搜索树搜索算法。它的优势是很明显的,它不但能够适应静态的搜索环境,也能够很好地运用到动态环境中。
但二叉查找树在最坏的情况下,n个元素的树的高度等于n,查找效率为Θ(n),平均效率则可达到Θ(logn).
二叉搜索树算法:
ALGORITHM BstSearch( R , k )
// 二叉搜索树上搜索算法的递归实现
// 输入:以R为根的二叉搜索树,待搜索值k
// 输出:搜索成功时,返回k在树中的位置,否则返回空值
if R = Null return Null
else if R.data > k
return BstSearch( R.leftChild , k )
else if R.data < k
return BstSearch( R.rightChild , k )
Else return R
ALGORITHM BstSearch2( R , k )
// 二叉搜索树上搜索算法的迭代实现
// 输入:以R为根的二叉搜索树,待搜索值k
// 输出:搜索成功时,返回k在树中的位置,否则返回空值
if R = Null return Null tmp ← R
while tmp ≠ Null do
if tmp.data = k return tmp
else if tmp.data > k tmp ← tmp.leftChild
else tmp ← tmp.rightChild