22-7-31

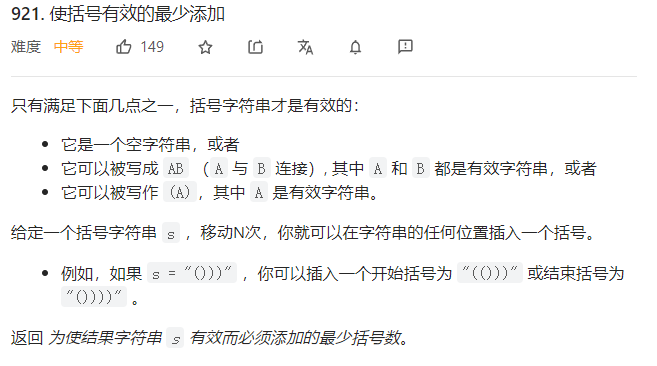
定义一个变量stack模拟栈，遇到左括号加1，遇到右括号减1，用来记录左右括号是否平衡，stack=0时即为平衡，遍历字符串，若在左右括号平衡（即stack=0）时遍历到右括号，说明该括号在之后一定无相匹配的括号，记录到变量remain中，依然认为左右括号平衡（即stack不变），最后stack与remain相加结果即为需要添加的括号数。

int minAddToMakeValid(char * s){
    int remain = 0, stack = 0;

    for(int i=0; s[i] != '\0'; ++i){    
        if(s[i] == '('){
            ++stack;
        }else{
            if(stack == 0)             
                ++remain;               
            else
                --stack;
        }
    }

    return remain + stack;

暴力破解

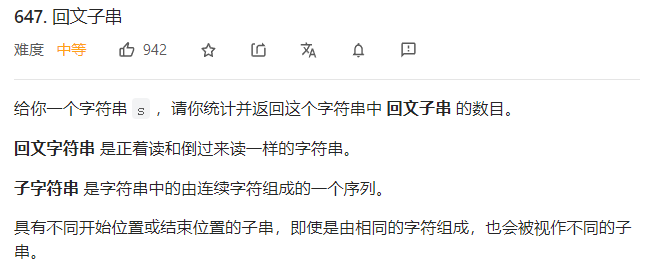
利用双指针和回文子串的基本性质，回文子串是正着读和倒过来读一样的字符串中的由连续字符组成的一个序列。
定义双指针遍历整个字符串，当s[i] == s[j]时，判断一下 i-j 是不是回文子串，是+1，不是+0

穷举子字符串

利用该方法判断每一个

int istrue(char * s,int left,int right){  
    while(left < right)
    {
        if(s[left] != s[right])
        {
            return 0;
        }
        left++;
        right--;
    }
    return 1;
}

int countSubstrings(char * s){
   int len=strlen(s);
   int sum=len;  
   for(int i=0;i<len;i++){
       for(int j=i+1;j<len;j++){
           if(s[i]==s[j]){
               sum=sum+istrue(s,i,j);
           }
       }
   }
   return sum;
}

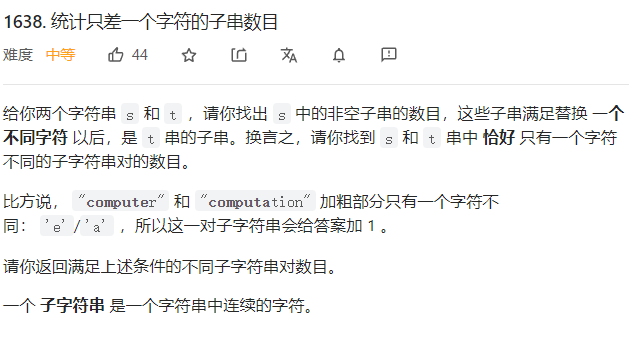
暴力破解

依次嵌套三循环穷举所有可能

int countSubstrings(char * s, char * t){
    if ((s == NULL) || (t == NULL) || (strlen(s) == 0) || (strlen(t) == 0)) {
        return 0;
    }
    int cnt = 0;
    for (int i = 0; i < strlen(s); i++) {
        for (int j = 0; j < strlen(t); j++) {
            int diff = 0;
            for (int k = 0; (i + k < strlen(s)) && ((j + k) < strlen(t)); k++) {
                if (s[i + k] != t[j + k]) {
                    diff++;
                }
                if (diff == 1) {
                    cnt++;
                }
                if (diff > 1) {
                    break;
                }
            }
        }
    }
    return cnt;
}

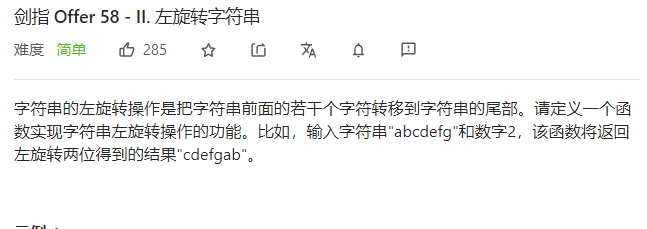
申请sizeof(char)*(strlen(s) + 1)的数组s1
先将s中[n,strlen(s))的字符存储到s1
然后再将s中[0,n）的字符存储到s1

在完成后得将’\0’存储到s1的最后一位
理由是返回的是字符串，需要有'\0'来作为结束位

char* reverseLeftWords(char* s, int n){
    char *s1 = (char *)malloc(sizeof(char)*(strlen(s) + 1));
    int j = 0;
    for (int i = n; i < strlen(s); i ++) {
        s1[j ++] = s[i];
    }
    for (int k = 0; k < n; k++ ) {
        s1[j ++] = s[k];
    }
    s1[j] = '\0';
    return s1;
}