放在前面的说明:
线性分组码是编码中的一个大类,设计线性分组码的说法不对的,这篇文章是我在刚开始复习专业课的时候写的,当时对这个没什么概念,只是从why and how to do 这个观念出发。但后来随着认识的加深,我才发现这篇文章实际上只说两件事 最小距离和纠错能力的关系 以及 汉明码的设计
由于时间关系其实我懒,就不重新整理了
如果是被标题骗进来的,扔另一个线性分组码的实现:RM码实现
首先我们先来复习一下线性分组码:
(n,k)线性分组码表示有k位的信息组,编码后为n位。根据生成矩阵的不同分为系统码和非系统码:系统码是码字中信息位与监督位分离,非系统码在码字中无法直观的得到原信息,在接收时需要额外译码。接收时由检校矩阵生成接收码字的伴随式S,并根据S判断该码字是否出错,依据S的形式对出错码字进行纠错。更加具体的内容参照:琪亚娜世界第一可爱
知道这些我们是可以应用线性分组码的,仍以前一篇博文中(7,3)码为例,我们可以在信源编码后接这一线性编码,从而提高通信的可靠性。但是上文所提及的(7,3)码只能对3bit信息组编码,如果我们是对10以内整数采用4bit的信源编码,显然就不能再用(7,3)码,此时需要我们去重新设计。那么现在问题就来了:我们怎么考察该种编码方式的检错纠错能力?编码后为几位?生成矩阵怎么设计?
首先说明如何去考察将检错纠错能力。
在这里引入几个名词
- 汉明重量
码组中所含1的数目,又称为码重,记为W c W_cWc - 汉明距离
两个码组中对应位置上具有不同二进制码元的个数,又称为码距,记为d ( c i , c j ) d(c_i,c_j)d(ci,cj)
接着说明 最小距离和纠错能力的关系
这里借用北邮课本中的解释:
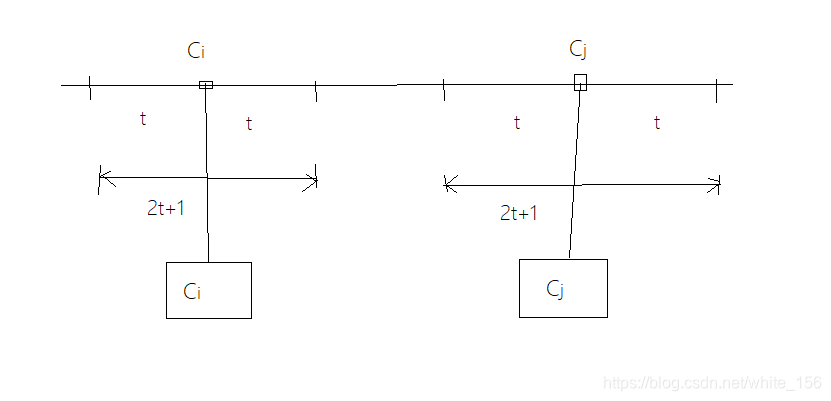
对于译码器来说,输入y共有2 n 2^n2n种合法输入,而输出c却只有2 k ( < 2 n ) 2^k(<2^n)2k(<2n)种输出,因此必然会有多个输入y对应一个输出c,这些输入就成为判决域.不妨假设判决域中,错误比特数不大于t时,也就是d ( y , c ) ≤ t d(y,c)\leq td(y,c)≤t,就可以纠正为正确的码字.若这一条对所有码字都成立,那么就意味着该编码可以纠正t个错误.此外,实现对每一个码字成立还需要保证码字判决域之间互不相交,即最小距离至少是2t+1
所以说码字的最小距离关系着线性分组码的纠错能力
上面的看不懂没有关系,因为以后是用不到的,虽然我也不知道这玩意有什么指导作用,谁设计矩阵的时候能把码距也算上,但是考试它考了啊
在线性分组码的译码过程中我们可以看到,对错误纠正实际上是根据伴随式形式确定错误,而且一种类型错误对应一个伴随式,不会出现多个错误对应一个伴随式的情况,从而区分在传输中到底是出现了何种错误。
仍以(7,3)码为例,以下是所有可能出现的伴随式
| 正确 | 0 0 0 0 |
|---|---|
| 错误 | 1 1 1 0 |
| 0 1 1 1 | |
| 1 1 0 1 | |
| 1 0 0 0 | |
| 0 1 0 0 | |
| 0 0 1 0 | |
| 0 0 0 1 |
所以由此可以得出纠错能力t与检校位数r的约束关系式
2 r ≥ C n 0 + C n 1 + C n 2 ⋯ C n t = ∑ i = 0 n C n i (1) 2^r \ge C_n^0 +C_n^1+C_n^2\cdots C_n^t=\sum_{i=0}^n C_n^i \tag{1}2r≥Cn0+Cn1+Cn2⋯Cnt=i=0∑nCni(1)
这个约束关系式表达的就是要为每一种错误分配一个伴随式。
关于这个关系式说明一点,为什么是从C n 0 C_n^0Cn0开始而不是C n 1 C_n^1Cn1
实际上,除了要给错误分匹位置,还要确定是否正确,这个C n 0 C_n^0Cn0表示的是全零伴随式,也就是正确码字对应的伴随式
特殊的,当上式取等时,又名汉明码可以纠正单个随机错误
此外,我们还可以从伴随式的角度出发去理解最小距离与纠错能力的关系
在前文说到伴随式S是检校矩阵H列向量1的线性组合,所以对于任意各有t个错误的两种错误e i e_iei和e j e_jej
S i ≠ S j ∑ k = 1 t e i k h i k ≠ ∑ k = 1 t e j k h j k ∑ k = 1 t e i k h i k + ∑ k = 1 t e j k h j k ≠ 0 \begin{aligned} S_i &\ne S_j \\ \sum_{k=1}^t e_{ik}h_{ik} &\ne \sum_{k=1}^t e_{jk}h_{jk} \\ \sum_{k=1}^t e_{ik}h_{ik}+\sum_{k=1}^t e_{jk}h_{jk} &\ne 0 \end{aligned}Sik=1∑teikhikk=1∑teikhik+k=1∑tejkhjk=Sj=k=1∑tejkhjk=0
也就是H中任意2 t 2t2t行都线性无关,而H中任意d-1行线性无关
d − 1 ≥ 2 t d-1 \ge 2td−1≥2t
所以有最小距离 d = 2 t + 1 d=2t+1d=2t+1
根据如上关系,也就能得知我们需要编码至少几位了n = r + k n=r+kn=r+k
其实上文所提的内容都只是对于设计起到一个指导作用,只能告诉我们具有存在性,而不具有实践性,下面给出几种线性分组码的设计
首先来看如何设计汉明码
关于汉明码的长度选择有如下公式(源于不等式(1) )
2 r − 1 = n 2^r-1=n2r−1=n
以r=3为例,计算编码后长度n=7,由此可得信息为k=4,故为(7,4)码。接下来为错误分配伴随式
| erorr sample | S |
|---|---|
| 100 0000 | 001 |
| 010 0000 | 010 |
| 001 0000 | 011 |
| 000 1000 | 100 |
| 000 0100 | 101 |
| 000 0010 | 110 |
| 000 0001 | 111 |
| 正确码字 | 000 |
|---|
根据上表可以得到接收码字( a 6 , a 5 , a 4 , a 3 , a 2 , a 1 , a 0 ) (a_6,a_5,a_4,a_3,a_2,a_1,a_0)(a6,a5,a4,a3,a2,a1,a0)和伴随式( S 2 , S 1 , S 0 ) (S_2,S_1,S_0)(S2,S1,S0)如下关系式
{ S 0 = a 6 + a 4 + a 2 + a 0 S 1 = a 5 + a 4 + a 1 + a 0 S 2 = a 3 + a 2 + a 1 + a 0 \begin{cases} S_0=a_6+a_4+a_2+a_0 \\ S_1=a_5+a_4+a_1+a_0 \\ S_2=a_3+a_2+a_1+a_0 \end{cases}⎩⎪⎨⎪⎧S0=a6+a4+a2+a0S1=a5+a4+a1+a0S2=a3+a2+a1+a0
对于正确的码字有S 2 = S 1 = S 0 = 0 S_2=S_1=S_0=0S2=S1=S0=0
{ a 6 + a 4 + a 2 + a 0 = 0 a 5 + a 4 + a 1 + a 0 = 0 a 3 + a 2 + a 1 + a 0 = 0 \begin{cases} a_6+a_4+a_2+a_0=0 \\ a_5+a_4+a_1+a_0=0 \\ a_3+a_2+a_1+a_0=0 \end{cases}⎩⎪⎨⎪⎧a6+a4+a2+a0=0a5+a4+a1+a0=0a3+a2+a1+a0=0
再根据如上关系写出检校矩阵H T H^THT
[ 1 0 0 0 1 0 1 1 0 0 0 1 1 0 1 0 1 1 1 1 1 ] \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix}⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡101010101100110001111⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
为了便于转换为生成矩阵,再将H T H^THT写为系统码的形式
[ 1 0 1 0 1 1 1 1 0 1 1 1 1 0 0 0 1 0 0 0 1 ] \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡101110001110101101001⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
进而通过检校矩阵获得生成矩阵G
[ 1 0 0 0 1 0 1 0 1 0 0 0 1 1 0 0 0 1 1 1 1 ] \begin{bmatrix} 1 & 0 & 0 & 0 & 1 & 0 & 1 \\ 0&1&0&0&0&1&1 \\ 0&0&0&1&1&1&1 \\ \end{bmatrix}⎣⎡100010000001101011111⎦⎤
此处说明 系统码生成矩阵与检校矩阵的关系
直接上结论 若有生成矩阵G = [ I ⋮ Q ] G=[ I \vdots Q]G=[I⋮Q],其对应生成矩阵H = [ Q T ⋮ I ] H=[Q^T \vdots I]H=[QT⋮I]
仿真代码见-> 德莉莎世界第一可爱
这里为什么是列向量而不是行向量呢?说行向量H T H^THT,转置之后就是列向量了 ↩︎