根据前序和中序确定一棵二叉树

#include <iostream>
#include <vector>
#include <queue>
#include <map>


using namespace std;


typedef struct node
{
	int val;
	struct node* left;
	struct node* right;
}node_t;

//创建一个存储中序遍历结果与下标的辅工具healper_map
map<int, int> healper_map;

void insert_node_to_tree(node_t* current_root, node_t* current_node)
{
	while (current_root != current_node)//循环体中，current_node找到正确位置后，让一步一步跟随它找位置的root指向它，从而退出位置查找
	{
		//在这里就需要判断current_node在root的左边还是右边，需要用到中序遍历的值与下标的映射关系map
		//如果待插的节点的下标小于根节点的下标，待插的节点在根的左边
		if (healper_map[current_node->val] < healper_map[current_root->val])
		{
			if (current_root->left == NULL)
			{
				current_root->left = current_node;
			}

			current_root = current_root->left;
		}
		else
		{
			if (current_root->right == NULL)
			{
				current_root->right = current_node;
			}

			current_root = current_root->right;
		}
	}
}

//通过前序遍历和中序遍历确定一棵二叉树
//思路分析
//1.通过前序遍历的第一个元素或者后续遍历的最后一个元素，可以确定整棵树的根
//2.依次遍历前序或者后序的元素，可以遍历到二叉树的每一个节点，在遍历每一个节点的时候可以通过中序遍历确定当前遍历的节点应该插在直系根的左边还是右边
//总之就是利用了前序或者后序结果确定二叉树的根，通过中序遍历可以确定待插节点应该插在根的左边还是右边
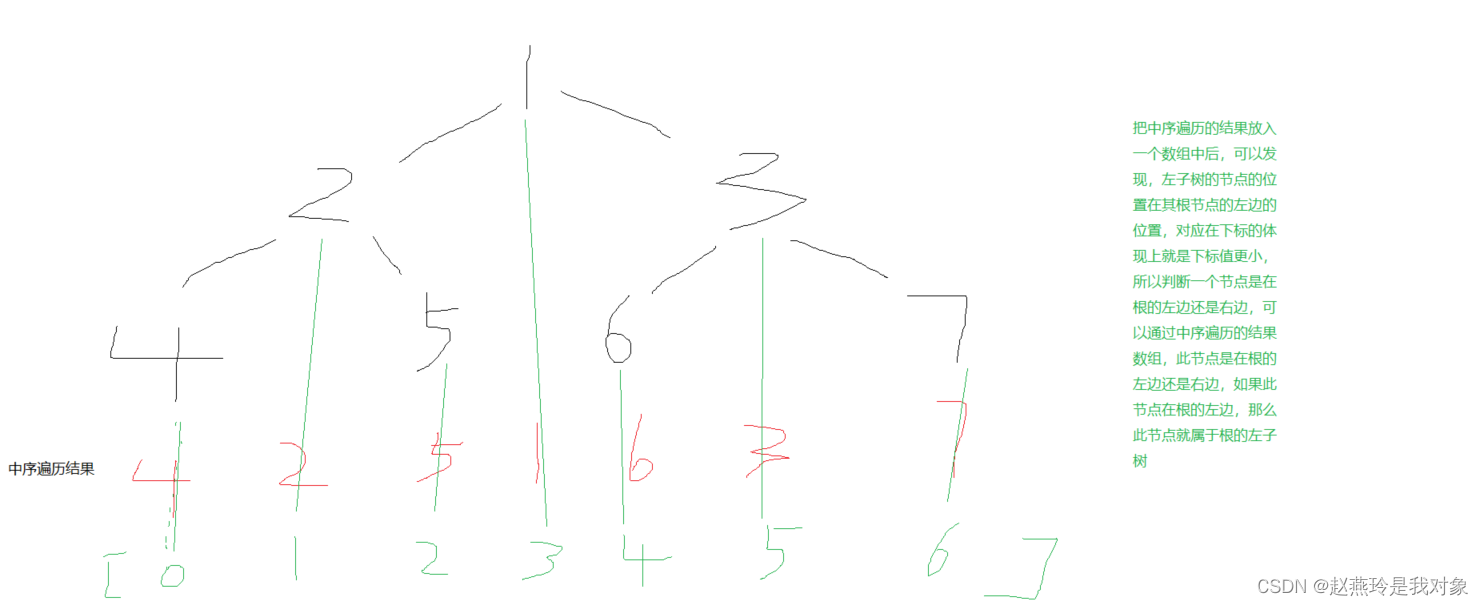
//中序遍历的特点通过结合二叉树的图和中序遍历的结果，可以发现，如果把中序遍历的结果按顺序放入一个数组中，叶子节点的下标值小于根节点
//反过来说，当你确定一个根以后，如果当前遍历的叶子节点对应的下标小于根节点对应的下标，那么这个叶子节点在根的左边
node_t* get_tree(vector<int> pre_order_vec, vector<int> middle_order_vec)
{
	if (pre_order_vec.size() <= 0) return nullptr;

	//确定整棵树的根
	node_t* root = new node_t;
	root->val = pre_order_vec[0];
	root->left = NULL;
	root->right = NULL;

	//通过for循环，遍历完中序遍历序列中的所有元素
	for (int i = 0; i < middle_order_vec.size(); i++)
	{
		//以中序序列中的元素值middle_order_vec[i]作为key
		//以位置i作为value
		//存放到哈希表中
		//比如中序遍历序列中的元素是[A, D, E, F, G, H, M, Z]
		//那么这个哈希表就是以下的样子
		//| 索引 | 位置
		//   A       0
		//   D       1
		//   E       2
		//   F       3 
		//   G       4
		//   H       5
		//   M       6
		//   Z       7
		healper_map[middle_order_vec[i]] = i;
	}

	//依次遍历前序vec的除了第一个节点以外的所有节点
	for (int i = 1; i < pre_order_vec.size(); i++)
	{
		node_t* current_node = new node_t;
		current_node->val = pre_order_vec[i];
		current_node->left = NULL;
		current_node->right = NULL;

		//把当前遍历的节点插入正在创建的这棵树上
		insert_node_to_tree(root, current_node);
	}

	return root;
}

int main()
{
	vector<int> pre_order_vec = {1, 2, 4, 5, 3, 6, 7};
	vector<int> middle_order_vec = {4, 2, 5, 1, 6, 3, 7};
	node_t* root = get_tree(pre_order_vec, middle_order_vec);
}