记录洛谷刷题C语言QAQ
「PMOI-0」潇湘の雨
题目背景
(原 LZOI-1,改名已经 PMOI 成员同意)
lhm-01
题目描述
言琢დ 在一个 2 n × 2 n 2n \times 2n2n×2n 的矩阵中坐标为 ( x , y ) (x,y)(x,y) 的一个点上。
现在 Lanuxhem 需要任意选择矩阵上的一个点作为起点,然后依次经过 k kk 个点,移动规则如下:
每次移动只能选择与目前相邻(上下左右)的点作为本次移动的目标点。不能选择矩阵外的点。
每一轮移动必须正好经过矩阵上的所有点,不能重复经过同一个点。每经过所有点后,视为一轮移动结束。
注意依次经过 k kk 个点后,最后一轮移动可能并没有完成。
现在 Lanuxhem 想知道,他最少会经过 言琢დ 多少次。
输入格式
第一行输入四个正整数 n , k , x , y n,k,x,yn,k,x,y。
输出格式
第一行输出一个整数,表示答案。
样例 #1
样例输入 #1
2 16 1 1
样例输出 #1
1
提示
样例说明
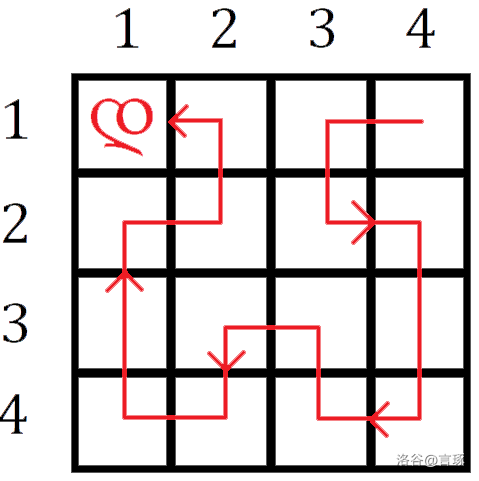
დ \color{red}დდ 代表 言琢დ 所在位置,红色线表示 Lanuxhem 第一轮的路径。
数据规模与约定
本题采用捆绑测试。
| 子任务编号 | 分值 | n , k ≤ n,k\len,k≤ |
|---|---|---|
| 1 11 | 30 3030 | 1 0 4 10^4104 |
| 2 22 | 30 3030 | 1 0 9 10^9109 |
| 3 33 | 40 4040 | 1 0 18 10^{18}1018 |
对于所有数据,保证 1 ≤ n , k ≤ 1 0 18 1\le n,k\le10^{18}1≤n,k≤1018,1 ≤ x , y ≤ 2 n 1\le x,y\le 2n1≤x,y≤2n。
代码如下:
#include<string.h>
#include<stdio.h>
#include<math.h>
#include <stdlib.h>
long long n,k,x,y;
int main()
{
scanf("%lld%lld%lld%lld",&n,&k,&x,&y);
printf("%lld\n",k/4/n/n);
return 0;
}
[CSP-J 2021] 分糖果
题目背景
红太阳幼儿园的小朋友们开始分糖果啦!
题目描述
红太阳幼儿园有 n nn 个小朋友,你是其中之一。保证 n ≥ 2 n \ge 2n≥2。
有一天你在幼儿园的后花园里发现无穷多颗糖果,你打算拿一些糖果回去分给幼儿园的小朋友们。
由于你只是个平平无奇的幼儿园小朋友,所以你的体力有限,至多只能拿 R RR 块糖回去。
但是拿的太少不够分的,所以你至少要拿 L LL 块糖回去。保证 n ≤ L ≤ R n \le L \le Rn≤L≤R。
也就是说,如果你拿了 k kk 块糖,那么你需要保证 L ≤ k ≤ R L \le k \le RL≤k≤R。
如果你拿了 k kk 块糖,你将把这 k kk 块糖放到篮子里,并要求大家按照如下方案分糖果:只要篮子里有不少于 n nn 块糖果,幼儿园的所有 n nn 个小朋友(包括你自己)都从篮子中拿走恰好一块糖,直到篮子里的糖数量少于 n nn 块。此时篮子里剩余的糖果均归你所有——这些糖果是作为你搬糖果的奖励。
作为幼儿园高质量小朋友,你希望让作为你搬糖果的奖励的糖果数量(而不是你最后获得的总糖果数量!)尽可能多;因此你需要写一个程序,依次输入 n , L , R n, L, Rn,L,R,并输出你最多能获得多少作为你搬糖果的奖励的糖果数量。
输入格式
输入一行,包含三个正整数 n , L , R n, L, Rn,L,R,分别表示小朋友的个数、糖果数量的下界和上界。
输出格式
输出一行一个整数,表示你最多能获得的作为你搬糖果的奖励的糖果数量。
样例 #1
样例输入 #1
7 16 23
样例输出 #1
6
样例 #2
样例输入 #2
10 14 18
样例输出 #2
8
样例 #3
样例输入 #3
见附件中的 candy/candy3.in。
样例输出 #3
见附件中的 candy/candy3.ans。
提示
【样例解释 #1】
拿 k = 20 k = 20k=20 块糖放入篮子里。
篮子里现在糖果数 20 ≥ n = 7 20 \ge n = 720≥n=7,因此所有小朋友获得一块糖;
篮子里现在糖果数变成 13 ≥ n = 7 13 \ge n = 713≥n=7,因此所有小朋友获得一块糖;
篮子里现在糖果数变成 6 < n = 7 6 < n = 76<n=7,因此这 6 66 块糖是作为你搬糖果的奖励。
容易发现,你获得的作为你搬糖果的奖励的糖果数量不可能超过 6 66 块(不然,篮子里的糖果数量最后仍然不少于 n nn,需要继续每个小朋友拿一块),因此答案是 6 66。
【样例解释 #2】
容易发现,当你拿的糖数量 k kk 满足 14 = L ≤ k ≤ R = 18 14 = L \le k \le R = 1814=L≤k≤R=18 时,所有小朋友获得一块糖后,剩下的 k − 10 k - 10k−10 块糖总是作为你搬糖果的奖励的糖果数量,因此拿 k = 18 k = 18k=18 块是最优解,答案是 8 88。
【数据范围】
| 测试点 | n ≤ n \len≤ | R ≤ R \leR≤ | R − L ≤ R - L \leR−L≤ |
|---|---|---|---|
| 1 11 | 2 22 | 5 55 | 5 55 |
| 2 22 | 5 55 | 10 1010 | 10 1010 |
| 3 33 | 10 3 {10}^3103 | 10 3 {10}^3103 | 10 3 {10}^3103 |
| 4 44 | 10 5 {10}^5105 | 10 5 {10}^5105 | 10 5 {10}^5105 |
| 5 55 | 10 3 {10}^3103 | 10 9 {10}^9109 | 0 00 |
| 6 66 | 10 3 {10}^3103 | 10 9 {10}^9109 | 10 3 {10}^3103 |
| 7 77 | 10 5 {10}^5105 | 10 9 {10}^9109 | 10 5 {10}^5105 |
| 8 88 | 10 9 {10}^9109 | 10 9 {10}^9109 | 10 9 {10}^9109 |
| 9 99 | 10 9 {10}^9109 | 10 9 {10}^9109 | 10 9 {10}^9109 |
| 10 1010 | 10 9 {10}^9109 | 10 9 {10}^9109 | 10 9 {10}^9109 |
对于所有数据,保证 2 ≤ n ≤ L ≤ R ≤ 10 9 2 \le n \le L \le R \le {10}^92≤n≤L≤R≤109。
【感谢 hack 数据提供】
wangbinfeng
代码如下:
#include<string.h>
#include<stdio.h>
#include<math.h>
#include <stdlib.h>
int n,l,r;
int main(){
scanf("%d%d%d",&n,&l,&r);
if(l/n==r/n)
printf("%d\n",r%n);
else
printf("%d\n",n - 1);
return 0;
}
[Kubic] Addition
题目背景
建议先看 B 题题目背景。
题目描述
有一个初始长度为 n nn 的序列 a aa。你需要进行 n − 1 n-1n−1 次操作。每一次操作先在当前序列中选出两个相邻的数 x , y x,yx,y 并删除(原序列中 x xx 在 y yy 左边),再往原位置插入一个 x + y x+yx+y 或一个 x − y x-yx−y。n − 1 n-1n−1 次操作之后最终只会剩下恰好一个数,求这个剩下的数的最大值。
输入格式
第一行,一个整数 n nn。
第二行,共 n nn 个整数 i ii 个表示 a i a_iai。
输出格式
共一行,一个整数,表示答案。
样例 #1
样例输入 #1
5
-1 1 1 -1 1
样例输出 #1
3
提示
对于 100 % 100\%100% 的数据,1 ≤ n ≤ 1 0 5 , ∣ a i ∣ ≤ 1 0 9 1\le n\le 10^5,|a_i|\le 10^91≤n≤105,∣ai∣≤109。
| 分值 | n nn | ∣ a i ∣ \vert a_i\vert∣ai∣ | 特殊性质 | |
|---|---|---|---|---|
| Subtask 1 \operatorname{Subtask}1Subtask1 | 10 1010 | ≤ 2 \le 2≤2 | 无特殊限制 | 无 |
| Subtask 2 \operatorname{Subtask}2Subtask2 | 20 2020 | ≤ 100 \le 100≤100 | 无特殊限制 | 无 |
| Subtask 3 \operatorname{Subtask}3Subtask3 | 5 55 | 无特殊限制 | 无特殊限制 | a i ≥ 0 a_i\ge 0ai≥0 |
| Subtask 4 \operatorname{Subtask}4Subtask4 | 30 3030 | 无特殊限制 | ≤ 1 \le 1≤1 | 无 |
| Subtask 5 \operatorname{Subtask}5Subtask5 | 35 3535 | 无特殊限制 | 无特殊限制 | 无 |
样例解释
一种操作过程如下:
-1 1 1 -1 1
-1 1 1 -2
-1 1 3
-1 4
3
可以证明没有更优的方案。
代码如下:
#include<string.h>
#include<stdio.h>
#include<math.h>
#include <stdlib.h>
int n,x;
long long f[2];
int main()
{
scanf("%d%lld",&n,&f[1]);
for(int i=2;i<=n;i++,x^=1)
{
scanf("%lld",&f[x]);
f[x]=f[x]<0?f[x^1]-f[x]:f[x^1]+f[x];
}
printf("%lld\n",f[x^1]);
return 0;
}
[COCI2021-2022#1] Ljeto
题目描述
有两支四人队伍,菠萝和蓝莓,在玩水枪。
我们将会给定游戏的具体信息,共 n nn 条,信息形如在 t i t_iti 秒,玩家 a i a_iai 打到了玩家 b i b_ibi,对于一个玩家 i ii,如果 1 ≤ i ≤ 4 1\le i\le 41≤i≤4,那么他在菠萝队,否则他在蓝莓队,每打到一下加 100 100100 分。
定义一次双喷为,在 10 1010 秒之内,一名队员连续打到对面队伍的队员,设这名队员第一次命中是在第 t f t_ftf 秒,则第二次命中需要在第 [ t f + 1 , t f + 10 ] [t_f+1,t_f+10][tf+1,tf+10] 秒内,一次双喷可以为队伍增加 50 5050 分,可以连续触发双喷。
试求出两支队伍的得分。
输入格式
第一行为一个整数 n nn。
接下来 n nn 行,一行三个整数 t i , a i , b i t_i,a_i,b_iti,ai,bi。
保证所有 t i t_iti 互不相同,并且按升序输入。
输出格式
输出一行两个整数,分别表示两支队伍的得分。
样例 #1
样例输入 #1
3
10 1 6
20 1 7
21 8 1
样例输出 #1
250 100
样例 #2
样例输入 #2
3
10 2 5
15 2 6
25 2 5
样例输出 #2
400 0
样例 #3
样例输入 #3
2
10 5 2
11 6 3
样例输出 #3
0 200
提示
数据范围
对于全部数据,1 ≤ n ≤ 100 1\le n\le 1001≤n≤100,0 ≤ t i ≤ 1 0 3 0\le t_i\le 10^30≤ti≤103,∀ 1 ≤ i < n , t i < t i + 1 \forall 1\le i< n,t_i<t_{i+1}∀1≤i<n,ti<ti+1,1 ≤ a i , b i ≤ 8 1\le a_i,b_i\le 81≤ai,bi≤8,玩家 a i a_iai 与玩家 b i b_ibi 不属于同一支队伍。
| Subtask | 特殊限制 | 分值 |
|---|---|---|
| 1 11 | n ≤ 3 n\le 3n≤3 | 10 1010 |
| 2 22 | 不存在双喷 | 15 1515 |
| 3 33 | 无特殊限制 | 25 2525 |
说明
本题总分 50 5050 分。
本题译自 Croatian Open Competition in Informatics 2021/2022 Contest #1 T1 Ljeto。
代码如下:
#include<string.h>
#include<stdio.h>
#include<math.h>
#include <stdlib.h>
int n,m,p,q,x,y,time;
int t[9];//上次打中人的时间
int main()
{
for(int i=1;i<=8;i++) t[i]=-99;//先定义没打中过人
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d%d%d",&time,&p,&q);
if(p<=4)//如果菠萝队的人打中的
{
if(time-t[p]>=1&&time-t[p]<=10)//判断双喷
{
x+=50;
}
t[p]=time;
x+=100;
}
if(p>4)//如果草莓队的人打中的
{
if(time-t[p]>=1&&time-t[p]<=10)//判断双喷
{
y+=50;
}
t[p]=time;
y+=100;
}
}
printf("%d %d",x,y);
}
[COCI2007-2008#5] TRI
题目描述
Mirko 在他的数学笔记本上写下了一个包含三个正整数 a , b , c a,b,ca,b,c、一个等号和一个四则运算符(加号、减号、乘号、除号)的等式。但是在另一节课上,Mirko 的朋友 Slavko 将等式中的等号和运算符从他的笔记本上擦除了。
请您通过这三个整数还原这个等式以帮助 Mirko。
输入格式
一行,三个整数 a , b , c a,b,ca,b,c。
输出格式
一行,一个包含以上三个整数 a , b , c a,b,ca,b,c(顺序与输入相同),一个等号和一个四则运算符的字符串,表示一种可能的算式。
如果有多个可能解,输出其中任意一个即可。
样例 #1
样例输入 #1
5 3 8
样例输出 #1
5+3=8
样例 #2
样例输入 #2
5 15 3
样例输出 #2
5=15/3
提示
对于 100 % 100\%100% 的数据,0 < a , b , c < 100 0< a,b,c< 1000<a,b,c<100。
输入数据保证有解,但不保证有唯一解。
本题分值按照原比赛设置,满分 20 2020 分。
代码如下:
#include<string.h>
#include<stdio.h>
#include<math.h>
#include <stdlib.h>
int a,b,c;
int main(){
scanf("%d%d%d",&a,&b,&c);
if(a+b==c)//八种情况
printf("%d+%d=%d",a,b,c);
else if(a-b==c)
printf("%d-%d=%d",a,b,c);
else if(a*b==c)
printf("%d*%d=%d",a,b,c);
else if(a/b==c)
printf("%d/%d=%d",a,b,c);
else if(b+c==a)
printf("%d=%d+%d",a,b,c);
else if(b-c==a)
printf("%d=%d-%d",a,b,c);
else if(b*c==a)
printf("%d=%d*%d",a,b,c);
else if(b/c==a)
printf("%d=%d/%d",a,b,c);
return 0;
}