【Java高级数据结构】二叉树的遍历及相关操作

二叉树的遍历

所谓树的遍历，就是按某种次序访问树中的结点，要求每个结点访问一次且仅访问一次。

根据二叉树的结点结构，二叉树的基本结构是由根结点、左子树和右子树三个基本单元组成的，因此只要依次遍历这三部分，就遍历了整个二叉树。

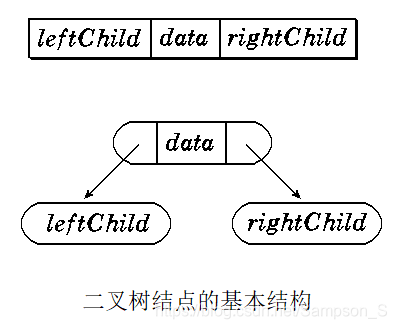
如果用 L、D、R 分别表示遍历左子树、访问根结点、遍历右子树，那么对二叉树的遍历顺序就可以有六种方式：

• 1、访问根结点、遍历左子树、遍历右子树，记作 DLR。
• 2、访问根结点、遍历右子树、遍历左子树，记作 DRL。
• 3、遍历左子树、访问根结点、遍历右子树，记作 LDR。
• 4、遍历右子树、访问根结点、遍历左子树，记作 RDL。
• 5、遍历左子树、遍历右子树、访问根结点，记作 LRD。
• 6、遍历右子树、遍历左子树、访问根结点，记作 RLD。

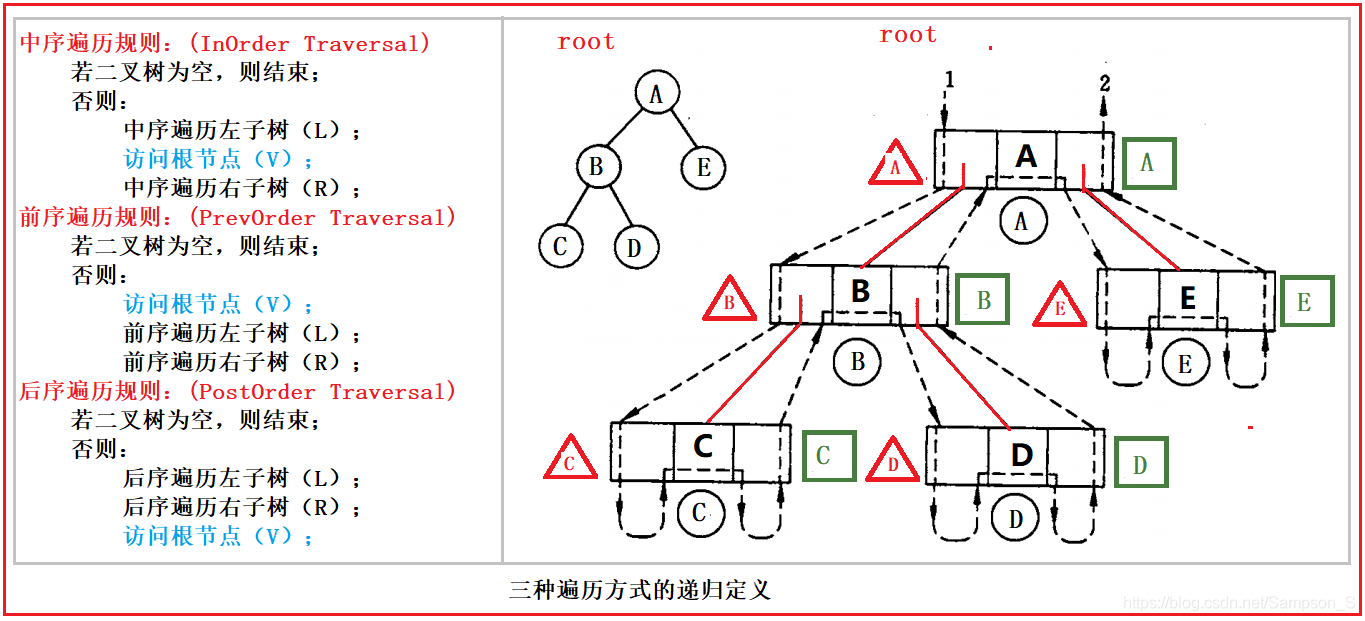
在以上六种遍历方式中，如果规定按先左后右的顺序，那么就只剩下 DLR、LDR和LRD 三种。根据对根结点的访问的先后顺序不同，分别称 DLR 为先序遍历或先根遍历，LDR 为中序遍历（对称遍历），LRD 为后序遍历。

下面就分别介绍三种遍历方式的递归定义。

下面，我们来看一个例子，如图所示的二叉树，其先序、中序、后序遍历的序列如下。

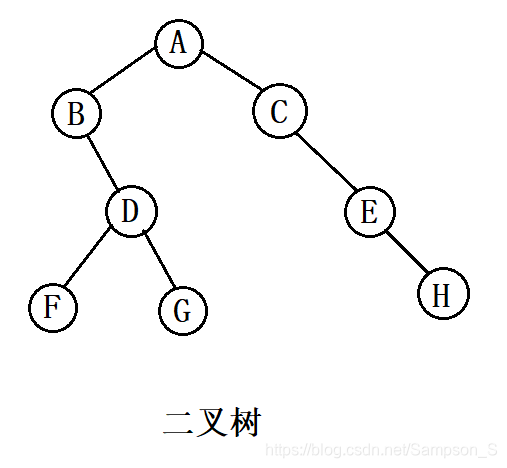
• 先序遍历：A、B、D、F、G、C、E、H。
• 中序遍历：B、F、D、G、A、C、E、H。
• 后序遍历：F、G、D、B、H、E、C、A。

最早提出遍历问题的是对存储在计算机中的表达式求值。例如，(a+b*c)-d/e。该表达式用二叉树表示如图所示.

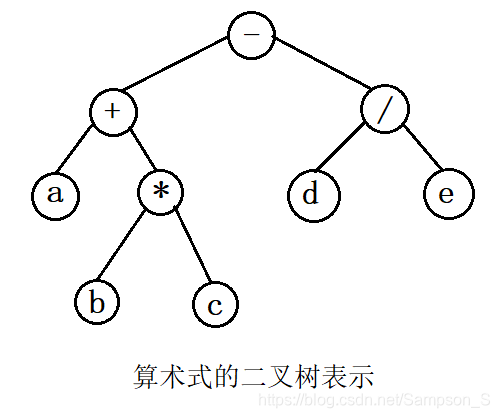
当对此二叉树进行先序、中序、后序遍历时，便可以获得表达式的前缀、中缀、后缀书写形式，如下所示。

• 前缀：- + a * b c / d e
• 中缀：a + b * c - d / e
• 后缀：a b c * + d e / -

其中，中缀形式是算术表达式的通常形式，只是没有括号。前缀表达式称为波兰表达式。算术表达式的后缀表达式称为逆波兰表达式。在计算机内，使用后缀表达式易于求值。其具体操作如四则运算的实现。

下面以二叉链表作为存储结构来具体讨论二叉树的遍历算法。

使用递归算法实现二叉树的遍历：

• 中序遍历

/**
 * 递归实现中序遍历
 * @param btNode
 */
private void InOrder(BtNode<T> btNode){
    if(btNode != null){
        InOrder(btNode.leftChild);
        System.out.print(btNode.data+" ");
        InOrder(btNode.rightChild);
    }
}
public void InOrder(){
    InOrder(root);
    System.out.println();
}

• 先序遍历

/**
 * 递归实现前序遍历
 * @param btNode
 */
private void PrevOrder(BtNode<T> btNode){
    if(btNode != null){
        System.out.print(btNode.data+" ");
        PrevOrder(btNode.leftChild);
        PrevOrder(btNode.rightChild);
    }
}
public void PrevOrder(){
    PrevOrder(root);
    System.out.println();
}

• 后序遍历

/**
 * 递归实现后序遍历
 * @param btNode
 */
private void LastOrder(BtNode<T> btNode){
    if(btNode != null){
        LastOrder(btNode.leftChild);
        LastOrder(btNode.rightChild);
        System.out.print(btNode.data+" ");
    }
}
public void LastOrder(){
    LastOrder(root);
    System.out.println();
}

使用非递归算法实现二叉树的遍历：

• 中序遍历

/**
 * 非递归实现中序遍历
 */
public void NiceInOrder(){
    if(root == null){
        return;
    }
    BtNode<T> btNode = root;
    Stack<BtNode> stack = new Stack<>();
    while (!stack.empty() || btNode != null) {
        while (btNode != null) {
            stack.push(btNode);
            btNode = btNode.leftChild;
        }
        System.out.print(stack.peek().data + " ");
        btNode = stack.pop();
        btNode = btNode.rightChild;
    }
    System.out.println();
}

• 先序遍历

/**
 * 非递归实现前序遍历
 */
public void NicePrevOrder(){
    if(root == null){
        return;
    }
    Stack<BtNode> stack = new Stack<>();
    stack.push(root);
    while (!stack.empty()){
        BtNode<T> btNode = stack.pop();
        System.out.print(btNode.data+" ");
        if(btNode.rightChild != null){
            stack.push(btNode.rightChild);
        }
        if(btNode.leftChild != null){
            stack.push(btNode.leftChild);
        }
    }
    System.out.println();
}

• 后序遍历

/**
 * 非递归实现后序遍历
 */
public void NiceLastOrder(){
    if(root == null){
        return;
    }
    BtNode<T> tag = null; //标记指针，判断结点的左子树和右子树是否都遍历过
    BtNode<T> btNode = root;
    Stack<BtNode> stack = new Stack<>();
    while (!stack.empty() || btNode != null) {
        while (btNode != null) {
            stack.push(btNode);
            btNode = btNode.leftChild;
        }
        btNode = stack.pop();
        if(btNode.rightChild == null || btNode.rightChild == tag) {
            System.out.print(btNode.data + " ");
            tag = btNode;
            btNode = null;
        }else {
            stack.push(btNode);
            btNode = btNode.rightChild;
        }
    }
    System.out.println();
}

• 层次遍历

/**
 * 非递归实现层次遍历
 */
public void NiceLevelOrder(){
    if(root == null) return;
    Queue<BtNode> queue = new LinkedList<BtNode>();
    queue.add(root);
    while (!queue.isEmpty()){
        BtNode<T> btNode = queue.peek();
        System.out.print(btNode.data+" ");
        queue.remove();
        if(btNode.leftChild != null){
            queue.add(btNode.leftChild);
        }
        if(btNode.rightChild != null){
            queue.add(btNode.rightChild);
        }
    }
    System.out.println();
}

二叉树的其他相关操作

二叉树的创建：

/**
 * 二叉树的创建
 * @return
 */
private BtNode CreateTreeA(){
    BtNode<T> btNode = null;
    Character item = new java.util.Scanner(System.in).next().charAt(0);
    if(item != '#'){
        btNode = new BtNode<>((T)item);
        btNode.leftChild = CreateTreeA();
        btNode.rightChild = CreateTreeA();
    }
    return btNode;
}
public void CreateTree(){
    root = CreateTreeA();
    System.out.println();
}

求二叉树结点的个数：

/**
 * 求二叉树结点的个数
 * @param node
 * @return
 */
private int GetSize(BtNode node){
    if(node == null){
        return 0;
    }else {
        return GetSize(node.leftChild) + GetSize(node.rightChild) + 1;
    }
}
public int GetSize(){
    return GetSize(root);
}

求二叉树的深度：

private int GetDepth(BtNode node){
    if(node == null){
        return 0;
    }else {
        return Math.max(GetDepth(node.leftChild),GetDepth(node.rightChild)) + 1;
    }
}
public int GetDepth(){
    return GetDepth(root);
}

判断是否是BST树：

public boolean Is_BST_Tree() {
    boolean tag = true;
    if (root == null) return tag;
    BtNode ptr = root;
    BtNode pre = null;
    Stack<BtNode> stack = new Stack<>();
    while (ptr != null || !stack.empty()) {
        while (ptr != null) {
            stack.push(ptr);
            ptr = ptr.leftChild;
        }
        ptr = stack.pop();
        if (pre != null) {
            if (ptr.data < pre.data) {
                tag = false;
                break;
            }
        }
        pre = ptr;
        ptr = ptr.rightChild;
    }
    return tag;
}