目录
矩阵的迹
一个n×n矩阵A的主对角线(从左上方至右下方的对角线)上各个元素的总和被称为矩阵A的迹(或迹数)
边缘分布

协方差
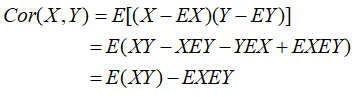
协方差例题
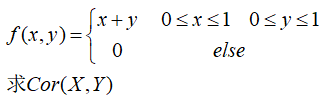
解

协方差性质

从协方差到相关系数
我们可以通过皮尔逊相关系数将两组变量之间的关联度规整到一定的取值范围内(-1,1)。皮尔逊相关系数如下:
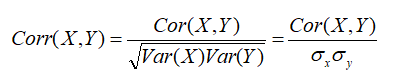
#Cov而非Cor
皮尔逊相关系数的性质


主成分分析
算法动机
- 在降维过程中,要尽可能将数据向方差大的方向投影,去除原始数据之间的冗余性,使得数据所蕴含的信息没有丢失,彰显个性。
- 一旦发现方差最大的投影方向,则继续寻找保持方差第二的方向且进行投影。

算法描述

降维后n个l维样本数据Y的方差为:

降维前n个d维样本数据X的协方差矩阵为:
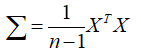
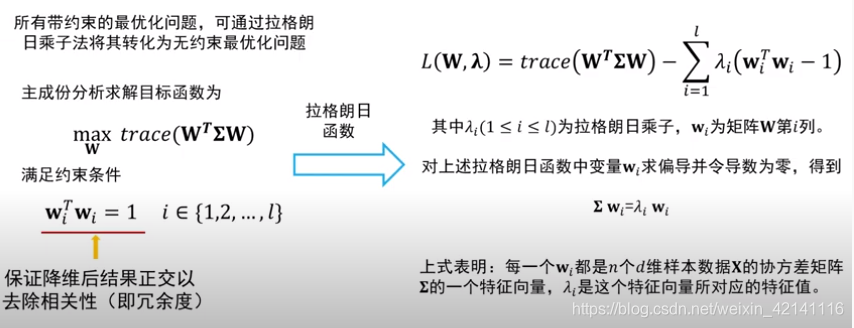
组成份分析的求解目标函数为:

满足约束条件:(为了所得到的映射结果的相关性最小)
![]()
算法描述


版权声明:本文为weixin_42141116原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。