HGSM——基于层级结构图的相似度分析

HGSM算法(Hierarchical-graph-based Similarity Measurement)，基于层级结构图的相似度分析：主要是基于用户的历史位置信息挖掘用户之间的相似度。与其他关于位置信息的算法不同的地方在于它考虑了人们运动行为的序列性质和地理空间的层次性。

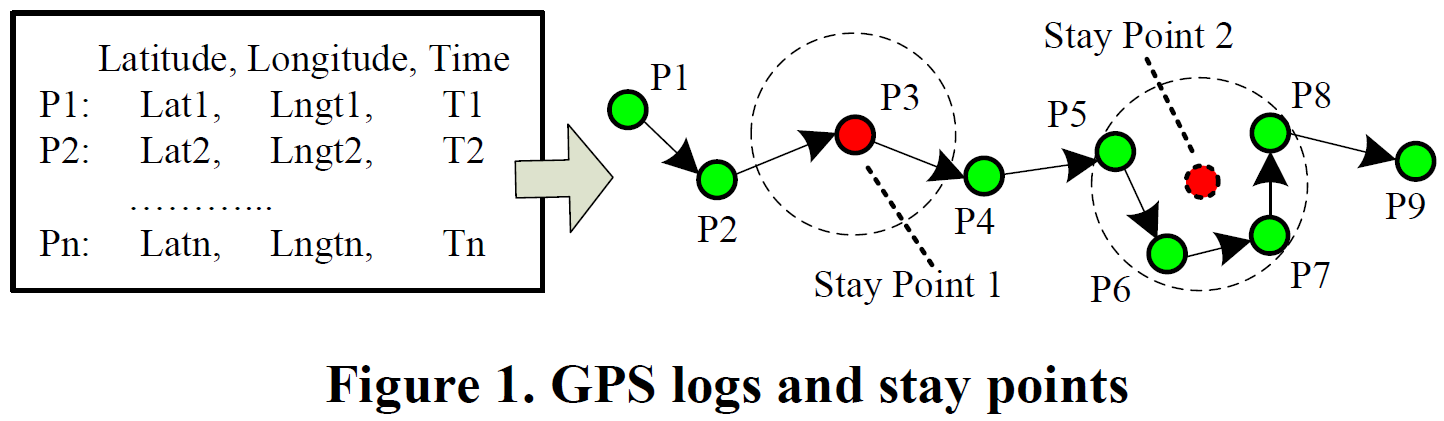
GPS记录：一系列GPS数据点的有序集合， $P=\{p_1, p_2, \ldots , p_n\}$ 。每个GPS数据点 $p_i=(Lat_i, Lngt_i, T_i)$ 。图一左边是一个GPS记录，将这些点描绘在一个二维平面内，得到一个GPS轨迹，如右图。
这里写图片描述

根据GPS记录提取停留点
1、GPS记录是由很多个GPS数据点组成的，其中有很多不带有什么意义；
2、每一个GPS数据点都或多或少地存在着误差；
3、当用户进入室内场所时，可能得不到当时的GPS数据，直到重新到达室外。

图一右图中有两种类型的停留点:
停留点1：在某一段时间内，用户的位置信息是静止不动的，可能用户进了一个没有信号的房子里。
停留点2：在某一段时间内，用户一直在一个特定的区域内徘徊，产生了很多GPS数据点，因此我们需要把这些数据点取平均位置作为一个停留点。

定义：如果在一定范围（D<200m）内，用户停留超过一定时间（T>30min），则认为用户在这一地点进行了停留，取这一部分GPS点的平均值作为停留点坐标，取第一个GPS点的时间戳作为到达时间（arvT），取最后一个GPS点的作为离开时间（levT），记作：

S P = (P^, a r v T, l e v T)

$SP=(\hat{P}, arvT, levT)$
范围D、时间T的选取可以根据不同情况进行调整，选择合适的数值就可以避免一些无意义的停留点的出现，比如交通堵塞。

下面是检测停留点的算法：
这里写图片描述

根据GPS轨迹和检测出的停留点，用户的历史位置记录可以表示成一系列带有到达时间和离开时间的地点。由于不同的用户的停留点很多都是不同的，很难对其进行比较，用停留点之间的距离来度量用户相似度也会误差很大。

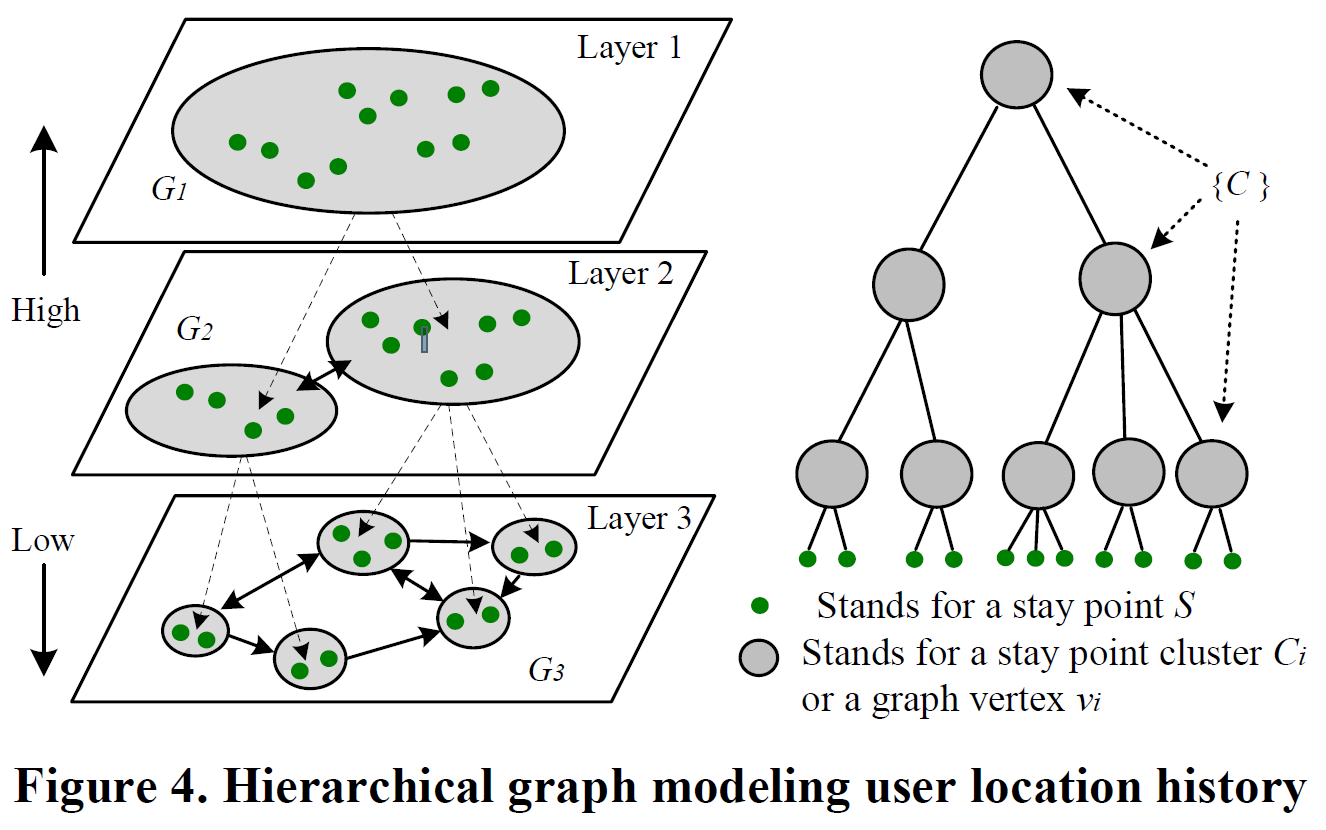
为了解决这个问题提出了层级结构图。将所有用户的停留点放在一个数据集内，再对这个数据集进行层次聚类，得到几个不相交的空间区域。所以不同用户相似的停留点在每一层中将会被分在同一个区域内。
这里写图片描述
随着层级降低，空间区域的个数变多，每个空间区域的规模变小，在更低层级上有相同历史位置记录的用户比高层级上相同历史位置记录的用户更相似。

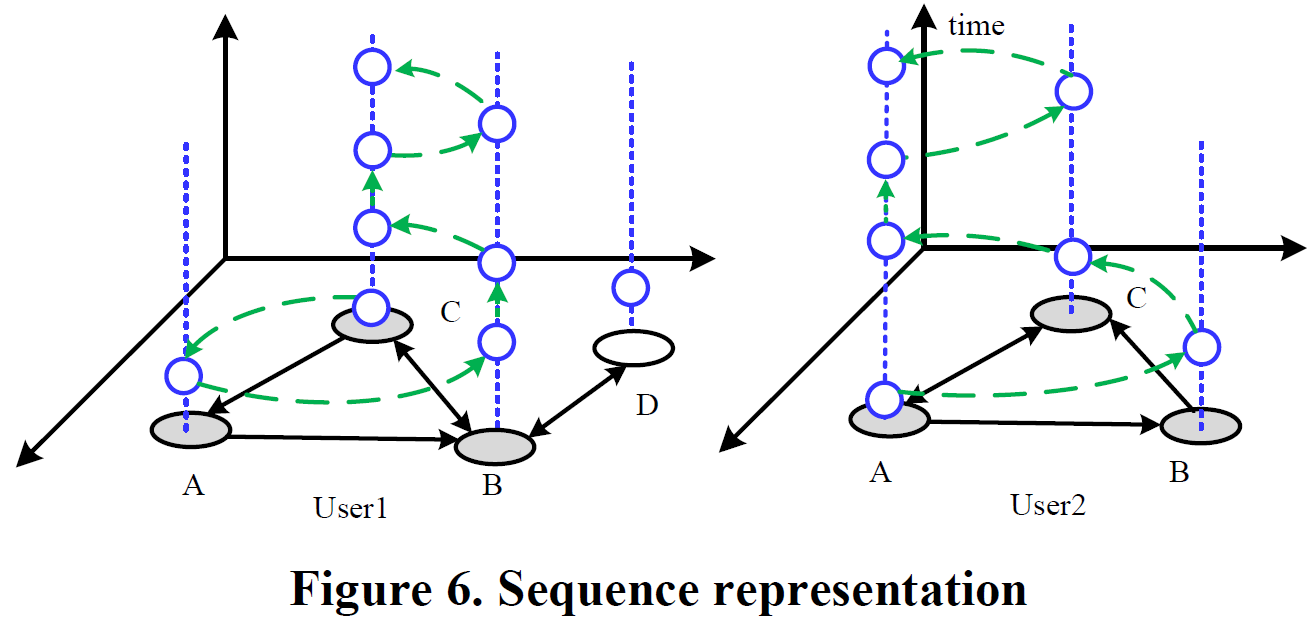
聚类之后我们用层级结构图来表示用户的历史位置信息，比如：
这里写图片描述
首先找到两个用户共有的区域，这里是A,B和C区域，用户1的位置序列为 <C,A,B,B,C,C,B,C><script type="math/tex" id="MathJax-Element-114"> </script>，用户2的位置序列为 <A,B,C,A,A,C,A><script type="math/tex" id="MathJax-Element-115"> </script>，更进一步，我们把位置序列表示为：

U s e r 1 : C (1) - \to - Δ t 1 A (1) - \to - Δ t 2 B (2) - \to - Δ t 3 C (2) - \to - Δ t 4 B (1) - \to - Δ t 5 C (1) U s e r 1 : A (1) - \to - Δ t' 1 B (1) - \to - Δ t' 2 C (1) - \to - Δ t' 3 A (2) - \to - Δ t' 4 C (1) - \to - Δ t' 5 A (1)

$User 1 : C(1)\xrightarrow[]{\Delta t_1}A(1)\xrightarrow[]{\Delta t_2}B(2)\xrightarrow[]{\Delta t_3}C(2)\xrightarrow[]{\Delta t_4}B(1)\xrightarrow[]{\Delta t_5}C(1)\\ User 1 : A(1)\xrightarrow[]{\Delta t_1'}B(1)\xrightarrow[]{\Delta t_2'}C(1)\xrightarrow[]{\Delta t_3'}A(2)\xrightarrow[]{\Delta t_4'}C(1)\xrightarrow[]{\Delta t_5'}A(1)$

Δti $\Delta t_i$ 表示两个地点之间的时间间隔。

因此我们可以用地理区域序列来表示用户的历史位置记录：

s e q = < a 1 (k 1) - \to - Δ t 1 a 2 (k 2) - \to - Δ t 2 \dots - \to - - Δ t i - 1 a i (k i) - \to - Δ t i a i + 1 (k i + 1) - \to - - Δ t i + 1 \dots > Δ t i = a i + 1 (0) . a r v T - a i (k i - 1) . l e v T

$seq=<a_1(k_1)\xrightarrow[]{\Delta t_1}a_2(k_2)\xrightarrow[]{\Delta t_2}\ldots\xrightarrow[]{\Delta t_{i-1}}a_i(k_i)\xrightarrow[]{\Delta t_i}a_{i+1}(k_{i+1})\xrightarrow[]{\Delta t_{i+1}}\ldots>\\ \Delta t_i=a_{i+1}(0).arvT-a_i(k_i-1).levT$

序列匹配：
相似序列：两个序列是相似的，当且仅当他们满足下面的条件：

s e q 1 = < a 1 (k 1) - \to - Δ t 1 a 2 (k 2) - \to - Δ t 2 \dots a m (k m) > s e q 2 = < b 1 (k' 1) - \to - Δ t' 1 b 2 (k' 2) - \to - Δ t' 2 \dots b m (k' m) >

$seq1=<a_1(k_1)\xrightarrow[]{\Delta t_1}a_2(k_2)\xrightarrow[]{\Delta t_2}\ldots a_m(k_m)>\\ seq2=<b_1(k_1')\xrightarrow[]{\Delta t_1'}b_2(k_2')\xrightarrow[]{\Delta t_2'}\ldots b_m(k_m')>$
1、

∀1≤i≤m,ai=bi,i.e. $\forall 1\leq i \leq m, a_i=b_i, i.e.$
2、

∀1≤i≤m,|Δti−Δt′i|≤tth $\forall 1\leq i \leq m, |\Delta t_i-\Delta t_i'|\leq t_{th}$ ，

tth $t_{th}$ 是一个预先定义的时间阈，成为时态约束。

如果上面两个条件都成立，则序列 $seq_1$ 和 $seq_2$ 所包含的相似序列sseq为：

< b 1 (m i n (k 1, k' 1)) \to b 2 (m i n (k 2, k' 2)) \to \dots b m (m i n (k m, k' m)) >

如果相似序列的有m个节点，则称为m-length similar sequence。如果一个相似序列不被其他任何相似序列包含，则称为最长相似序列(maximum-length similar sequence)。

最长相似序列查找算法：
这里写图片描述
算法中有两个操作，序列延伸和剪枝，这两个操作交替反复进行，直到序列的所有节点都被扫描。延伸是把一个长度为m的相似序列延伸为长度为(m+1)的相似序列，这个操作从长度为1的相似序列开始。剪枝是把除了最长相似序列以外的序列都去掉。

相似序列越长，这个过程会越耗时。但是相似序列越长，它出现的概率就越低，因此，为了提高序列匹配的效率，设置一个参数maxLength，当相似序列长度达到maxLength时停止迭代。

相似性度量：
现在用检索得到的相似序列来计算两个序列的总体相似性得分。先对每一层级所有的最长相似序列得分加和，再对所有层级的得分加和。这里需要考虑两个因素：相似序列的长度和相似序列所在的层级。

一个m-length相似序列的相似性得分为：

S (m) = α (m) \sum i = 1 m m i n (k i, k' i)

$S_{(m)}=\alpha_{(m)}\sum_{i=1}^mmin(k_i,k_i')$

两个用户在某个层级上的相似性得分是这个层级上所有最长相似序列的得分之和：

S l = 1 N 1 \times N 2 \sum i = 1 n s i

$S_l=\frac{1}{N_1\times N_2}\sum_{i=1}^ns_i$
其中

N1 $N_1$ 和

N2 $N_2$ 分别为两个用户的停留点数目。除以停留点数目是为了防止用户的数据不平衡，如果不考虑数据的规模，拥有很多停留点的用户与其他用户的相似度得分将比较少停留点的用户多。

最后再对每个层级的相似度得分加权求和：

S o v e r a l = \sum l = 1 H β l S l

$S_{overal}=\sum_{l=1}^H\beta_lS_l$
层级越低，权重越高。

最后用MAP(Mean Average Precision平均准确率)和nDCG(Normalized discounted cumulative gain归一化折损累积增益)来衡量算法的质量。

HGSM算法的优势：
序列性质：能够区分像<A→B→C><script type="math/tex" id="MathJax-Element-131"> </script>和 <B→A→C><script type="math/tex" id="MathJax-Element-132"> </script>的序列。
层级性质：一方面，相比于高层级，在低层级上更能准确地判断用户间的相似度。高层级可能没有办法区分同在一个城市活动的人。
但另一方面，如果只考虑低层级上的相似性，就可能会忽略用户在高层级上的活动，那一些相似用户就会被判定为不相似，比如两个人都经常往返于北京和西雅图，但在北京内或西雅图内他们的活动轨迹并不相似。

原文链接：https://blog.csdn.net/BaiJingting/article/details/51519913