最小二乘法拟合圆弧

步骤：（1）分离出目标（如下二值图像中的白色区域）；
（2）提取目标边缘坐标；
（3）查找所要拟合的边缘坐标；
（4）最小二乘法拟合圆弧。
本文要拟合的边缘如实验图中绿色区域，根据检测出的坐标特点提取出所要拟合的边缘坐标。
实验图和结果图如下所示：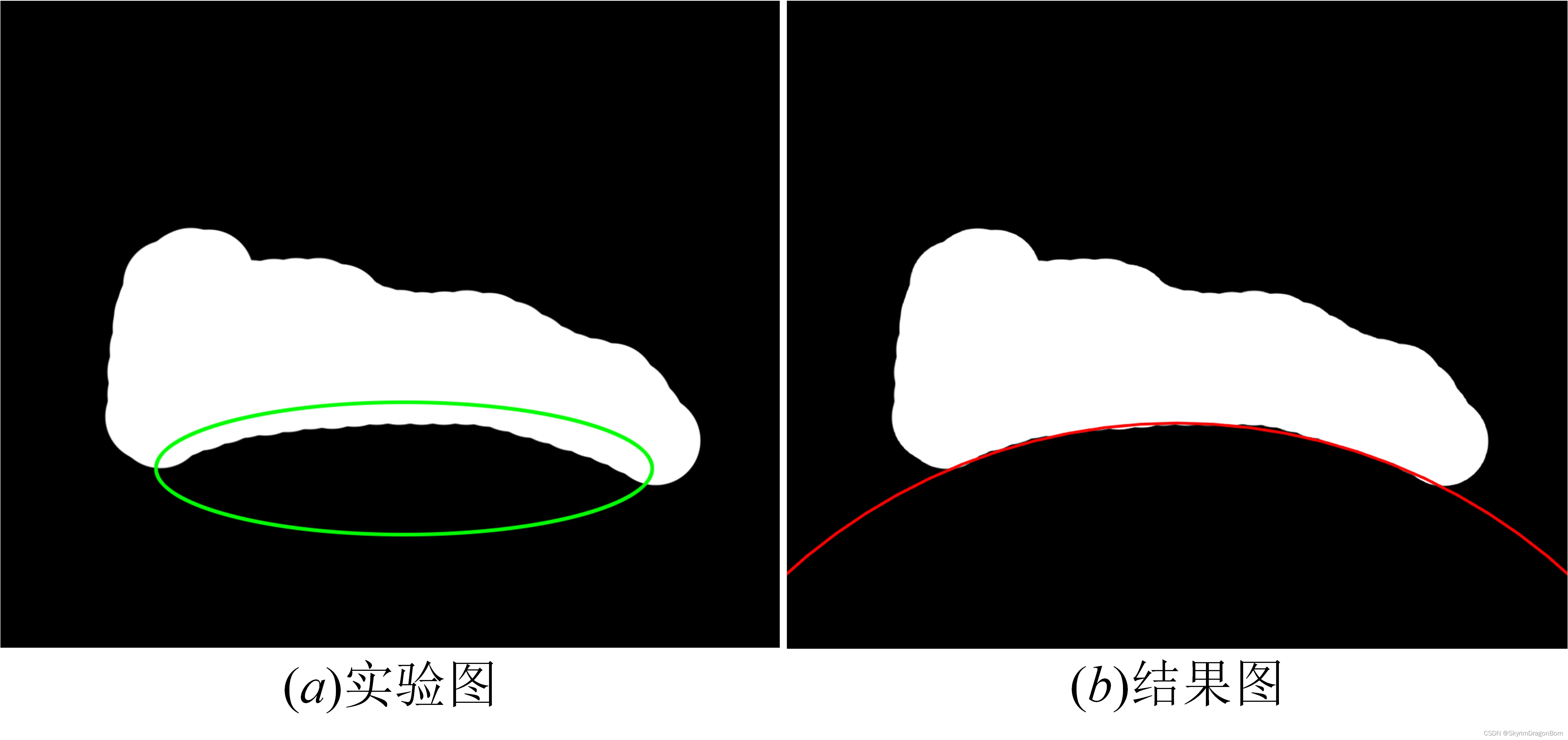

MATLAB实现：

clear; close all; clc;
Origin=im2gray(imread('circle.png'));
BW=edge(Origin,'canny');
[y,x] = find(BW>0);
Coordinate=[x y];
j=0;
delta=100;  %控制坐标范围
%提取所要拟合的边缘坐标
for i=Coordinate(1,1)+delta:Coordinate(end,1)-delta
    index=find(Coordinate(:,1)==i, 1, 'last' );
    j=j+1;
    X(j)=Coordinate(index,1);
    Y(j)=Coordinate(index,2);
end
 
X = X';	%所有边缘点的X坐标
Y = Y';	%所有边缘点的Y坐标

%最小二乘法圆拟合
N = size(X,1);    
C = (N*sum(X.^2)-sum(X).^2);
D = (N*sum(X.*Y)-sum(X)*sum(Y));
E = N*sum(X.^3)+N*sum(X.*Y.^2)-sum(X.^2+Y.^2)*sum(X);
G = (N*sum(Y.^2)-sum(Y)*sum(Y));
H = N*sum(X.^2.*Y)+N*sum(Y.^3)-sum(X.^2+Y.^2)*sum(Y);

a = (H*D-E*G)/(C*G-D.^2);
b = (H*C-E*D)/(D.^2-G*C);
c = -(sum(X.^2+Y.^2)+a*sum(X)+b*sum(Y))/N;

x0 = -a/2;	%圆心X坐标
y0 = -b/2;	%圆心Y坐标
R = sqrt(a.^2+b.^2-4*c)/2;	%半径

figure;imshow(Origin);
alpha=0:pi/50:2*pi; %角度[0,2*pi]
hold on;
x=x0+R*cos(alpha);
y=y0+R*sin(alpha);
plot(x,y,'-r','LineWidth',2);