返回一个二维整数数组中的最大子数组的和

一.课题要求：
          输入一个二维整形数组，数组里有正数也有负数；
          二维数组中连续的一个子矩阵组成一个子数组，没个子数组都有一个和；
         如果数组A[0]……A[j-1]首尾相邻，允许A[i-1]，…… A[n-1]，A[0]……A[j-1]之和最大。 同时返回最大子数组的位置
二.设计思路：
        从总左边（a[0]）开始遍历整个数组，一直到最右边结束（a[n-1]），在这个过程中记录到目前为止最大的子数组和maxsofar。假如我们已经找到a [0] 到 a[n-1]之间的最大子数组和，要么“还是a[0]到a[i-1]之间的最大子数组和”，要么是“从a[i]开始，往前几个连续的数的最大值”。 在求从a[i]开始，往前几个连续的数的最大值时，从a[i]开始往前几个连续的数的最大值maxending_i等于(maxending_i-1)+a[i]和0两者之中的最大值，即maxending_i=max((manending_i-1)+a[i],0)
三. 程序代码
#include<iostream>
using namespace std;
int max(int a,int b)
{
    if(a>b)
    {return a;
    }
    else 
    {return b;
    }
}
int maxsum(int a,int n)
{
    int i;
    int maxsofar=0;//maxsofar记录到目前为止的最大值
    int maxendinghere=0;//maxendinghere记录从当前位置开始网前几个连续的数的和的最大值
    for(i=0;i<n;i++)
    {
        maxendinghere=max(maxendinghere+a[i],0);
        maxsofar=max(maxsofar,maxendinghere);
    }
    return maxsofar;
}
int main()
{
    int n,a i=0;
    cout<<"请输入数组：";
        cin>>a[i];
    int max=maxsum(a,n);
    cout<<最大子数组的和为："<<max<<endl;
        return 0;
}

四.结果截图

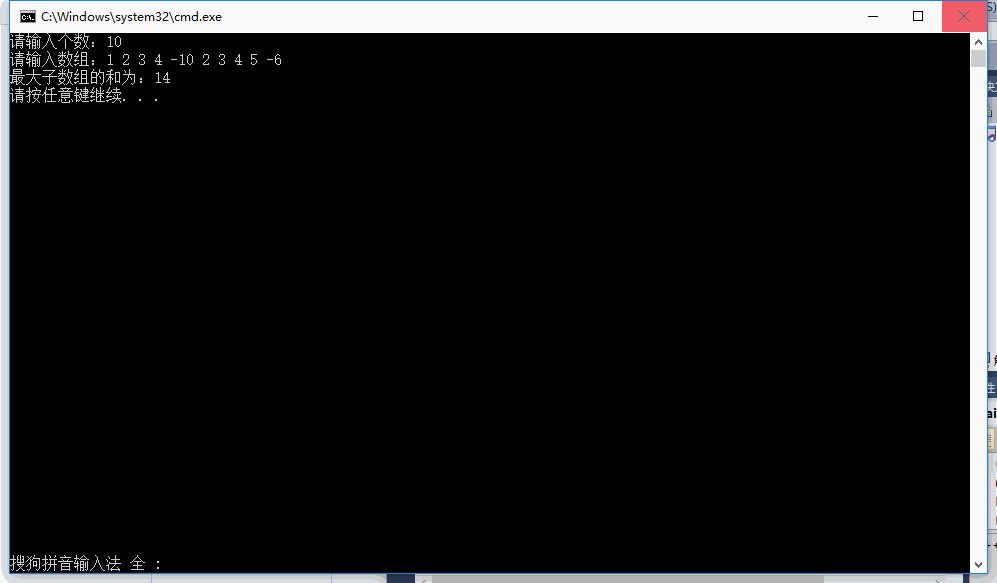
五.时间记录日志

六.收获总结
     通过这次作业，我理解了如何使数组A[0]……A[j-1]首尾相邻，允许A[i-1]，…… A[n-1]，A[0]……A[j-1]之和最大。 同时返回最大子数组的位置

七.小组成员

    滕达

 

转载于:https://www.cnblogs.com/tengda123/p/9904922.html