资源中有关于计算机图形学的基本图形的扫描转换的介绍详细PPT讲解以及一个小提纲的介绍帮助你的掌握，再附上颜色渐变直线，椭圆、圆中点Bresenham算法，双光源线框球Gouraud光照模型算法等基本操作的exe图形演示，可以自己动手看看效果的，欢迎下载~~
下载地址：https://download.csdn.net/download/weixin_53919192/86799612

一. 前言

二. 直线的扫描转换

2.1 Bresenham算法的特点：

一. 前言

直线、圆、椭圆是二维场景中的最基本图形。尽管MFC的CDC类已经提供了相关的绘制函数，但直接使用这些函数仍然无法满足真实感图形绘制的要求。光栅扫描显示器是画点设备，基本图形的光栅化就是在像素点阵中确定最佳逼近于理想图形的像素点集，并用指定颜色显示这些像素点集的过程。当光栅化与按扫描线顺序绘制图形的过程结合在一起时，也称为扫描转换。本章从基本图形的生成原理出发，使用绘制像素点函数实现基本图形的扫描转换。绘制像素点函数的原型为 BOOL SetPixelV(int x, int y, COLORREF crColor);
直线、圆、椭圆的扫描转换主要使用中点算法实现。

二. 直线的扫描转换

直线的扫描转换是在屏幕像素点阵中确定最佳逼近于理想直线的像素点集的过程。计算机图形学要求直线的绘制速度要快，即尽量使用加减法（增量算法），避免乘、除、开方、三角等复杂运算。最著名的算法是由J.E. Bresenham于1965年提出的Bresenham算法，这里介绍的是中点画线算法。

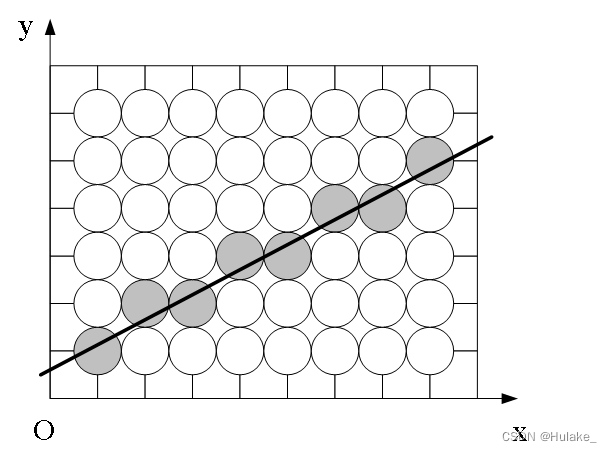
光栅扫描显示器的本质决定它难以生成完美的直线段，也不能保证直线段精确地通过起点和终点。
绘制直线段的基本要求：
直线要直。要求具有精确的起点和终点。
直线无方向性。从起点绘制到终点的直线段与从终点绘制到起点的直线段要重合。
直线的绘制速度要快。即尽量使用加减法整数运算，避免乘、除、开方、三角等复杂运算。

2.1 Bresenham算法的特点：

Bresenham算法是一个经典的增量算法。在一个迭代算法中，如果每一步的x，y值是用前一步的值加上一个增量来获得的，那么这种算法就称为增量算法。
Bresenham算法有几种变体，计算方法略有不同。本章只介绍中点Bresenham算法（Midpoint Bresenham Algorithm）。
对于直线，中点Bresenham算法与Bresenham算法产生同样的像素点，而且还可以扩展为更复杂的图形扫描转换算法，如绘制圆的中点Bresenham算法和绘制椭圆的中点Bresenham算法。

2.2 算法原理

中点画线算法的原理：每次在主位移方向上走一步，另一个方向上走不走步取决于中点误差项的值。
给定理想直线的起点坐标为P0(x0,y0)，终点坐标为P1(x1,y1),则直线的隐函数方程为：

理想直线将平面划分成三个区域：对于直线上的点，F(x，y)＝0；对于直线上方的点，F（x，y）＞0；对于直线下方的点，F（x，y）＜0。
假设直线的斜率为0≤k≤1，则|△x|≥|△y|，x0<x1,y0<y1 。所以确定x方向为主位移方向。x方向上每次加1，y方向上加不加1取决于中点误差项的值。

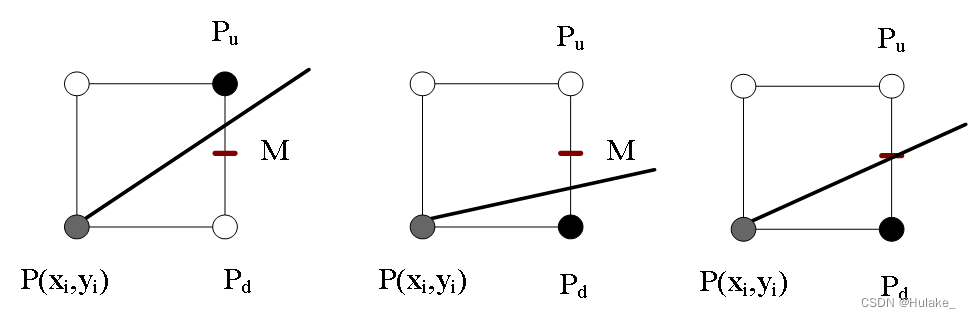
假定直线的当前点是P，沿主位移x方向走一步，下一点只能在Pu 和Pd两点中选取，Pu和Pd的中点为M 。显然，若中点M在理想直线的下方，则Pu点距离直线近，否则选取Pd。

2.3 构造中点误差项

从Pi(xi,yi）点出发选取下一像素时，需将Pu和Pd的中点M(x i＋1,y i＋0.5)代入隐函数方程，构造中点误差项di 。

2.4 具体算法

一）：

int x=x0,y=y0;
int dx=abs(x0-x1),dy=abs(y0-y1);
int temp,interchange,f,i;
int s1,s2;
if (x1>x0) s1=1; else s1=-1;//sign(x1-x0)
if (y1>y0) s2=1; else s2=-1; //sign(y1-y0)
if (dy>dx)
{
    temp=dx;
    dx=dy;
    dy=temp;
    interchange=1;
}
else interchange=0;

二）：

f=dx-2*dy;
for (i=1;i<=dx;i++)
{
    setpixel(x,y,color);
    if (interchange==1) 
        y=y+s2; 
    else 
        x=x+s1;//x++;
    if (f<0)
    {
        if (interchange==1) 
            x=x+s1;
        else 
            y=y+s2;//y++
        f=f-2*dx;
    }
    f=f+2*dy;
}//for

2.5 直线的中点算法小结

确定主位移方向。在主位移方向上每次加1，另一个方向上加不加1，取决于中点误差项。
计算f的初始值。
区分f <0与f≥0两种情况，分别计算f的递推公式。
算法中只有整数加减运算，效率很高。

三. 圆的扫描转换

圆的中点算法与椭圆的中点算法，采用类似的步骤。
直线是构成复杂图形的基本图元，场景中的模型往往由成千上万条直线组成，所以直线的中点算法是本章学习的重点，自定义CLine类来绘制直线段。

圆的扫描转换是在屏幕像素点阵中确定最佳逼近于理想圆的像素点集的过程。圆的绘制可以使用简单方程画圆算法或极坐标画圆算法，但这些算法涉及开方运算或三角运算，效率很低。主要讲解仅包含加减运算的顺时针绘制1/8圆的中点算法原理，根据对称性可以绘制整圆。

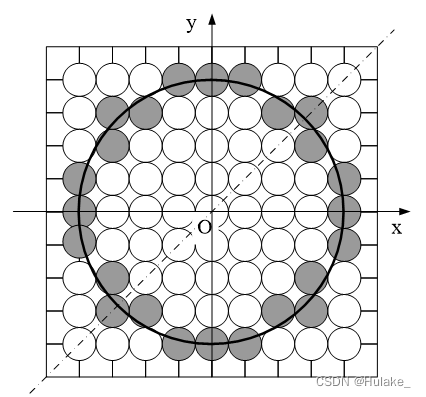
默认的圆是圆心位于坐标系原点，半径为R的圆。屏幕设备坐标系的原点位于左上角，绘制结果为1/4圆，需要进行圆心平移或使用自定义坐标系可以绘制整圆。
圆是椭圆的特例，使用椭圆中点算法也可绘制。

圆的中点算法:

void CTestView::MBCircle(double R,CDC *pDC)//圆的中点算法
{
	double x,y,d;	 
	d=1.25-R;x=0;y=R; //可用d=1-R计算d
	for(x=0;x<=y;x++)
	{
		CirclePoint(x,y,pDC);//画圆子函数，统一各变量值的位置
                       if (d<0)
			d+=2*x+3;
                       else
		{
			d+=2*(x-y)+5;
			y--;
		} 
     }
}

八分法画圆子函数:

void CTestView::CirclePoint(double x, double y,CDC *pDC)//八分法画圆子函数
{
	 //圆心坐标
            CP2 pc=CP2((p0.x+p1.x)/2.0,(p0.y+p1.y)/2.0);        
	 //定义圆的边界颜色 
            COLORREF  clr=RGB(0,0,255);                         
	pDC->SetPixelV(Round(x+pc.x),Round(y+pc.y),clr); //x,y
	pDC->SetPixelV(Round(y+pc.x),Round(x+pc.y),clr); //y,x
	pDC->SetPixelV(Round(y+pc.x),Round(-x+pc.y),clr);//y,-x
	pDC->SetPixelV(Round(x+pc.x),Round(-y+pc.y),clr);//x,-y
	pDC->SetPixelV(Round(-x+pc.x),Round(-y+pc.y),clr);//-x,-y
	pDC->SetPixelV(Round(-y+pc.x),Round(-x+pc.y),clr);//-y,-x
	pDC->SetPixelV(Round(-y+pc.x),Round(x+pc.y),clr);//-y,x
	pDC->SetPixelV(Round(-x+pc.x),Round(y+pc.y),clr);//-x,y
}

总结：

中点算法的优势在画圆算法中体现得更明显，用整数计算替换了平方开方等运算，算法效率提高更多。

四. 基本图形的扫描转换总结

直线、圆和椭圆作为二维场景中的基本图形，其生成算法的优劣对整个图形系统的效率至关重要。直线段的扫描转换是计算机图形学中最基本的算法。中点算法避免了复杂运算，使用了增量算法，使单点基本图形生成算法已无优化的余地，获得了广泛的应用。

五. 计算机图形学专栏

https://blog.csdn.net/weixin_53919192/category_11822648.html?spm=1001.2014.3001.5482https://blog.csdn.net/weixin_53919192/category_11822648.html?spm=1001.2014.3001.5482

原文链接：https://blog.csdn.net/weixin_53919192/article/details/124946915