引言
梯度下降:两个意思,
- 根据梯度(导数)的符号来判断最小值点x在哪;
- 让函数值下降(变小)。
简单来说就是一种寻找目标函数最小化的方法,它利用梯度信息,通过不断迭代调整参数来寻找合适的目标值。
其共有三种:
- BGD,batch gradient descent:批量梯度下降
- SGD,stochastic gradient descent:随机梯度下降
- mini-batch GD,mini-batch gradient descent:小批量梯度下降
BGD
假设有损失函数: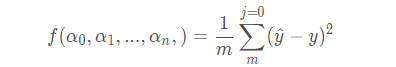
y ^ 是预测值,y是真实值,共有m个预测值。若要最小化损失函数,需要对每个参数α 0 , α 1 , . . . , α n 求梯度,但是对BGD通常是取所有训练样本损失函数的平均作为损失函数,假设有β 个样本,则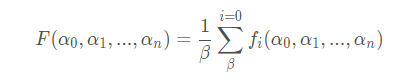
所以有梯度更新: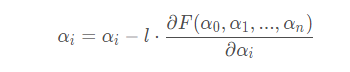
l为学习率,即步长,是一个经验值,过大容易找不到相对最优解,过小会使得优化速度过慢.
l后面是损失函数对参数αi求偏导数
优点:
- 一次迭代是对所有样本进行计算,此时利用矩阵进行操作,实现了并行。
- 由全数据集确定的方向能够更好地代表样本总体,从而更准确地朝向极值所在的方向。当目标函数为凸函数时,BGD一定能够得到全局最优。
缺点:
- 当样本数目 m 很大时,每迭代一步都需要对所有样本计算,训练过程会很慢。(有些样本被重复计算,浪费资源)
SGD
如果使用BGD会有一个问题,就是每次迭代过程中都要对几个样本进行求梯度,所以开销非常大,随机梯度下降的思想就是随机采样一个样本来更新参数,注意只是一个样本,大大的降低了计算开销。
为了简便计算,SGD每次迭代仅对一个样本计算梯度,直到收敛。伪代码如下(以下仅为一个loop,实际上可以有多个这样的loop,直到收敛):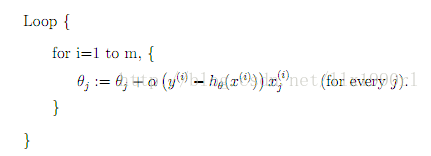
由于SGD每次迭代只使用一个训练样本,因此这种方法也可用作online learning。
每次只使用一个样本迭代,若遇上噪声则容易陷入局部最优解。
优点:
- 由于不是在全部训练数据上的损失函数,而是在每轮迭代中,随机优化某一条训练数据上的损失函数,这样每一轮参数的更新速度大大加快。
缺点:
- 准确度下降。由于即使在目标函数为强凸函数的情况下,SGD仍旧无法做到线性收敛。
- 可能会收敛到局部最优,由于单个样本并不能代表全体样本的趋势.
- 不易于并行实现。
mini-batch GD
SGD虽然提高了计算效率,降低了计算开销,但由于每次迭代只随机选择一个样本,因此随机性比较大,所以下降过程中非常曲折,效率也相应降低,所以mini-batch GD采取了一个折中的方法,每次选取一定数目(mini-batch)的样本组成一个小批量样本,然后用这个小批量来更新梯度,这样不仅可以减少计算成本,还可以提高算法稳定性。
从公式上似乎可以得出以下分析:速度比BGD快,比SGD慢;精度比BGD低,比SGD高。
优点:融合了BGD和SGD优点
- 通过矩阵运算,每次在一个batch上优化神经网络参数并不会比单个数据慢太多。
- 每次使用一个batch可以大大减小收敛所需要的迭代次数,同时可以使收敛到的结果更加接近梯度下降的效果。
- 可实现并行化。
基本最常用的就是mini-batch了 ,根据服务器性能选择合适的batch_size可以大大提高效率
三者的区别
