三次样条插值_深入插值算法（三次样条与埃尔米特）

一、差商

设节点为x₀,x₁,…,x_n则

x_i,x_j的一阶差商：

x_i,x_j,x_k的二阶差商：

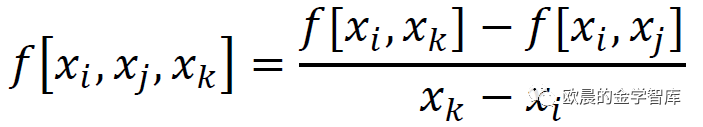
x₀,x₁,…,x_k的k阶差商：

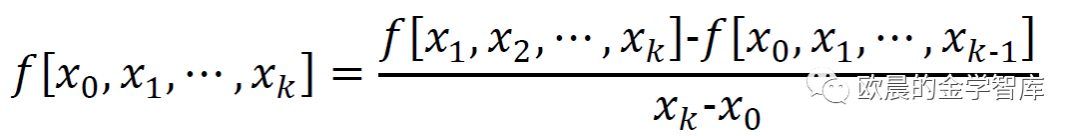
构建差商定义表：

注：这里构建差商是为了方便后续插值函数模型的构建。

import numpy as npimport numpy.linalg as lg#构建牛顿差商矩阵函数'''构建牛顿差商矩阵表x_val:对应x轴的数据；y_val:对应y轴的数据。'''def difference_quotient(x_val, y_val):    assert len(x_val) == len(y_val)     n = len(x_val)                   p = np.zeros((n, n+1))           p[:, 0] = x_val                  p[:, 1] = y_val                  for j in range(2, n+1):              p[j-1: n, j] = (p[j-1: n, j-1] - p[j-2: n-1, j-1]) / (x_val[j-1: n] - x_val[: n+1-j])        q = np.diag(p, k=1)    return p, q

二、三次样条插值

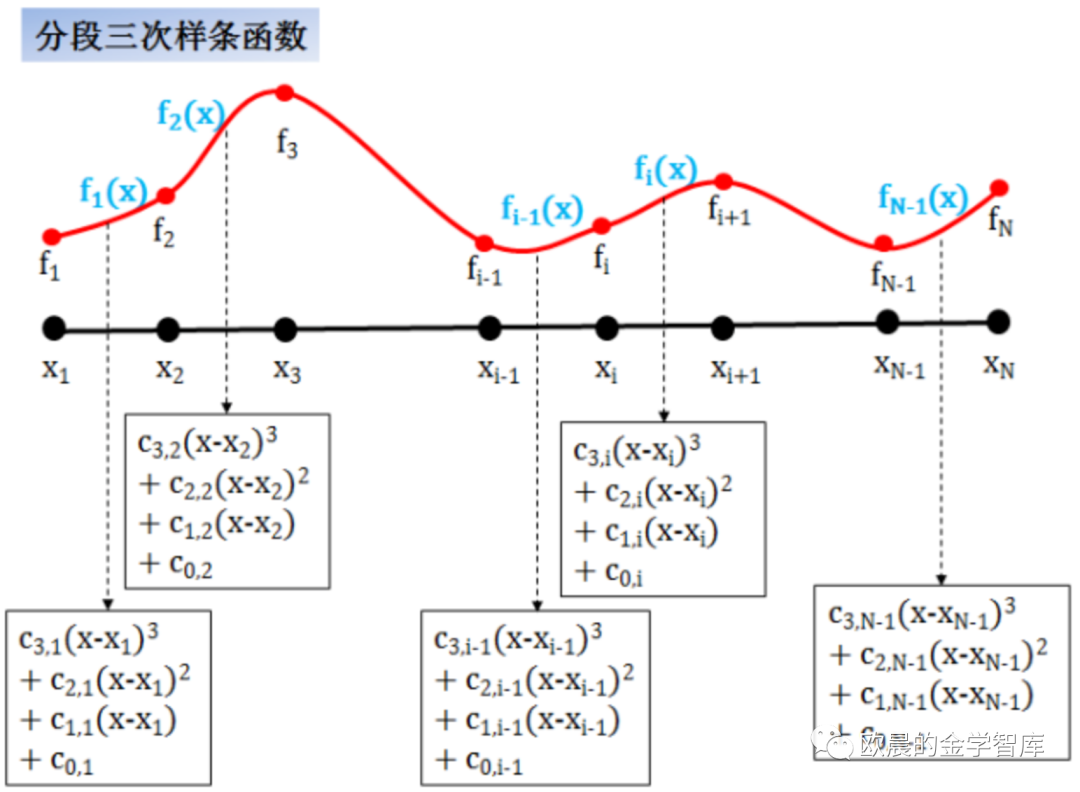
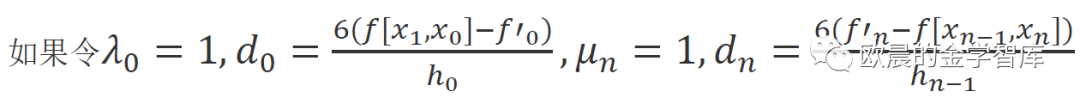
注：为了解决数据长度差异较大出现的抖动问题，我们通常将数据进行分段。比如0年-1年，1年-10年，>10年。

#构建三次样条插值函数'''构建三次样条插值函数x_val:对应原始x轴的数据；y_val:对应原始y轴的数据；x_interp：对应需要插值的x轴的点。'''    def cubic_spline_interp(x_val, y_val, x_interp):    x_lst = [x_interp] if isinstance(x_interp, (float, int)) else x_interp    x_loc = np.searchsorted(x_val, x_lst)        p, q = difference_quotient(x_val, y_val)  #调用差商函数        n = len(x_val) - 1    h_vec = x_val[1:] - x_val[:-1]    _u_vec = h_vec[-1:] / (h_vec[:-1] + h_vec[1:])    u_vec = _u_vec[1:]    lam_vec = 1 - u_vec        diag_mat = np.diag(u_vec, k=-1) + np.diag([2] * (n-1)) + np.diag(lam_vec, k=1)    d_vec = 6 * p[2:, 3]    m_vec = np.insert(np.append(lg.solve(diag_mat, d_vec), 0), 0, 0)        res_lst = []    for x, i in zip(x_lst, x_loc):        h_i = x_val[i] - x_val[i-1]        S_i = m_vec[i-1] * (x_val[i] - x) ** 3 / (6 * h_i) +\        m_vec[i] * (x - x_val[i-1]) ** 3 / (6 * h_i)+\        (y_val[i-1] - 1/6 * m_vec[i-1] * h_i ** 2) * (x_val[i] - x) / h_i+\        (y_val[i] - 1/6 * m_vec[i] * h_i ** 2) * (x - x_val[i-1]) / h_i        res_lst.append(S_i)            return res_lst

三、埃尔米特插值(中债登债券估值插值函数)

        埃尔米特(Hermite)插值又称带指定微商值的插值，也就是说，除了给出插值节点的函数值之外，还给出了指定插值节点的导数值。Hermite插值在插值节点处取相同的插值函数和导数值。

        可以构造2n+1次的Hermite插值多项式H(x)，并且H(x)是次数不超过2n+1次的插值多项式

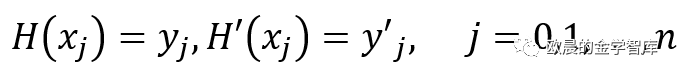
采用插值基函数的办法，构造如下插值函数

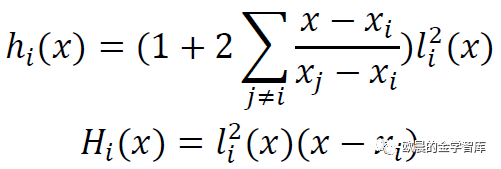
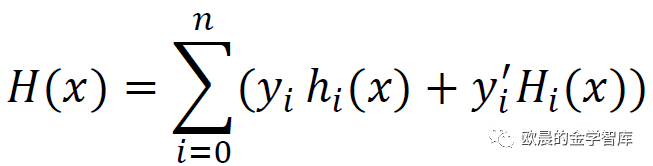
分段三次Hermite插值是按照分段插值的方法，把区间[a,b]分为若干个区间，在每个区间上使用三次Hermite插值。在各个节点上的插值基函数如下

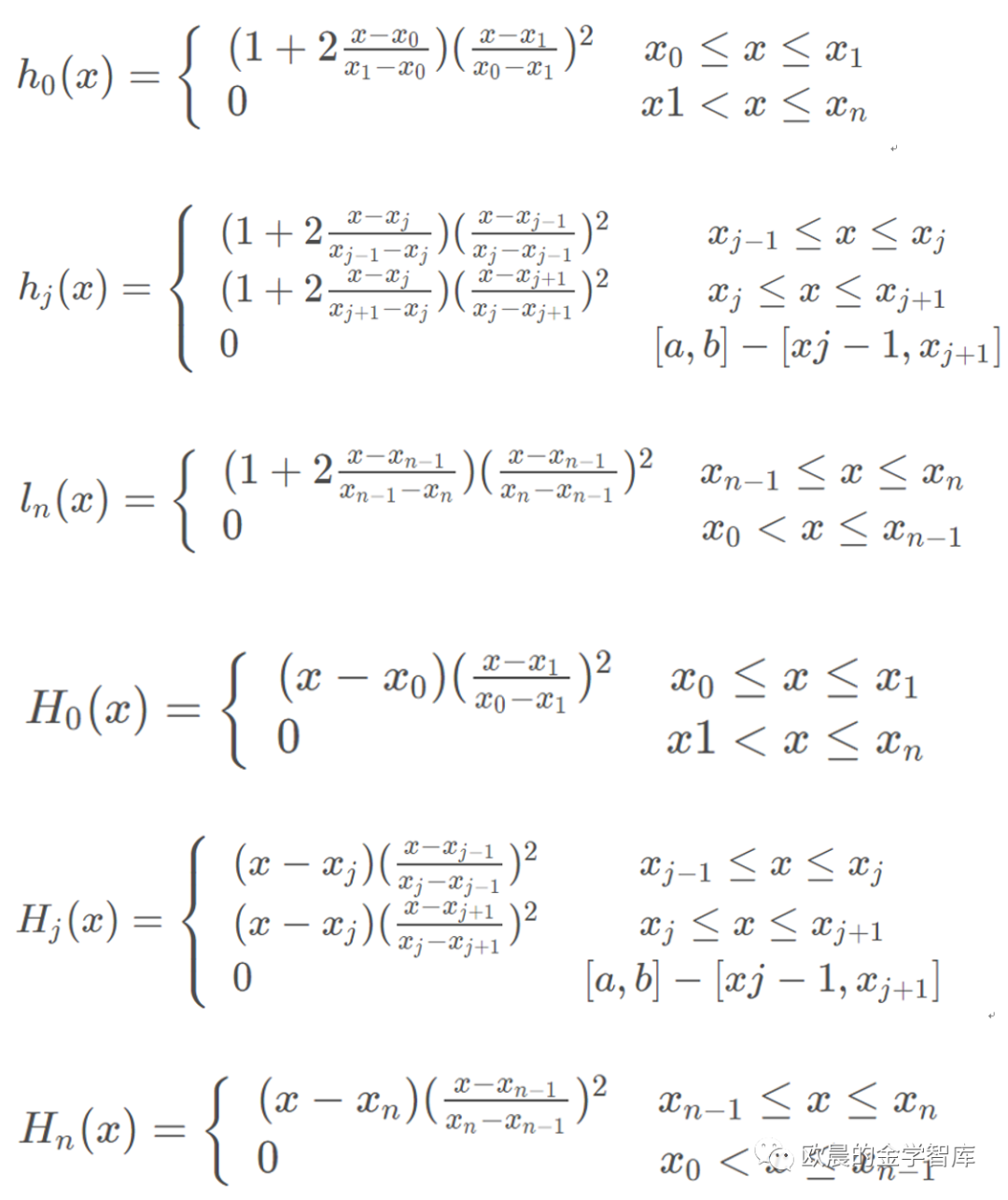
对于一阶导数的问题，我们可以简要用以下式子求解每个节点的一阶导数

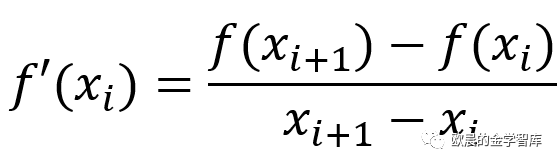
令最后一个节点的导数=0

#埃尔米特插值函数'''构建埃尔米特插值函数x_val:对应原始x轴的数据；y_val:对应原始y轴的数据；x_deriv：对应原始x轴数据的一阶导数；x_interp：对应需要插值的x轴的点。'''        def cubic_hermite_interp(x_val, y_val, x_deriv, x_interp):    x_lst = [x_interp] if isinstance(x_interp, (float, int)) else x_interp    x_loc = np.searchsorted(x_val, x_lst)    res_lst = []    for x, i in zip(x_lst, x_loc):        h_i = x_val[i] - x_val[i-1]        H_i = (1 + 2 * (x - x_val[i-1]) / h_i) * ((x - x_val[i]) / h_i) ** 2 * y_val[i-1] + \              (1 + 2 * (x_val[i] - x) / h_i) * ((x - x_val[i-1]) / h_i) ** 2 * y_val[i] + \              (x - x_val[i-1]) * ((x - x_val[i]) / h_i) ** 2 * x_deriv[i-1] + \              (x - x_val[i]) * ((x - x_val[i-1]) / h_i) ** 2 * x_deriv[i]                res_lst.append(H_i)        return res_lst

【案例分析】我们依旧以上节的国债收益率曲线为例，进行插值计算：

#分段三次埃尔米特插值k=deriv(maturity,ytm)   #端点处导数H1 = cubic_hermite_interp(maturity,ytm,k,matruity_new)   #获得分段三次埃尔米特插值函数#分段三次样条x1=maturity[0:5]  #分段为0-1y1=ytm[0:5] x2=maturity[4:10]  #分段为1-5y2=ytm[4:10]x3=maturity[9:]   #分段>5y3=ytm[9:]x1_=matruity_new[0:5]x2_=matruity_new[4:23]x3_=matruity_new[22:]ytm_new1=cubic_spline_interp(x1,y1,x1_)ytm_new2=cubic_spline_interp(x2,y2,x2_)ytm_new3=cubic_spline_interp(x3,y3,x3_)#画图import matplotlib.pyplot as pltfrom pylab import mplmpl.rcParams['font.sans-serif']=['SimHei']mpl.rcParams['axes.unicode_minus']=Falseplt.figure(figsize=(20,15))plt.plot(maturity,ytm,'b',label=u'线性',lw=1.5)plt.plot(matruity_new,H1,'r',label=u'埃尔米特插值',lw=1.5)#plt.plot(matruity_new,ytm_new,'g',label=u'三次样条插值',lw=1.5)plt.plot(x1_,ytm_new1,'g',label=u'三次样条插值',lw=1.5)plt.plot(x2_,ytm_new2,'g')plt.plot(x3_,ytm_new3,'g')plt.legend(fontsize=20)plt.grid('True')plt.show()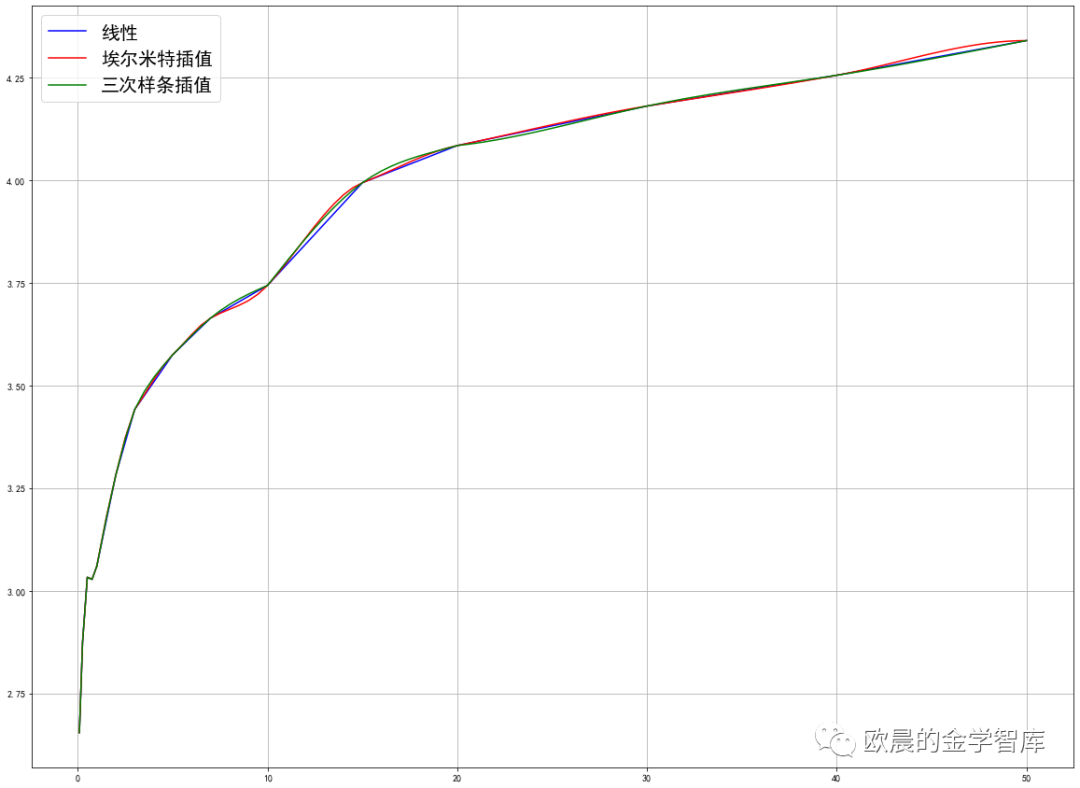

注：本篇对埃尔米特插值一阶导数的问题进行了简要构建，主要以应用为主，具体想看详细插值函数的可以参考以下内容：

https://blog.csdn.net/qq_36384657/article/details/98386776

2.https://zhuanlan.zhihu.com/p/63763725

附录：欢迎大家加好友，相互交流学习！

所有python案例分析的数据地址:链接：https://pan.baidu.com/s/1ds35rhd5yf-BSmzc-fxvzw提取码：je4a

点击可留言