JS实现优先队列

优先队列是一种特殊的队列，一般的队列，数据都是先进先出的，没有什么顺序。而优先队列不同，优先队列出队列的时候是具有优先级的，出队列的元素是优先级别最高的。（如最大值或者最小值），下面就以大顶堆为例实现一个优先队列。

预备知识

要实现优先队列前，需要先了解一些必要的知识，优先队列主要是基于二叉树来进行实现的，所以可以使用数组和链表实现，由于使用数据在内存上更具优势，本篇文章优先使用数组来实现一个优先队列。
那么就需要知道将数组映射到二叉树的一些基础知识，以数组[6, 5, 4, 1, 2, 3]为例，映射成二叉树就如下图所示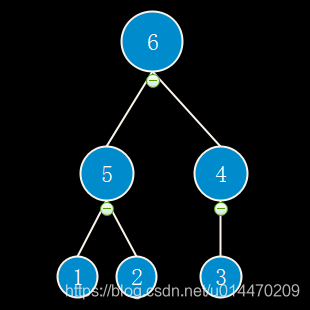

其实，就是，从上往下，从左往右依次排列，那么需要记住以下几点：

1. 最后一个非叶子节点(上图中为4)的下标为N/2 - 1向下取整
2. 第n个节点的左子节点和右子节点分别为2*n+1和2*n+2

然后我们需要实现的大顶堆就是父节点总是大于其子节点（上图中的二叉树就是一个大顶堆），那么可以知道根节点，也就是数组首位就是整个队列中的最大值，这在需要经常读取一堆大数据中的最大值的操作，非常有帮助，而且将根节点拿出，再重构一个大顶堆，再将根节点拿出，然后重构，直到队列为空，那么得到的就是一个从大到小排列的数据了，这就是堆排序。

大顶堆的构建

实现一个大顶堆的主要部分是要理解大顶堆的构建过程，简而言之就是，从最后一个非叶子节点开始，遍历到根节点(从下往上，从右往左)，将节点与左右子节点进行比较，如果改节点不是最大值，则将该节点与左右子节点中最大值进行交换，交换后，记住需要检查交换后的子节点的子树是否符合最大的规则。

我们以数组[1, 2, 3, 4, 5, 6]为例来演示下构建过程
首先数组映射到二叉树的结构如下图所示，最后一个非叶子节点为3，比较它和子节点的值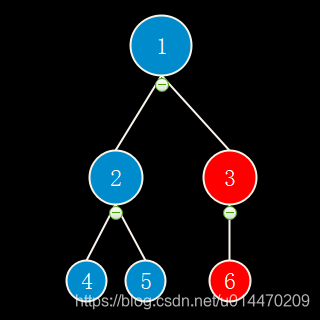

可以看到3 < 6所以交换两个节点位置后如下图：

然后比较节点2与其子节点的值：

发现5是最大的，所以交换节点2和节点5：

接着比较节点1与其子节点：

可以看到6最大，交换节点1和节点6：

节点1和节点6交换后，我们会发现节点1的位置不符合大顶堆的规则，那么我们需要再对节点1进行同样的调整

将节点1和节点3交换后，就构成了一个大顶堆：

我们把上面的步骤转化为代码后如下：

  init () {
    // 从倒数第一个非叶子节点（从下往上，从右往左数）依次重新排列节点顺序
    let lastParentNodeIndex = Math.floor(this.queue.length / 2) - 1
    for (let i = lastParentNodeIndex; i >= 0; i--) {
      this.buildChildNodes(i)
    }
  }

  buildChildNodes (index) {
    // 在数组中某个节点的左右子节点分别为 2*i+1 和 2*i+2
    // this.queue中存储着数组
    let arr = this.queue
    let left = index * 2 + 1
    let right = index * 2 + 2
    let maxIndex = index
    let length = arr.length

    // 找出值最大的节点下标
    if (left < length && arr[left] > arr[maxIndex]) {
      maxIndex = left
    }
  
    if (right < length && arr[right] > arr[maxIndex]) {
      maxIndex = right
    }

    if (maxIndex != index) {
      // 如果最大值不是父节点的话，需要交换父子节点位置
      // 并且对父节点交换后的子树递归地进行重新排列
      this.swap(index, maxIndex)
      this.buildChildNodes(maxIndex)
    }
  }

最重要的构造方法完成后我们来补充下大顶堆的一些其他方法。

大顶堆的其他方法补充

获取堆顶元素，也就是最大值peak方法，很简单，只要返回第一个元素即可：

peak () {
  return this.queue[0]
}

添加一个元素push方法，只需要往数组中push该元素，然后重新调整二叉树就行：

push (val) {
 this.queue.push(val)
  this.init()
}

出队列pop方法，pop方法可以仿照push方法，把数组第一个元素剔除后再重新调整二叉树，但把数组第一个元素剔除的操作是需要O(N)的时间复杂度的，所以，我们可以先保存数组第一个元素，然后将数组的最后一个元素pop出来赋值给第一个元素（时间复杂度为O(1)），然后再重新调整二叉树，并将保存的值返回：

pop () {
 // pop操作，就是将根节点拿出后，用最后一个节点填充根节点然后重新构建
  // 这样重新构建前的操作就是O(1)
  // 如果直接把根节点shift出去再重构建则，重新构建前的操作就是O(n)
  let val = this.queue[0]
  this.queue[0] = this.queue.pop()
  this.init()
  return val
}

将队列排序，也就是堆排序，因为上面的pop方法每次都会出队列一个最大值，所以只要pop N次就可以了：

sort () {
  // 排序的话就是把队列一个个pop出来
  var res = []
  var length = this.queue.length
  for (var i = 0; i < length; i++) {
    res.push(this.pop())
  }
  this.queue = res
  return res
}

完整代码

完整代码如下：

class PriorityQueue {
  constructor (arr = []) {
    this.queue = arr
    this.init()
  }

  init () {
    // 从倒数第一个非叶子节点（从下往上，从右往左数）依次重新排列节点顺序
    let lastParentNodeIndex = Math.floor(this.queue.length / 2) - 1
    for (let i = lastParentNodeIndex; i >= 0; i--) {
      this.buildChildNodes(i)
    }
  }

  buildChildNodes (index) {
    // 在数组中某个节点的左右子节点分别为 2*i+1 和 2*i+2
    let arr = this.queue
    let left = index * 2 + 1
    let right = index * 2 + 2
    let maxIndex = index
    let length = arr.length

    // 找出值最大的节点下标
    if (left < length && arr[left] > arr[maxIndex]) {
      maxIndex = left
    }
  
    if (right < length && arr[right] > arr[maxIndex]) {
      maxIndex = right
    }

    if (maxIndex != index) {
      // 如果最大值不是父节点的话，需要交换父子节点位置
      // 并且对父节点交换后的子树递归地进行重新排列
      this.swap(index, maxIndex)
      this.buildChildNodes(maxIndex)
    }
  }

  peak () {
    return this.queue[0]
  }

  push (val) {
    this.queue.push(val)
    this.init()
  }

  pop () {
    // pop操作，就是将根节点拿出后，用最后一个节点填充根节点然后重新构建
    // 这样重新构建前的操作就是O(1)
    // 如果直接把根节点shift出去再重构建则，重新构建前的操作就是O(n)
    let val = this.queue[0]
    this.queue[0] = this.queue.pop()
    this.init()
    return val
  }

  sort () {
    // 排序的话就是把队列一个个pop出来
    var res = []
    var length = this.queue.length
    for (var i = 0; i < length; i++) {
      res.push(this.pop())
    }
    this.queue = res
    return res
  }

  swap (index1, index2) {
    var arr = this.queue
    ;[arr[index1], arr[index2]] = [arr[index2], arr[index1]]
  }
}

也欢迎到我的github上查看