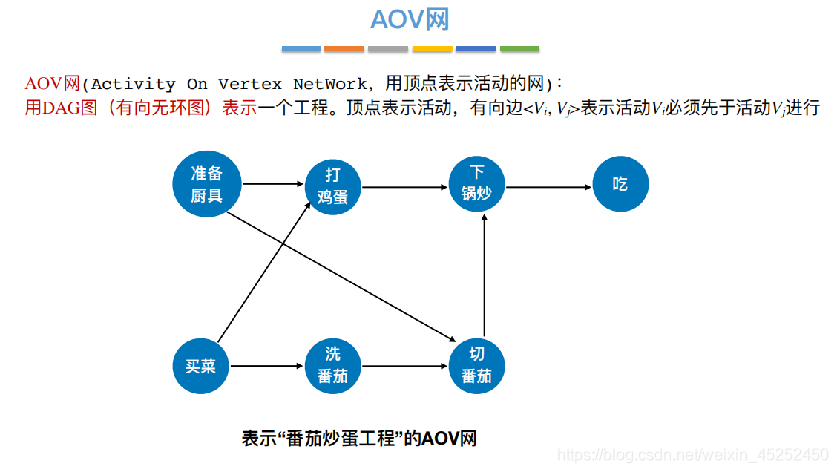
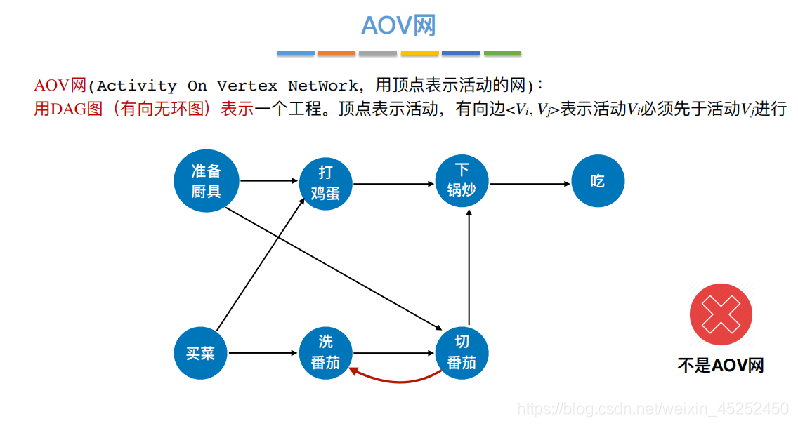
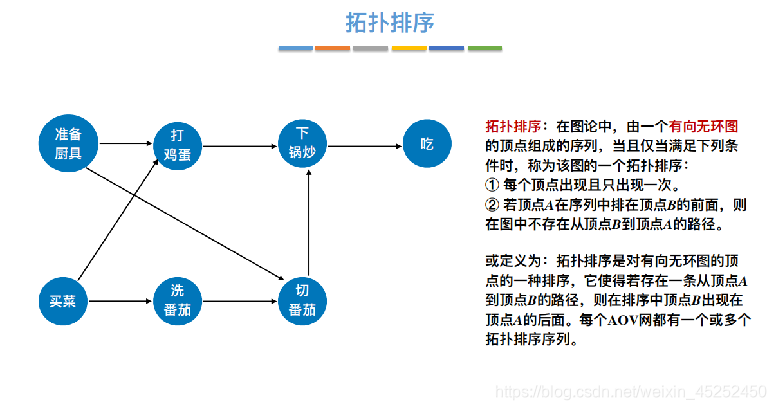
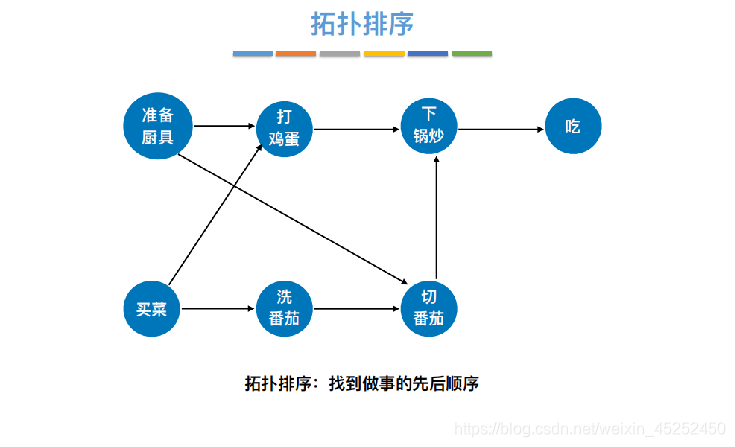
拓扑排序

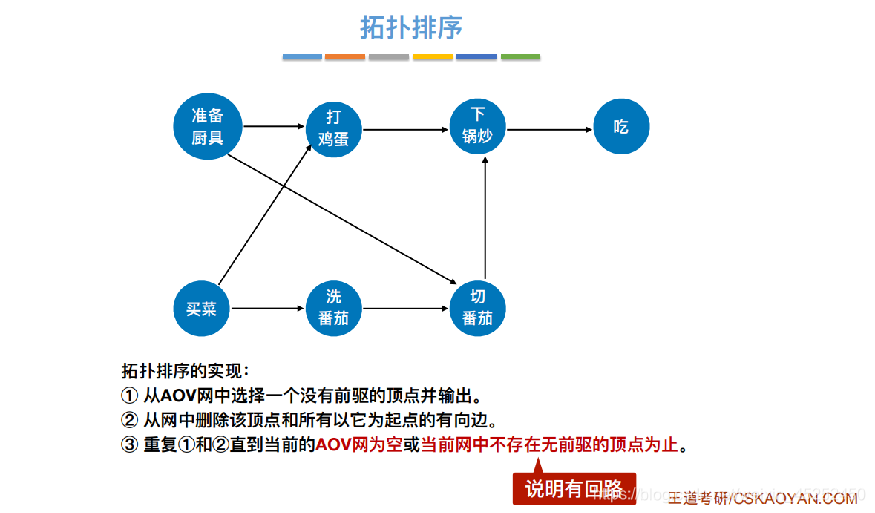
实现逻辑

用邻接表表示图

#include <iostream>
#include <stack>
#include <queue>
#include <vector>
#include <vector>
#include <algorithm>
#include <string.h>
using namespace std;
const int MaxVertexNum=10;
struct edgeListNode
{
  int adjId;
  int weight;
  edgeListNode* nextedge=nullptr; 
};
struct vertexListNode
{
  int data;
  edgeListNode* firstedge=nullptr;
};
struct Graph
{
  int vertexnum=0;
  int edgenum=0;
  vertexListNode vertexList[MaxVertexNum];
};
void InsertEdge(Graph& graph,int i,int j)
{
  edgeListNode* edge=new edgeListNode;
  edge->adjId=j;
  edge->nextedge=graph.vertexList[i].firstedge;//头插
  graph.vertexList[i].firstedge=edge;
}
void GraphInitiation(Graph& graph)
{
  graph.vertexnum=5;
  graph.edgenum=5;
  for(int i=0;i<graph.vertexnum;i++)//顶点表初始化
    graph.vertexList[i].data=i;
  vector<vector<int>>M={{0,1},{1,3},{2,3},{2,4},{3,4}};
  for(int i=0;i<M.size();i++)//边表初始化
    InsertEdge(graph,M[i][0],M[i][1]);
  for(int i=0;i<graph.vertexnum;i++)
  {
    printf("%d",graph.vertexList[i].data);
    edgeListNode* edge=graph.vertexList[i].firstedge;
    if(edge)
        printf("-->");
    while(edge)
    {
      printf("%d",graph.vertexList[edge->adjId]);
      edge=edge->nextedge;
      if(edge)
        printf("-->");
    }
    printf("\n");
  }
}

拓扑排序

unsigned int CalIndegree(Graph& graph,int v)
{
  uint cnt=0;
  for(int i=0;i<graph.vertexnum && i!=v;i++)
  {
    edgeListNode* edge=graph.vertexList[i].firstedge;
    while(edge)
    {
      if(edge->adjId==v)
        cnt++;
      edge=edge->nextedge;
    }
  }
  return cnt;
}
bool ToPoSort(Graph& graph)
{
  queue<int>Q;
  uint Indegree[graph.vertexnum];
  for(int i=0;i<graph.vertexnum;i++)
    if(!(Indegree[i]=CalIndegree(graph,i)))
      Q.push(i);
  uint cnt=0;
  while(!Q.empty())
  {
    int k=Q.front();
    Q.pop();
    cnt++;
    printf("%d ",k);
    for(edgeListNode* edge=graph.vertexList[k].firstedge;edge;edge=edge->nextedge)
    {
      int v=edge->adjId;
      if(!(Indegree[v]=Indegree[v]-1))
        Q.push(v);
    }
  }
  if(cnt<graph.vertexnum)
    return 0;
  else 
    return 1;
}

测试

int main()
{
  Graph graph;
  GraphInitiation(graph);
  printf("拓扑排序是：");
  ToPoSort(graph);
  printf("\n");
}

运行结果

0-->1
1-->3
2-->4-->3
3-->4
4
拓扑排序是：0 2 1 3 4 

逆拓扑排序

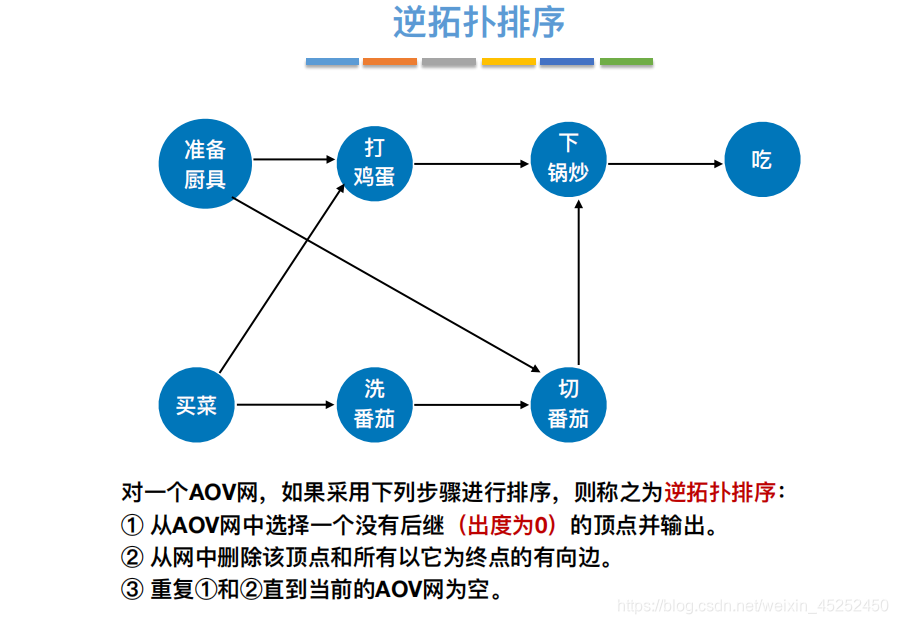
算法一（类似拓扑排序）：

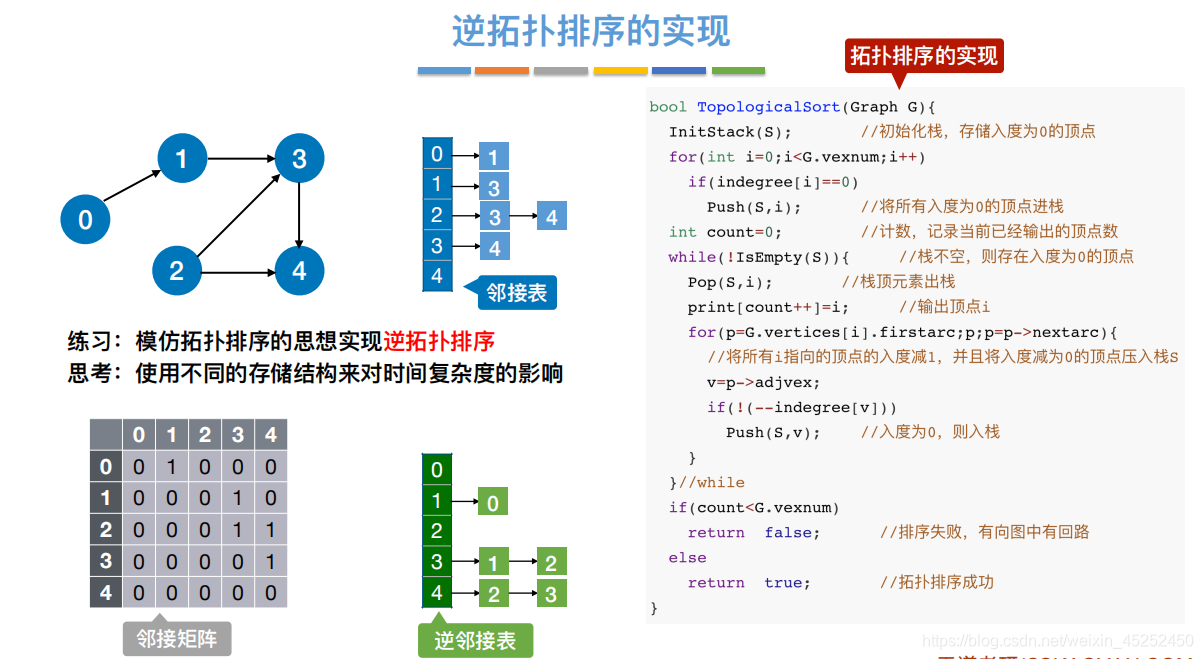
代码

unsigned int CalOutdegree(Graph& graph,int v)
{
  uint cnt=0;
  edgeListNode* edge=graph.vertexList[v].firstedge;
  while(edge)
  {
    cnt++;
    edge=edge->nextedge;
  }
  return cnt;
}
bool ToPoSort(Graph& graph)
{
  queue<int>Q;
  uint Outdegree[graph.vertexnum];
  for(int i=0;i<graph.vertexnum;i++)
    if(!(Outdegree[i]=CalOutdegree(graph,i)))
      Q.push(i);
  uint cnt=0;
  while(!Q.empty())
  {
    int k=Q.front();
    Q.pop();
    cnt++;
    printf("%d ",k);
    for(int i=0;i<graph.vertexnum && i!=k;i++)
    {
      edgeListNode* edge=graph.vertexList[i].firstedge;
      while(edge)
      {
        if(edge->adjId==k)
        {
          Outdegree[i]=Outdegree[i]-1;
          if(!Outdegree[i])
            Q.push(i);
          break;
        }
        edge=edge->nextedge;
      }
    }
  }
  if(cnt<graph.vertexnum)
    return 0;
  else 
    return 1;
}
int main()
{
  Graph graph;
  GraphInitiation(graph);
  printf("逆拓扑排序是：");
  ToPoSort(graph);
  printf("\n");
}

运行结果

0-->1
1-->3
2-->4-->3
3-->4
4
逆拓扑排序是：4 3 1 2 0 

算法二（深度搜索）：

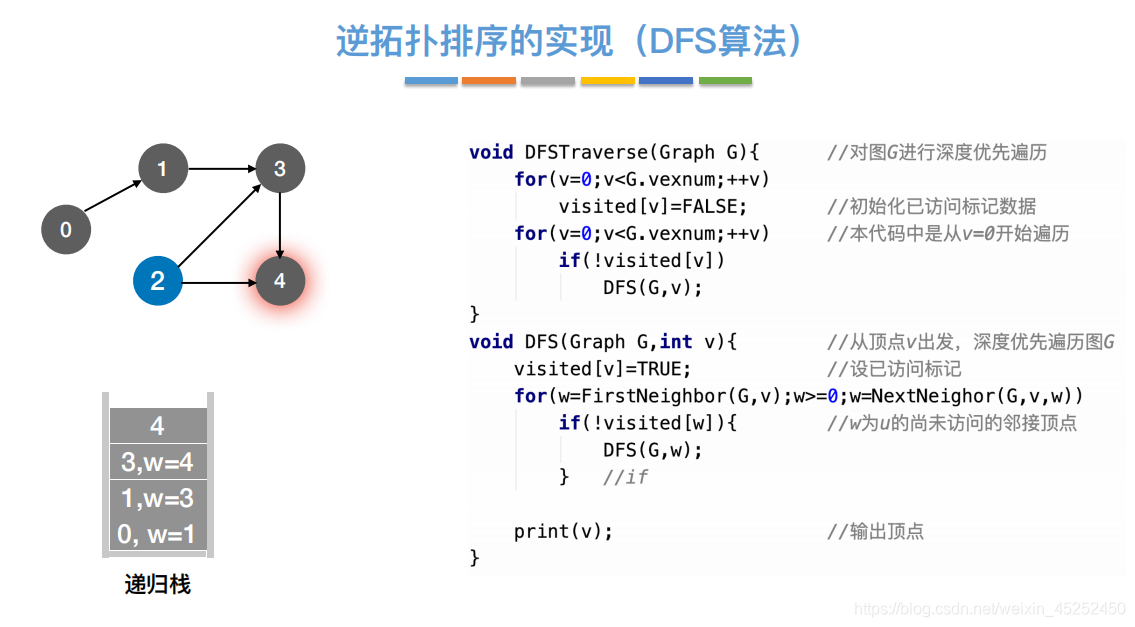
void dfs(Graph& graph,bool* visited,int v)
{
  visited[v]=true;
  edgeListNode* edge=graph.vertexList[v].firstedge;
  if(edge)
  {
    if(!visited[edge->adjId])
      dfs(graph,visited,edge->adjId);
    edge=edge->nextedge;
  }
  printf("%d ",v);
}
void ToPoSort_DFS(Graph& graph,bool* visited)
{
  for(int i=0;i<graph.vertexnum;i++)
    if(!visited[i])
      dfs(graph,visited,i);
}
int main()
{
  Graph graph;
  GraphInitiation(graph);
  bool visited[graph.vertexnum];
  memset(visited,0,graph.vertexnum);
  printf("逆拓扑排序为：");
  ToPoSort_DFS(graph,visited);
  printf("\n");
}

运行结果

0-->1
1-->3
2-->4-->3
3-->4
4
逆拓扑排序为：4 3 1 0 2