贪心思想——区间选点

分析：

区间选点问题描述：给出若干个区间，选取最少的点，使得每个区间内都至少有一个点

做法：先对所有区间的右端点b进行排序（由小到大），然后选取第一个b，作为选取的第一个点，然后对包含这个点的区间进行标记；再选取未标记的区间内最小的b，如此循环…直到所有区间都标记了。
贪心点就是，选取最右边的点b。

简要理解一下这样做法的正确性：（证明反命题为假）
对于已经根据b排好序的区间，如果选取的点不是b，而是[a,b-1]里面的任意数，该点过的区间<=b点过的区间。如下图，如果选择的不是b，那么在这一次选择中，就没有包含到区间2，这一个选取步骤就劣于选取b。每步都落后，最终的结果不可能比选取b更好。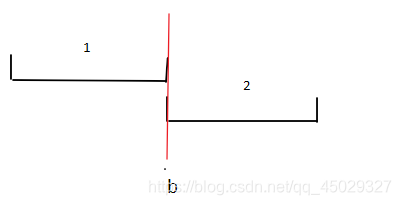

具体问题：

数轴上有 n 个闭区间 [a_i, b_i]。取尽量少的点，使得每个区间内都至少有一个点（不同区间内含的点可以是同一个）

input:
第一行1个整数N（N<=100）
第2~N+1行，每行两个整数a,b（a,b<=100）
output:
一个整数，代表选点的数目

全部代码：

#include<stdio.h>
#include<algorithm>
using namespace std;
int visit[100];//记录区间是否包含过取得的点
int N;
struct space
{
	int a;
	int b;
	bool operator < (const space &n) const{
		return b<n.b;//按照b升序
	}
}spa[100];
void biaoji(int now)
{
	for(int i=0;i<N;i++)
	{
		if(visit[i]==0 && spa[i].a<=now)
			visit[i]=1;
	}
}
int main()
{
	int now,count=0;
	scanf("%d",&N);//N个区间
	for(int i=0;i<N;i++)
		scanf("%d %d",&spa[i].a,&spa[i].b);
	//按照b进行排序
	sort(spa,spa+N);
	//首先取的点是spa[0].b这个点，然后看覆盖了多少区间，再次取未覆盖的b
	for(int i=0;i<N;i++)
	{
		if(visit[i]==0)
		{
			now=spa[i].b;count++;
			//标记这个点所有的区间
			biaoji(now);
		}
	}
	printf("%d\n",count);
	return 0;
}