1.核函数的目的
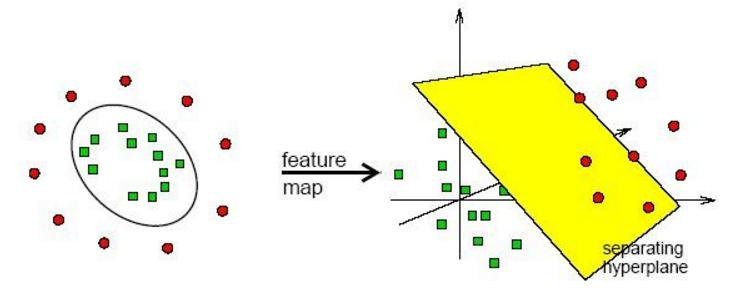
如果我的数据有足够多的可利用的信息,我就能够充分学习这些数据去拟合特定事务的特征了,但是现在如果没有那么多的信息,我们可不可以在数学上进行一些投机呢?比如,我们将数据从低维变换到高维。如下图所示,如果在二维情况下,我们很难通过建模做出分类,因为需要建立一个环去分离数据,但是通过三维变换,我们就能很轻松的用一个平面做出分类。
2.线性核函数
Linear核函数对数据不做任何变换。![]()
特征已经比较丰富了,样本数据量巨大,需要进行实时得出结果的问题。不需要设置任何参数,直接就可以用了。
3.多项式核函数
需要给定3个参数![]()
一般情况下2次的更常见![]()
4.核函数实例
对于核函数,我们真的是先将每个实例映射到高维在做内积吗?很明显,当特征数比较多的时候,运算量十分庞大。我们发现,先做内积在做核函数变换与先做核函数变换再做内积,其结果是一致的,对于运算量,很明显,对一个数做核函数变换的运算量远远小于分别对向量做核函数变换。

5.高斯核函数
一维度的高斯![]()
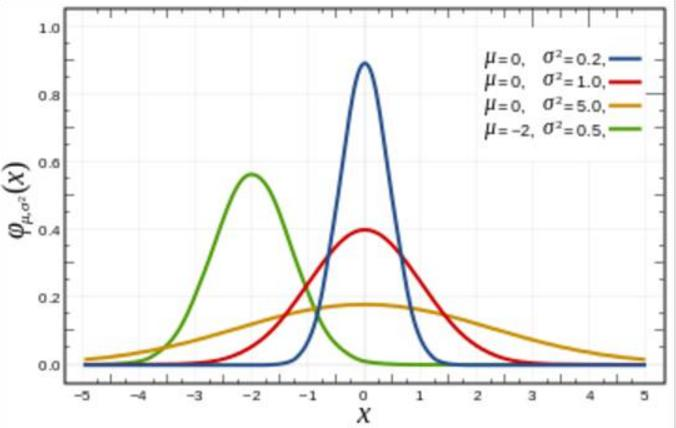
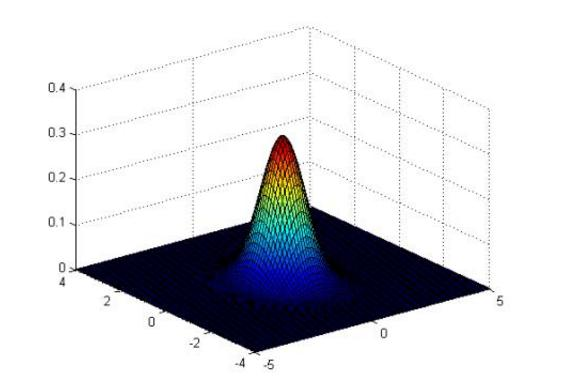
二维的高斯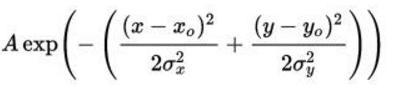
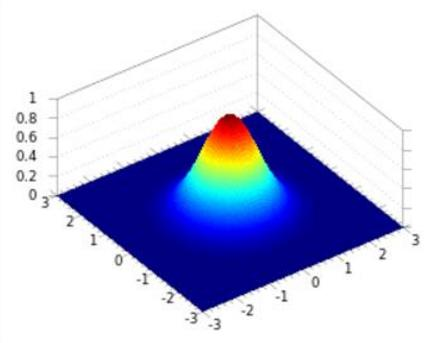
高斯核函数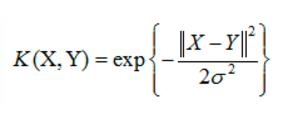
如果X和Y很相似,那结果也就是1,如果很不相似那就是0。
高斯核函数能给我做出多少维特征呢?我们对高斯和函数进行泰勒展开,化简后发现我们可以得到无穷维的特征。
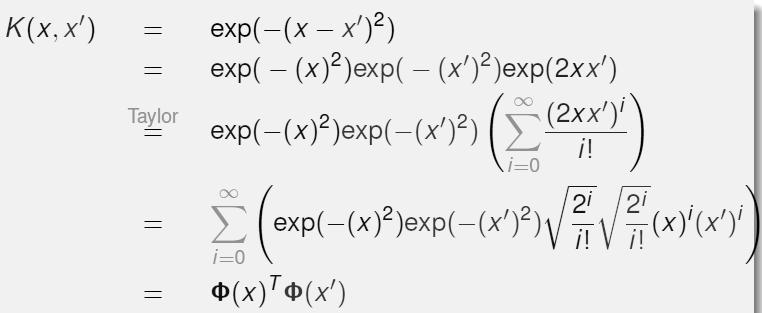
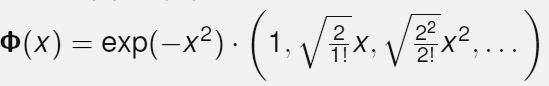
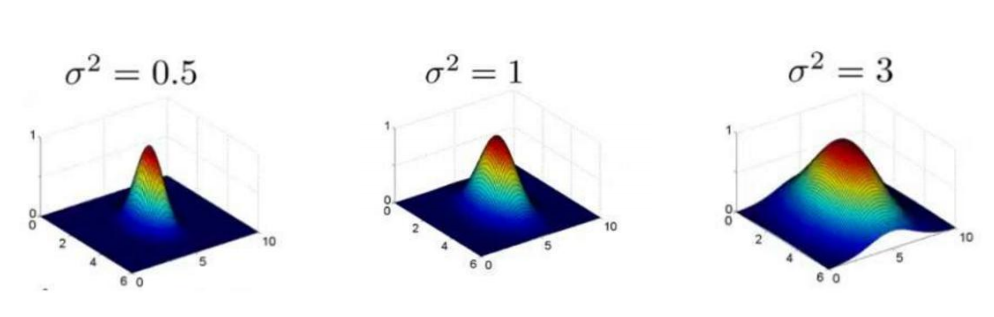
参数的影响:

但是它对参数是极其敏感的,效果差异也是很大的,越小,差异越显著

6.熵
熵表示物体内部的混乱程度。(一件事发生的不确定性)
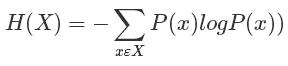
所有的概率值都是0-1之间,那么最终的H(X)必然也是一个正数
熵值的意义:
熵值高,选择的概率低,不确定性很高,类似于杂货铺
熵值低,选择的概率高,不确定性低,类似于苹果专卖店。
熵值越低,分类效果越好。
7.sigmoid函数
非线性:让模型表现能力更强
单调性,可微性,输出值范围是有限的
常见的激活函数:Sigmoid Tanh Relu 等
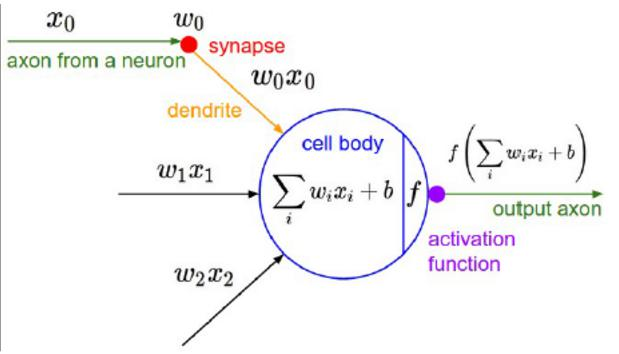
Sigmoid函数
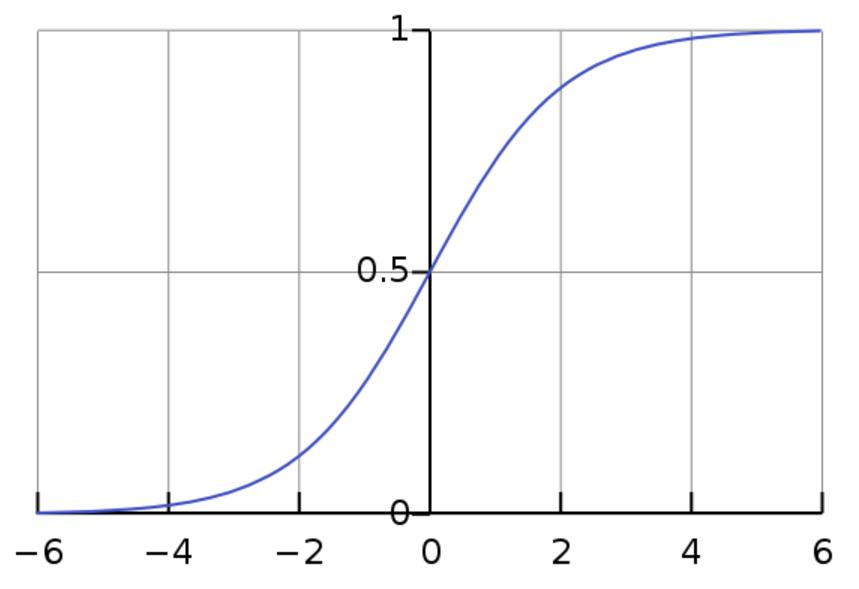
输出值全为整数会导致梯度全为正或者全为负
优化更新会产生阶梯式情况

Tanh函数
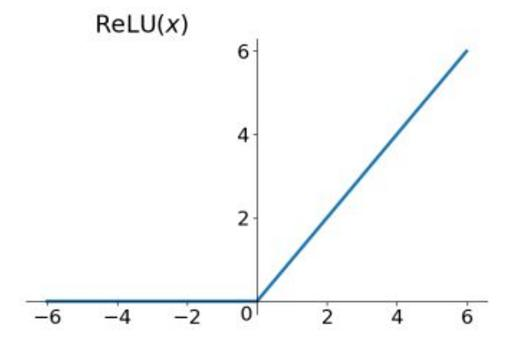
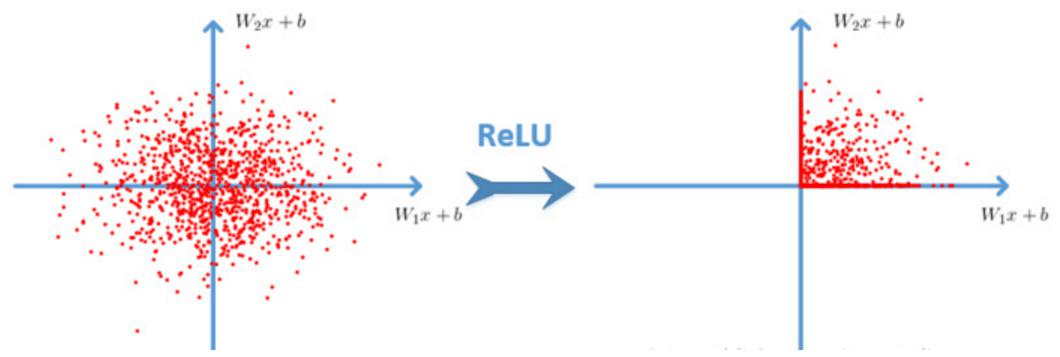
Relu函数
公式简单实用、解决了梯度消失现象,计算速度更快