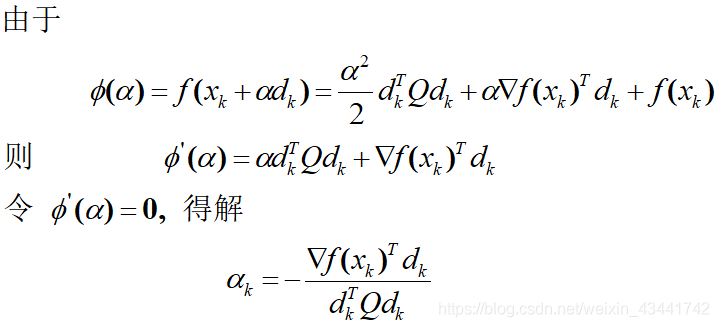在上节中本教程介绍了迭代搜索的基本步骤。考虑基本步骤中的每一步的基本元素:步长、下降方向和终止准则,其中终止准则是我们已经明确给出的,而步长和下降方向可以是任意的。但任意并不代表随机,一个随机的迭代搜索算法是无法保证收敛性的。步长和下降方向需要我们针对每一步搜索到的点的情况来求解,不仅要保证算法的收敛性,还要使得算法具有尽可能快的收敛速度。
在本节中本教程将介绍迭代搜索过程中步长的计算方法,而下降方向的计算方法会在接下来几节内给出。
1 步长的精确搜索
若我们已经知道了一个下降方向d k d_kdk,就只需要求参数α \alphaα使其满足一维优化问题m i n f ( x k + α d k ) minf(x_k+\alpha d_k)minf(xk+αdk)的解,令ϕ ( α ) = f ( x k + α d k ) \phi(\alpha)=f(x_k+\alpha d_k)ϕ(α)=f(xk+αdk),则ϕ ′ ( α ) = ∇ f ( x k + α d k ) T d k = 0 \phi'(\alpha)=\nabla f(x_k+\alpha d_k)^Td_k=0ϕ′(α)=∇f(xk+αdk)Tdk=0,求解该线性方程组即可。
对于简单的方程,精确搜索是非常快速有效甚至有现成结论的。例如对于任意二次函数1 2 x T G x + c ( x ) \frac{1}{2}x^TGx+c(x)21xTGx+c(x)(黑森矩阵G中值任意所以可以表示任意二次函数),有α = − ∇ f ( x ) T d d T G d \alpha=-\frac{\nabla f(x)^T d}{d^TGd}α=−dTGd∇f(x)Td。(证明见附录)
但我们知道,计算机求解线性方程组的方法是高斯消元法,这是一个时间复杂度为o ( n 3 ) o(n^3)o(n3)的算法。不仅对于高维情况耗时长,就算是低维情况、单次求解的耗时可以忍受,当我们把求步长的算法整合进整个迭代算法体系中、在每次迭代时都求解步长时,积累起来就是一个巨大的时间开销。所以,如果目标函数较为复杂,我们不能得出与任意二次函数的步长求解相似的结论时,我们通常使用非精确搜索。
2 步长的非精确搜索
2.1 Armijo线搜索
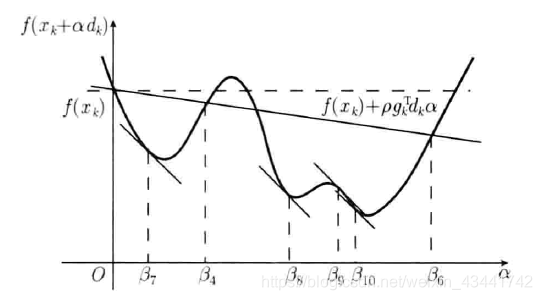
考虑泰勒展开f ( x k + α k d k ) = f ( x k ) + α k g k T d k + o ( ∣ ∣ α k d k ∣ ∣ 2 ) f(x_k+\alpha_kd_k)=f(x_k)+\alpha_kg^T_kd_k+o(||\alpha_kd_k||^2)f(xk+αkdk)=f(xk)+αkgkTdk+o(∣∣αkdk∣∣2),去掉极小项,我们可以在x k x_kxk点处找到f ( x ) f(x)f(x)的一条切线s ( α ) = f ( x k ) + g k T d k α s(\alpha)=f(x_k)+g_k^Td_k \alphas(α)=f(xk)+gkTdkα
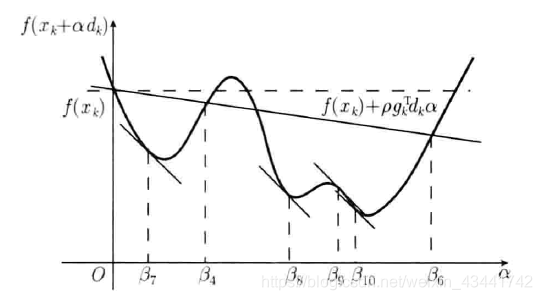
如图所示的曲线为d k d_kdk方向上函数的截线。结合图像不难理解,若局部为凸函数,则局部最优解出现在过x k x_kxk点平行于α \alphaα轴的直线与切线s ( α ) = f ( x k ) + g k T d k α s(\alpha)=f(x_k)+g_k^Td_k \alphas(α)=f(xk)+gkTdkα所夹范围之间
我们让s ( α ) s(\alpha)s(α)向着平行于α \alphaα轴的直线方向旋转一个角度得到s ′ ( α ) s'(\alpha)s′(α),使s ′ ( α ) s'(\alpha)s′(α)被s ( α ) s(\alpha)s(α)和平行于α \alphaα轴的直线所夹。其具体方法是在斜率上乘上一个0 < ρ < 1 0<\rho<10<ρ<1,那么如图红色部分的点比起x k x_kxk将更接近局部最优解。
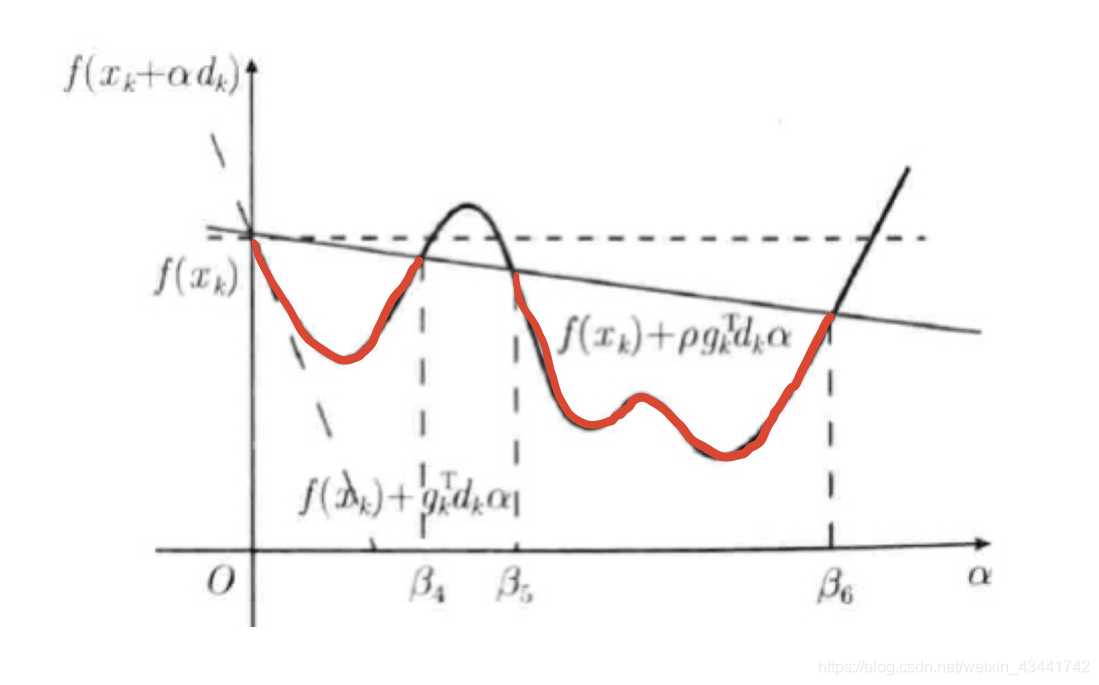
这样我们就使得函数的值在我们选取的方向上有了一定程度的下降。也许我们不能一次求出最优解,但只要我们不断迭代,并每次都保证搜索方向为下降方向,就能使得Armijo线搜索收敛到该方向上的一个局部最优解。
例如,考虑最基本的情况,若函数只存在d k d_kdk方向及其反方向,在红色部分选取任意一个点(比如下降方向上s ′ ( α ) s'(\alpha)s′(α)与f ( x k + α k d k ) f(x_k+\alpha_kd_k)f(xk+αkdk)的第一个交点)作为x k + 1 x_{k+1}xk+1,寻找下降方向并重复上述过程,最终就会以如图所示的形式收敛到最优解。
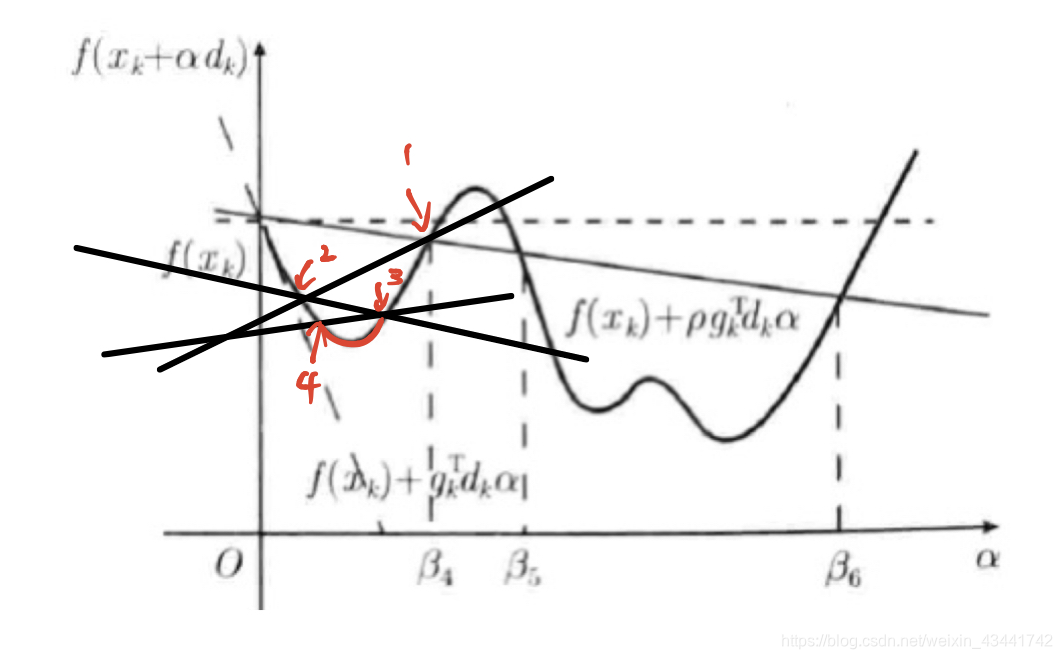
因此Armijo线搜索的关键在于找到一个位于红色区域内的点。其具体方法是先假设一个步长α \alphaα,若不满足Armijo线性搜索条件就缩短该步长,直到满足线性搜索条件。因为我们保证了s ′ ( α ) s'(\alpha)s′(α)的斜率小于s ( α ) s(\alpha)s(α),所以这样的步长必定是存在的,结合图像也不难理解。
Armijo线搜索条件:给定ρ ∈ ( 0 , 1 ) \rho\in(0,1)ρ∈(0,1),计算α k \alpha_kαk满足f ( x k + α k d k ) ≤ f ( x k ) + ρ α k ∇ f ( x k ) T d k f(x_k+\alpha_kd_k)\leq f(x_k)+\rho\alpha_k\nabla f(x_k)^Td_kf(xk+αkdk)≤f(xk)+ραk∇f(xk)Tdk
步骤:
- 选取一个参数ρ 1 ∈ ( 0 , 0.5 ) \rho_1 \in (0,0.5)ρ1∈(0,0.5)
- 取α k = 1 \alpha_k=1αk=1,若α k \alpha_kαk满足线性搜索条件,则得到α k \alpha_kαk
- 取α k = β > 0 \alpha_k=\beta>0αk=β>0,若α k \alpha_kαk满足线性搜索条件,则得到α k \alpha_kαk
- 取α k = ρ 1 α k \alpha_k=\rho_1 \alpha_kαk=ρ1αk
- 若α k \alpha_kαk满足线性搜索条件,则得到α k \alpha_kαk,否则转4
2.2 Wolfe-Powell搜索
在Armijo搜索的条件基础上增加防止步长过小的条件,使得x k + α k d k x_k+\alpha_kd_kxk+αkdk处曲线切线斜率∇ f ( x k + α k d k ) T d k \nabla f(x_k+\alpha_kd_k)^Td_k∇f(xk+αkdk)Tdk具有下界σ ∇ f ( x k ) T d k \sigma\nabla f(x_k)^Td_kσ∇f(xk)Tdk。在之后的教程中我们会提到,这使得算法收敛性得到保证。
为保证α k \alpha_kαk的存在性,通常取0 < σ < 1 2 0<\sigma<\frac{1}{2}0<σ<21
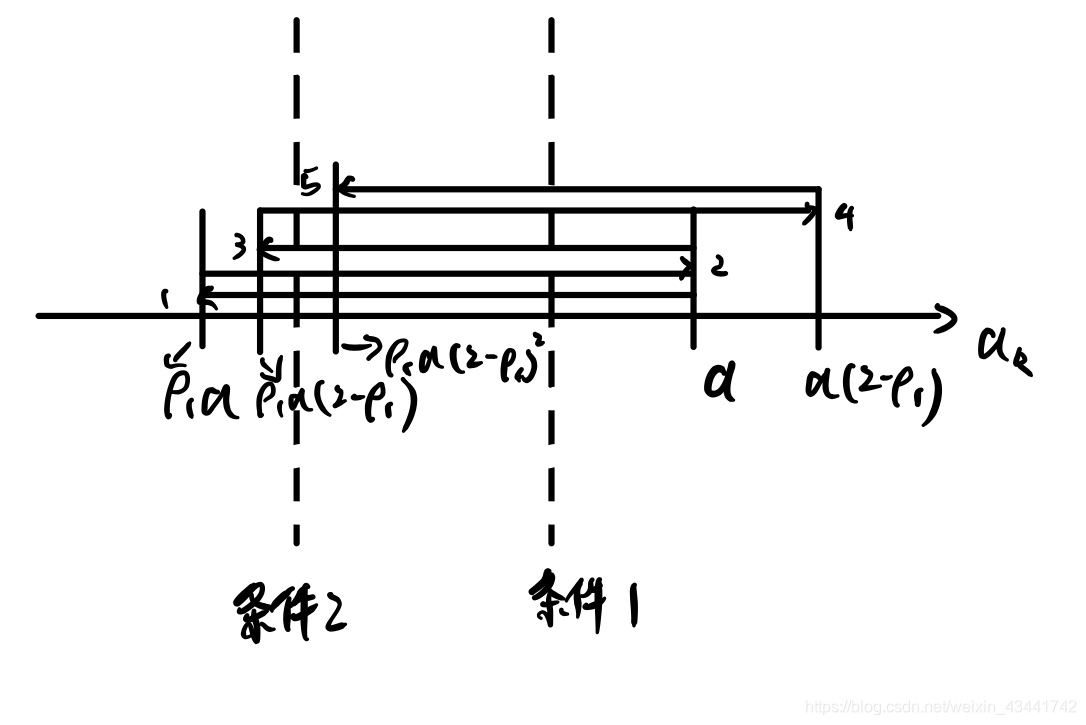
则有Wolfe-Powell线搜索条件:给定ρ ∈ ( 0 , 1 ) , σ ∈ ( 0 , 1 2 ) \rho\in(0,1),\sigma\in(0,\frac{1}{2})ρ∈(0,1),σ∈(0,21),计算α k \alpha_kαk满足{ f ( x k + α k d k ) ≤ f ( x k ) + ρ α k ∇ f ( x k ) T d k ∇ f ( x k + α k d k ) T d k ≥ σ ∇ f ( x k ) T d k \begin{cases}f(x_k+\alpha_kd_k)\leq f(x_k)+\rho\alpha_k\nabla f(x_k)^Td_k\\\nabla f(x_k+\alpha_kd_k)^Td_k\geq \sigma\nabla f(x_k)^Td_k\end{cases}{f(xk+αkdk)≤f(xk)+ραk∇f(xk)Tdk∇f(xk+αkdk)Tdk≥σ∇f(xk)Tdk
步骤:
- 若α k = 1 \alpha_k=1αk=1满足Wolfe-Powell线搜索条件,则取α k = 1 \alpha_k=1αk=1
- 给定常数β > 0 \beta>0β>0,ρ 1 ∈ ( 0 , 1 ) \rho_1\in(0,1)ρ1∈(0,1),令α k ( 0 ) \alpha_k^{(0)}αk(0)是集合{ β ρ 1 j } \{\beta\rho_1^j\}{βρ1j}中满足条件1的最大者,令i=0
- 若α k ( i ) \alpha_k^{(i)}αk(i)满足条件2,则取α k = α k ( i ) \alpha_k=\alpha_k^{(i)}αk=αk(i),否则令β k = ρ 1 − 1 α k ( i ) \beta_k=\rho^{-1}_1\alpha_k^{(i)}βk=ρ1−1αk(i)
- 令α k ( i + 1 ) \alpha_k^{(i+1)}αk(i+1)是集合{ α k ( i ) + ρ 1 j ( β k ( i ) − α k ( i ) ) , j = 0 , 1 , 2... } \{\alpha_k^{(i)}+\rho_1^j(\beta_k^{(i)}-\alpha_k^{(i)}),j=0,1,2...\}{αk(i)+ρ1j(βk(i)−αk(i)),j=0,1,2...}中满足条件1的最大者,令i = i + 1 i=i+1i=i+1,转步3
这个搜索过程可以直观地使用下图理解:
2.3 强条件的Wolfe-Powell搜索
在Wolfe-Powell搜索的条件基础上增加防止步长过大的条件,使得x k + α k d k x_k+\alpha_kd_kxk+αkdk处曲线切线斜率∇ f ( x k + α k d k ) T d k \nabla f(x_k+\alpha_kd_k)^Td_k∇f(xk+αkdk)Tdk具有上界− σ ∇ f ( x k ) T d k -\sigma\nabla f(x_k)^Td_k−σ∇f(xk)Tdk,也就是说条件转化为了:给定ρ ∈ ( 0 , 1 ) , σ ∈ ( 0 , 1 2 ) \rho\in(0,1),\sigma\in(0,\frac{1}{2})ρ∈(0,1),σ∈(0,21),计算α k \alpha_kαk满足{ f ( x k + α k d k ) ≤ f ( x k ) + ρ α k ∇ f ( x k ) T d k ∇ f ( x k + α k d k ) T d k ≥ σ ∇ f ( x k ) T d k ∇ f ( x k + α k d k ) T d k ≤ − σ ∇ f ( x k ) T d k \begin{cases}f(x_k+\alpha_kd_k)\leq f(x_k)+\rho\alpha_k\nabla f(x_k)^Td_k\\\nabla f(x_k+\alpha_kd_k)^Td_k\geq \sigma\nabla f(x_k)^Td_k\\\nabla f(x_k+\alpha_kd_k)^Td_k\leq -\sigma\nabla f(x_k)^Td_k\end{cases}⎩⎪⎨⎪⎧f(xk+αkdk)≤f(xk)+ραk∇f(xk)Tdk∇f(xk+αkdk)Tdk≥σ∇f(xk)Tdk∇f(xk+αkdk)Tdk≤−σ∇f(xk)Tdk
步骤:
- 若α k = 1 \alpha_k=1αk=1满足Wolfe-Powell线搜索条件,则取α k = 1 \alpha_k=1αk=1
- 给定常数β > 0 \beta>0β>0,ρ 1 ∈ ( 0 , 1 ) \rho_1\in(0,1)ρ1∈(0,1),令α k ( 0 ) \alpha_k^{(0)}αk(0)是集合{ β ρ 1 j } \{\beta\rho_1^j\}{βρ1j}中满足条件1和条件3的最大者,令i=0
- 若α k ( i ) \alpha_k^{(i)}αk(i)满足条件2,则取α k = α k ( i ) \alpha_k=\alpha_k^{(i)}αk=αk(i),否则令β k = ρ 1 − 1 α k ( i ) \beta_k=\rho^{-1}_1\alpha_k^{(i)}βk=ρ1−1αk(i)
- 令α k ( i + 1 ) \alpha_k^{(i+1)}αk(i+1)是集合{ α k ( i ) + ρ 1 j ( β k ( i ) − α k ( i ) ) , j = 0 , 1 , 2... } \{\alpha_k^{(i)}+\rho_1^j(\beta_k^{(i)}-\alpha_k^{(i)}),j=0,1,2...\}{αk(i)+ρ1j(βk(i)−αk(i)),j=0,1,2...}中满足条件1和条件3的最大者,令i = i + 1 i=i+1i=i+1,转步3
一般情况下的步长计算问题,只需要用普通的Wolfe-Powell搜索即可。而强条件的Wolfe-Powell搜索则在一些特殊的下降算法中有用武之地,这在我们之后的教程中会提到。
代码实现
本博客所有代码在https://github.com/HarmoniaLeo/optimization-in-a-nutshell开源,如果帮助到你,请点个star,谢谢这对我真的很重要!
你可以在上面的GitHub链接或本文集的第一篇文章深入浅出最优化(1) 最优化问题概念与基本知识中找到Function.py和lagb.py
Armijo线搜索:
import numpy as np
from Function import Function #定义法求导工具
from lagb import * #线性代数工具库
#假设d已经给出
a=1 #步长初值
beta1=1 #β值
rho=0.55 #ρ1值
tar=Function(myFunc) #初始化函数
if not (tar.value(x+a*d)<=tar.value(x)+rho*a*dot(turn(tar.grad(x)),d):
a=beta1
while tar.value(x+a*d)>tar.value(x)+rho*a*dot(turn(tar.grad(x)),d)):
a*=rho
Wolfe-Powell搜索:
import numpy as np
from Function import Function #定义法求导工具
from lagb import * #线性代数工具库
#假设d已经给出
a=1 #步长初值
beta1=1 #β值
rho=0.55 #ρ1值
sigma=0.4 #σ值
tar=Function(myFunc) #初始化函数
if not (tar.value(x+a*d)<=tar.value(x)+rho*a*dot(turn(tar.grad(x)),d) and dot(turn(tar.grad(x+a*d)),d)>=sigma*dot(turn(tar.grad(x)),d)):
a=beta1
while tar.value(x+a*d)>tar.value(x)+rho*a*dot(turn(tar.grad(x)),d):
a*=rho
while dot(turn(tar.grad(x+a*d)),d)<sigma*dot(turn(tar.grad(x)),d):
a1=a/rho
da=a1-a
while tar.value(x+(a+da)*d)>tar.value(x)+rho*(a+da)*dot(turn(tar.grad(x)),d):
da*=rho
a+=da
强条件的Wolfe-Powell搜索:
import numpy as np
from Function import Function #定义法求导工具
from lagb import * #线性代数工具库
#假设d已经给出
a=1 #步长初值
beta1=1 #β值
rho=0.55 #ρ1值
sigma=0.4 #σ值
tar=Function(myFunc) #初始化函数
if not (tar.value(x+a*d)<=tar.value(x)+rho*a*dot(turn(tar.grad(x)),d) and np.abs(dot(turn(tar.grad(x+a*d)),d))>=sigma*dot(turn(tar.grad(x)),d)):
a=beta1
while tar.value(x+a*d)>tar.value(x)+rho*a*dot(turn(tar.grad(x)),d) and dot(turn(tar.grad(x+a*d)),d)>-sigma*dot(turn(tar.grad(x)),d):
a*=rho
while dot(turn(tar.grad(x+a*d)),d)<sigma*dot(turn(tar.grad(x)),d):
a1=a/rho
da=a1-a
while tar.value(x+(a+da)*d)>tar.value(x)+rho*(a+da)*dot(turn(tar.grad(x)),d) and dot(turn(tar.grad(x+a*d)),d)>-sigma*dot(turn(tar.grad(x)),d):
da*=rho
a+=da
附录
二次函数步长求法:
对于f ( x ) = 1 2 x T Q x + q T x + c f(x)=\frac{1}{2}x^TQx+q^Tx+cf(x)=21xTQx+qTx+c,