第四章 算法: 基本方法
八种不同的数据集形式:
1、只有一种属性承担了所有工作,其他属性都是无关或冗余属性;
2、所有属性是独立地,均等地对最终结果做出贡献;
3、拥有一个包含多个属性的简单逻辑结构,可由决策树得到;
4、存在一些独立的规则,将实例划分到不同的类
5、不同属性子集具有依赖性
6、不同数值属性间有线性依赖关系,权值问题
7、归类到实例空间具体区域,受控于实例间的距离
8、没有提供类别标签,无监督学习
4.1 推断基本规则
- 1规则(1-rule,1 R)选择单个属性作为决策依据,并且选择其中工作性能最好的那个属性;

- 缺失值和数值属性,1 R适用于缺失值和数值属性,在决策树选断点用到类似思想;
4.2 统计建模
概率模型,朴素贝叶斯
- 当训练数据中,类 C i C_iCi 对应的 A j A_jAj 属性取值没有v,那么当一个实例的A j = v A_j=vAj=v,则它属于C i C_iCi的概率为0,因为其他概率将和这个概率相乘,所以最后的结果为0,不是好现象。
- 使用拉普拉斯估计器:

在一个训练实例中,如果一个属性值确实,他就不被包含在频率计数中。
用于文档分类的朴素贝叶斯,多项式朴素贝叶斯(multinomialNaive Bayes)
4.3 分治法:建立决策树
- 基于分治法,自上而下,在每个阶段寻找一个能够将实例按类别分隔的最佳属性;
- 对分隔得到的子问题进行递归处理;
- 信息熵,信息增益,预剪枝,后剪枝;
4.4 覆盖算法:建立规则
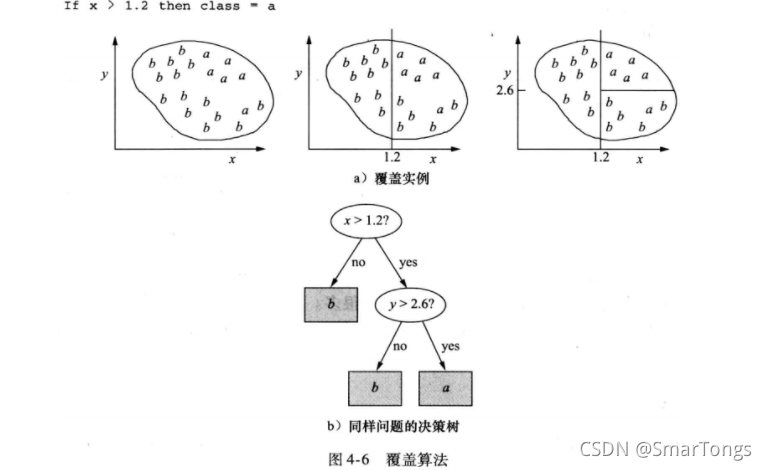
- 规则和树在表达的明晰度上存在差异;
- 规则可以是对称的,树必须首先选择一个属性进行分裂,导致树比等效的规则集大很多;
- 决策树分裂 考虑所有类别的情况,使纯度最大化,生成规则一次只集中处理一个类别;
4.5 挖掘关联规则
4.6 线性模型
- 数值预测:线性回归;
- 线性分类:Logistic回归;多响应线性回归(multi-response linear regression)
4.7 基于实例的学习
距离函数
规范化:

缺失值处理:
- 对于名目属性:假设缺失属性与其他属性的差值达到最大值。当且仅当两个属性非缺失且相同时距离为0;
- 对于数值属性:两个缺失值只差也是1,如果仅有一个属性缺失,差是另一个属性的规范值,或者是max(1-v,v)。
有效寻找最近邻:
- 单独预测花费的时间与训练实例的数量成比例关系,尤其是对于大数据量,高维属性;
- 以树的形式表示训练实例,更加有效的寻找最近邻实例,kD-tree;
**k-D树(k-dimensional)**是一个二叉树,用超平面分割实例空间,每个部分递归分裂。主要应用于多维空间关键数据的搜索(如:范围搜索和最近邻搜索)。
树的建立,建立的树应当尽量平衡:
定义节点的数据结构:每个节点的域:
Node-data-数据向量,实例,n维向量;
Range-空间矢量,该节点代表的空间范围;
split-int,选择哪个维度进行划分;
Left-k-d-tree、Right-k-d-tree;
parent-k-d-tree父节点;选取轴点,对于待划分的所有子数据,统计它们在每个维度的方差,选出最大方差对应的维,就是split域的值。子数据按照split维升序排序,取中间点作为轴点。
邻近搜索,给定一个KD-Tree和一个节点,求KD-Tree中距离这个节点最近的节点
距离公式用欧式距离:
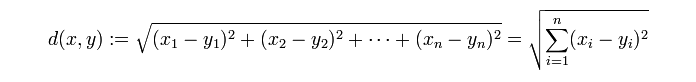
首先通过二叉树搜索,比较待查找节点和分裂节点在split维上的值,小于等于进入左子树,大于进入右子树,同时记录搜索路径。沿着搜索路径,很快找到最近邻的近似点,及与待查点处于同一个子空间的叶子节点。回溯搜索路径(用到队列),判断搜索路径上节点的其他子空间中有无距离查询点更近的数据点,如果有,跳到其他子节点空间中搜索,直到搜索路径为空。
在判断其他子节点空间中是否有可能有距离查询点更近的数据点时,做法是以查询点为圆心,以当前的最近距离为半径画圆,这个圆称为候选超球candidate hypersphere,如果圆与回溯点的轴相交,则需要将轴另一边的节点都放到回溯队列里面来。
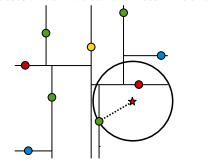
举例
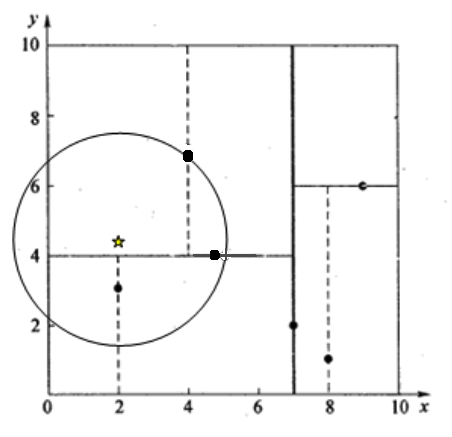
我们来查找点(2,4.5),在(7,2)处测试到达(5,4),在(5,4)处测试到达(4,7),然后search_path中的结点为<(7,2), (5,4), (4,7)>;
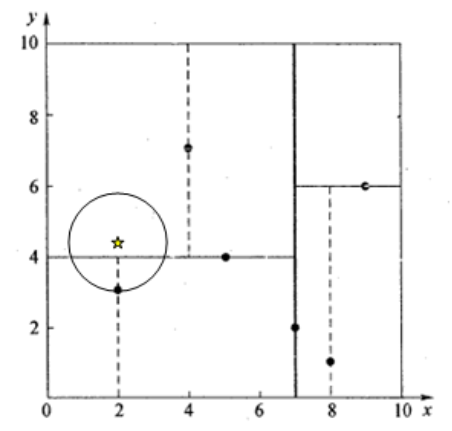
从search_path中取出(4,7)作为当前最佳结点nearest, dist为3.202;然后回溯至(5,4),以(2,4.5)为圆心,以dist=3.202为半径画一个圆与超平面y=4相交,如下图,所以需要跳到(5,4)的左子空间去搜索。**所以要将(2,3)加入到search_path中,现在search_path中的结点为<(7,2), (2, 3)>;**另外,(5,4)与(2,4.5)的距离为3.04 < dist = 3.202,所以将(5,4)赋给nearest,并且dist=3.04。回溯至(2,3),(2,3)是叶子节点,直接判断(2,3)是否离(2,4.5)更近,计算得到距离为1.5,所以nearest更新为(2,3),dist更新为(1.5)回溯至(7,2);
同理,以(2,4.5)为圆心,以dist=1.5为半径画一个圆并不和超平面x=7相交, 所以不用跳到结点(7,2)的右子空间去搜索。至此,search_path为空,结束整个搜索,返回nearest(2,3)作为(2,4.5)的最近邻点,最近距离为1.5。
4.8 聚类
基于距离的聚类,经典的k均值(k-means),只是类内样本到类中心距离平方和的局部最小值,对初始点的选取较为敏感。经常是随机多选几次初始点,选择结果最好的。
k-means++:为k-means算法选取初始种子的算法。它是NP-hard k-means问题的一种近似算法,它是一种避免标准k-means算法有时发现较弱聚类的方法,可以很快收敛;
假设已经选取了n个初始聚类中心(0<n<K),则在选取第n+1个聚类中心时:距离当前n个聚类中心越远的点会有更高的概率被选为第n+1个聚类中心。在选取第一个聚类中心(n=1)时同样通过随机的方法。
算法步骤:

elkan K-Means 优化距离计算
- 目标:减少不必要的距离的计算
- 规则:对于样本点x xx,两个质心u j 1 , u j 2 u_{j1},u_{j2}uj1,uj2,如果我们预先计算了两个质心之间的距离D ( j 1 , j 2 ) D(j_1,j_2)D(j1,j2),同时,计算发现2 D ( x , j 1 ) ≤ D ( j 1 , j 2 ) 2D(x,j_1) \leq D(j_1,j_2)2D(x,j1)≤D(j1,j2),则推出D ( x , j 1 ) ≤ D ( x , j 2 ) D(x,j_1)\leq D(x,j_2)D(x,j1)≤D(x,j2)。此时不再需要计算D ( x , j 2 ) D(x,j_2)D(x,j2)。
Mini Batch K-Means 优化大样本计算
- 用样本集中的一部分的样本来做传统的K-Means,加快收敛。同时保证聚类精确度降幅在可接受的范围之内。
- 选择合适的批样本大小batch size,仅用batch size个样本来做K-Means聚类。这batch size个样本一般通过无放回的随机采样得到的。为了增加算法的准确性,我们一般会多跑几次Mini Batch K-Means算法,用得到不同的随机采样集来得到聚类簇,选择其中最优的聚类簇。
常见优化方法:

4.9 多实例学习
- 数据里的每一个样本都是由多个不同实例组成,我们将这些样本称之为袋bag。在有监督的多实例学习中,一个类的类标号和每一个bag相关。
- 可以通过计算平均值、众数、最小值、最大值等来概括描述袋中实例并将这些值添加为新属性,将多实例问题转化为单实例问题。训练数据bag包含的实体数量不同,赋予某袋中每个实例反比于bag大小的权重。如果一个bag包含n个实例,那么赋予其中每个实例1/n的权重