多维随机变量及其分布

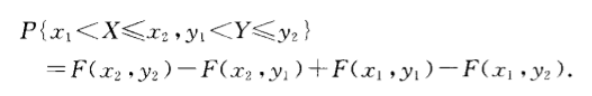
• 边缘分布函数:
  $$\begin{gathered} F_X(x)=P\{X\le x\}=P\{X\le x,Y<\infty \}=F(x,\infty ) \\ {F}_Y(y)=F(\infty ,y) \end{gathered}$$
• 边缘概率密度:
  $$\begin{gathered} f_X(x)={\int }_{-\infty }^{\infty }f(x,y)dy \\ {f}_Y(y)={\int }_{-\infty }^{\infty }f(x,y)dx \end{gathered}$$

条件分布

• 条件概率密度:
  
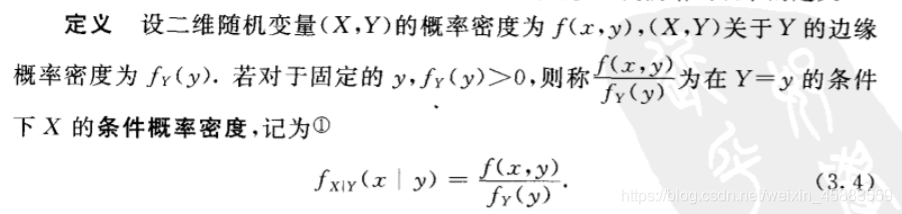
• 条件分布函数:
  
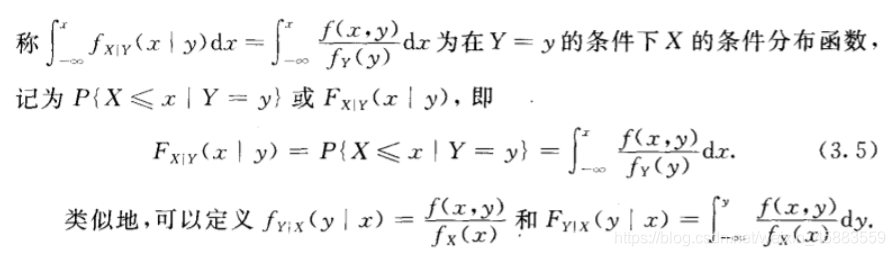
• 均匀分布:
  
• 相互独立:
  

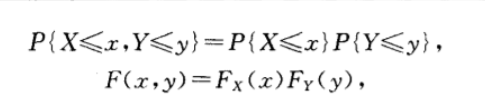
称随机变量X和Y相互独立.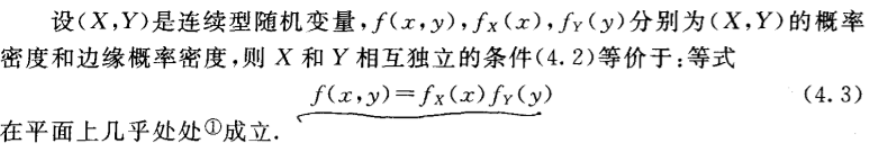



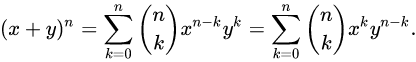
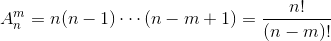
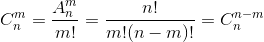=h(z,y)

两个随机变量的函数的分布

• 设$f(x,y),z=g(x,y),x=h(y,z)$
  $$f_Z(z)={\int }_{-\infty }^{\infty }f(h(y,z),y)|\frac{\partial h(y,z)}{\partial z}|dy$$

• Z=X+Y
  

• Z=Y/X, Z = XY:
  

• M = max{X,Y}, N = min{X,Y}
  
  设X,Y为相互独立的变量, 他们都服从正态分布$N(0,{\sigma }^2)$,则$Z=\sqrt{X^2+Y^2}$的概率密度为
  $$f_z(z)=\{\begin{array}{l}\frac{z}{{\sigma }^2}{e}^{-z^2/(2{\sigma }^2)},z\ge 0\\ 0,其他\end{array}$$