python 旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。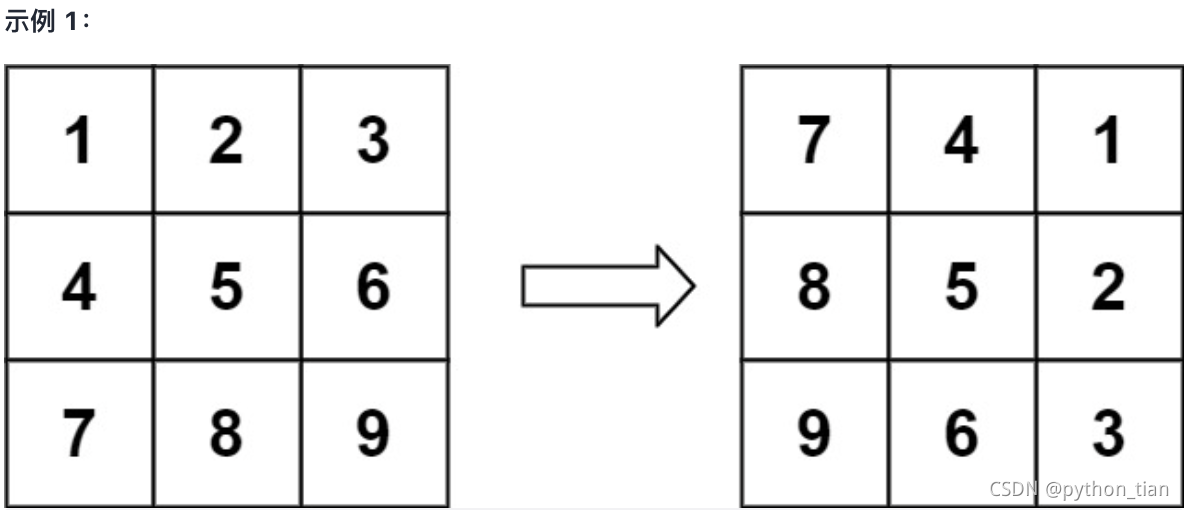

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]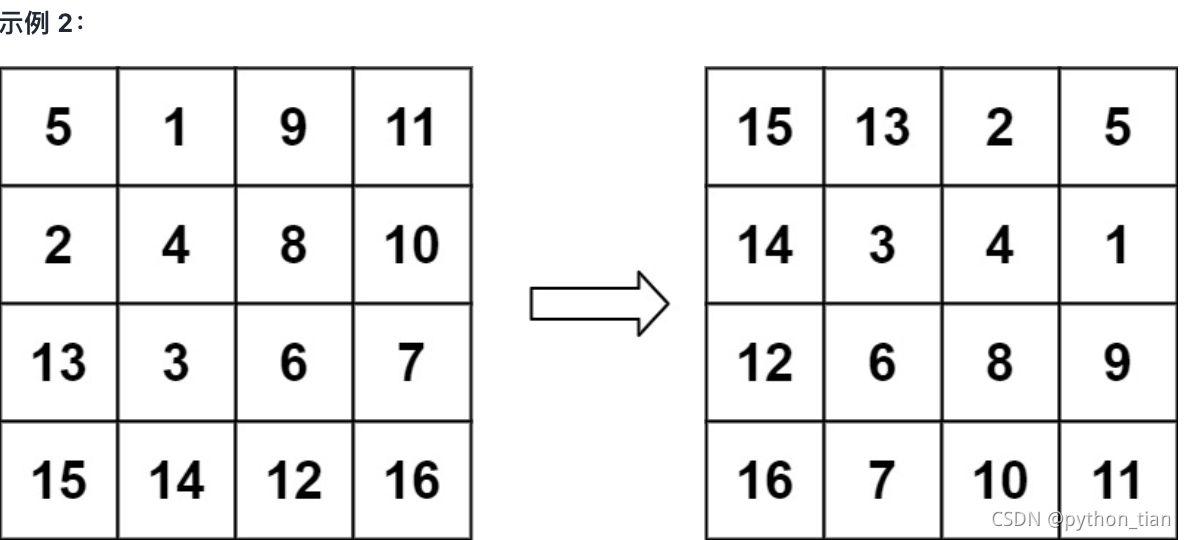

输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
示例 3：

输入：matrix = [[1]]
输出：[[1]]
示例 4：

输入：matrix = [[1,2],[3,4]]
输出：[[3,1],[4,2]]

提供三种解题思路

1. 借助辅助数组,循环替换数据

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        # 解题思路一
        # 借助辅助数组，循环替换数据

        import copy
        copy_matrix = copy.deepcopy(matrix)

        n = len(matrix)
        if n == 1:
            return matrix
        for i in range(n):
            for j in range(n):
                matrix[i][j] = copy_matrix[n-j-1][i]
        return matrix

2. 两次翻转达到旋转的效果—>先沿左右中线翻转(上下翻转), 再沿-45度对角线翻转

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        # 解题思路二
        # 两次翻转解题 先沿左右中线翻转(上下翻转)，再沿-45度对角线翻转
        length = len(matrix)
        for j in range(length):
            for i in range(length//2):
                matrix[j][i], matrix[j][length-i-1] = matrix[j][length-i-1], matrix[j][i]
        
        n = length - 1
        m = n
        for j in range(n):
            for i in range(m):
                matrix[j][i], matrix[n-i][n-j] = matrix[n-i][n-j], matrix[j][i]
            m -= 1
        return matrix

3.标准的原地旋转

解题思路是: 以左上，右上，右下， 左下 四个顶点为起始点， 分别向右旋转，四个位置相互交换，交换结束后，左上横坐标加1，右上纵坐标加1，右下横坐标减1，左下纵坐标减1，依次类推，把最外层的数据全部旋转。
接着跳转到内圈，还是上边的旋转逻辑，直到旋转结束。

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        # 解题思路三
        # 标准的原地翻转
        n = len(matrix)
        d_i, d_j, x = 0, 0, 0
        for j in range(d_j, n-d_j-1):
            for i in range(d_i, n-d_i-1):
                temp_val = matrix[j][i]
                matrix[j][i] = matrix[n - i - 1][j]
                matrix[n - i - 1][j] = matrix[n - j - 1][n - i - 1]
                matrix[n - j - 1][n - i - 1] = matrix[i][n - j - 1]
                matrix[i][n - j - 1] = temp_val
                d_i += 1
            d_j += 1
            x += 1
            d_i = x
        return matrix