神经网络预测模型算法_如何建立神经网络预测模型

最近忙毕设,公众号好久没更新，想来想去不知道写啥，就讲点毕设里面用到的神经网络预测模型吧！
模型平台：MATLAB

1 模型输入输出介绍

1.1 回归神经网络模型输入输出介绍

输入神经元可以理解为自变量，输出神经元可理解为因变量。
如果用矩阵表示输入输出的话，每一行矩阵表示一个神元，每一列表示一组数据，这里由于输入输出数据量较大可以采用第三方数据库导入数据的方式，部分情况下由于导入数据神经元是列向量形式，导入后需要进行转置。

% 输入数据矩阵，并将导入的结构数组转换成矩阵
u = cell2mat(struct2cell(load('data.mat'))); %导入mat文件数据
p = u(1:5,:);                                %1-5行表示5个输入神经元
t = u(6:7,:);                                %6-7行表示2个输出神经元

% 导入数据Excel数据
ta = xlsread('data.xlsx', 'sheet1', A1:E366')';%数据读入
u = ta';        %ta每列表示神经元，输入模型需转置成每行表示
p = u(1:4,:);   %1-4行表示4个输入神经元
t = u(   5,:);  %  5行表示1个输出神经元

1.2 时序神经网络模型输入输出介绍

输入输出神经元为一系列时序数据，前后数据相关性强，可以用前面的数据预测后面的数据。
数据导入方式同上，下面显示时序模型输入输出的转换形式，具体为用前 30 个数据预测后 30 个数据。

%导入365个数据
data= xlsread('data.xlsx', 'sheet1', 'A1:A365');
lag = 30;                  %利用前30天数据做为输入，去预测下30天数据
n = length(data);          %计算数据长度
u = 365-lag*2+1;
%准备输入和输出数据
p = zeros(lag,u);
for  i = 1:u
     p(:,i) = data(i:i+lag-1);       %数据赋值
end
     t = zeros(lag,u);
for  i = 1:u
     t(:,i) = data(i+lag:i+2*lag-1); %数据赋值
end

举一反三，利用前 5 个数据预测后五个输入输出数据的确定

%利用前5天数据做为输入，去预测下5天数据，其他源码同上
data= xlsread('data.xlsx', 'sheet1', 'A1:A365')';
lag = 5;

2 BP 神经模型搭建

2.1 模型数据预处理

数据划分
训练集——模型建立的数据，相当于拟合函数的参数的数据
有效集——确定网络结构或者控制模型复杂程度的参数，这里笔者通过查看大量源码，神经网络预测模型中部分参数是确定的，因而不需划分有效集，有建议的伙伴可一起探讨！
测试集——主要测试训练好的模型的预测能力
数据标准化函数 mapminmax 和 premnmx
先将数据归一化输入模型训练，之后反归一化输出结果，常用的函数为 mapminmax。

%mapminmax归一化用法
[inputn,inputps]  = mapminmax(input_train);
[outputn,outputps]= mapminmax(output_train);
%premnmx归一化用法
[SIn, minp, maxp, SOut, mint, maxt] =premnmx(input_train, output_train))

2.2 网络参数和函数的选择

传输函数的选择
常见的传输函数的类型有 3 种(purelin，logsig，tansig)，如图 2-1 所示，设定 TF1 为神经网络的隐藏层的传输函数，设定 TF2 为神经网络的输出层的传输函数。隐藏层的传输函数三者皆用，常用 tansig 函数；输出层传输函数用 purelin 和 logsig，常用 purelin。

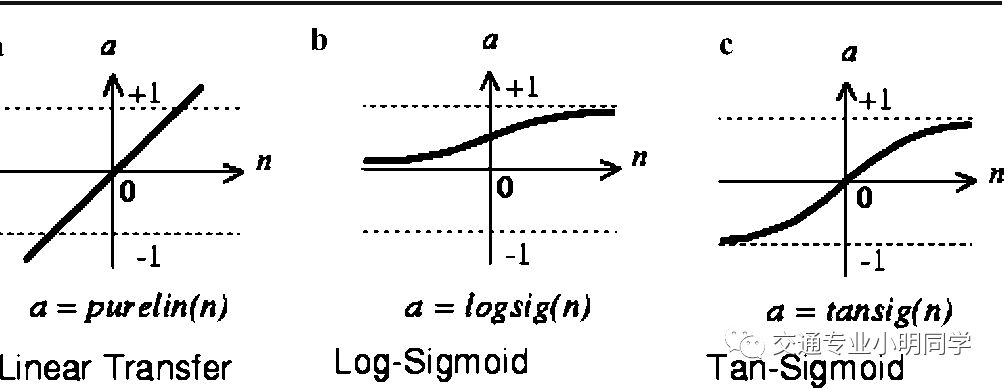
网络参数的设置
net.trainParam.epochs 设置训练次数；
net.trainParam.goal 设置训练目标，适宜为主；
net.trainParam.lr 设置学习率，应设置为较少值，太大虽然会在开始加快收敛速度，但临近最佳点时，会产生动荡，而致使无法收敛；net.trainParam.mc 设置动量因子的，默认为 0.9；
net.trainParam.show 显示的间隔次数。
BP 网络的创建
net=newff(p,t,[10,2],{TF1 TF2},'traingdm')；p,t 为数据集，[10,1]表示网络含两个隐藏层，{TF1 TF2}表示传输函数，'traingdm'表示训练算法，下面讲到具体算法选择，可指定具体算法训练。
网络算法的选取
net.trainFcn 指定训练算法
大型网络的首选算法——
'trainrp'表示 RPROP(弹性 BP)算法,内存需求最小。
'traincgf'表示 Fletcher-Reeves 修正算法；
'traincgp'表示 Polak- Ribiere 修正算法，内需比 Fletcher-Reeves 修正略大；'traincgb'表示 Powell-Beal 复位算法，内存需求比 Polak-Ribiere 修正算法略大，3者皆为共轭梯度算法。
'trainscg'表示 ScaledConjugate Gradient 算法,与 Fletcher-Reeves 修正相同,计算量比上面三种算法都小；
'trainbfg'表示 Quasi-Newton Algorithms - BFGS Algorithm,计算量和内存需求均比共轭梯度算法大,但收敛比较快；
'trainoss'表示 OneStep Secant Algorithm,计算量和内存需求均比 BFGS 算法小,比共轭梯度算法略大。
中型网络的首选算法——
'traingd'表示梯度下降算法；
'traingdm'表示动量梯度下降算法；
'traingda'表示变学习率梯度下降算法；
'traingdx'表示变学习率动量梯度下降算法；
'trainlm'表示 Levenberg-Marquardt 算法,内存需求最大,收敛最快；
'trainbr'表示贝叶斯正则化算法；
'trainscg'表示 ScaledConjugate Gradient 算法；
'trainrp'表示 RPROP(弹性 BP)算法；
'trainscg'表示 ScaledConjugate Gradient 算法；
'trainoss'表示 OneStep Secant Algorithm。
常见的有代表性的五种为'traingdx','trainrp','trainscg','trainoss', 'trainlm'，在这里一般是选取'trainlm'函数来训练，其算对对应的是 Levenberg-Marquardt 算法。

net.trainParam.epochs = 5000;
net.trainParam.lr = 0.05;
net.trainParam.goal = 1e-5;
net=newff(inputn,outputn,[30 30],{TF1 TF2},'trainlm');

2.3 模型测试数据预测输出

回归模型测试数据预测

%% BP网络预测
%预测数据归一化
inputn_test = mapminmax('apply',input_test,inputps);
%网络预测输出
an = sim(net,inputn_test);
%网络输出反归一化
BPoutput = mapminmax('reverse',an,outputps);

时序模型测试数据预测

%% BP网络数据拟合
%预测数据归一化
input_test = input_train;
inputn_test= mapminmax('apply',input_test,inputps);
%网络预测输出
an = sim(net,inputn_test);
%网络输出反归一化
BPoutput = mapminmax('reverse',an,outputps);%30*306
o1 = BPoutput(1,1:end-1);            %第一行除去最后一个数
o2 = BPoutput(:,end)';               %最后一列转置
BPoutputnew = [o1 o2];%合并,31-365,335预测数据
output_test = data(31:365)';%335数据
%提取后92预测数据(拓展)
BPoutputnewplus = BPoutputnew(244:335);%244-335,92预测数据
output_testplus = data(274:365)';      %92实际数据
ccc = BPoutputnewplus';
xlswrite('C1.xlsx',ccc, 'sheet2', 'B1:B92');
%% 未来30天预测
%输入单组数据进行网络测试
aftest = data(336:365);
aftestn= mapminmax('apply',aftest,inputps);
%网络预测输出
af = sim(net,aftestn);
%网络输出反归一化
afoutput = mapminmax('reverse',af,outputps);
aaf = afoutput';
afBPoutputnew = [o1 o2 aaf];%合并,31-395,365数据

3 数据可视化分析

3.1 输出数据分析

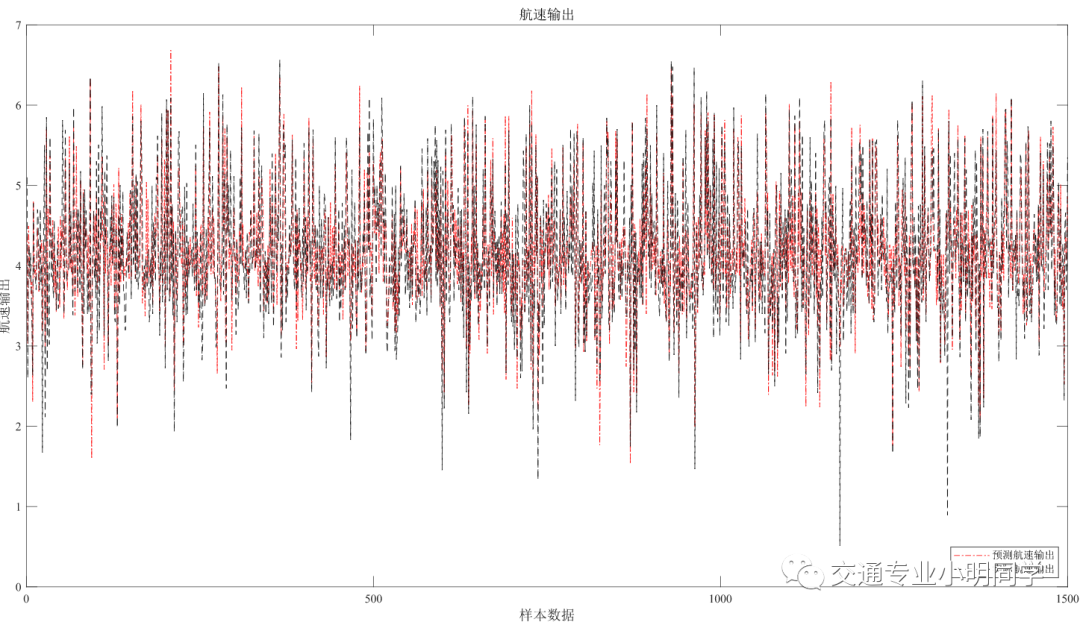
回归模型实际数据与预测数据曲线绘图——以二元输出为例

%航速
figure(1)
plot(BPoutput(1,:),'r-.')
hold on
plot(output_test(1,:),'k--');
set(gca, 'Fontname', 'Times New Roman','FontSize',10);
legend('预测航速输出','实际航速输出','Location','SouthEast','FontName','宋体')
title('航速输出','fontsize',12,'FontName','宋体')
ylabel('航速输出','fontsize',12,'FontName','宋体')
xlabel('样本数据','fontsize',12,'FontName','宋体')
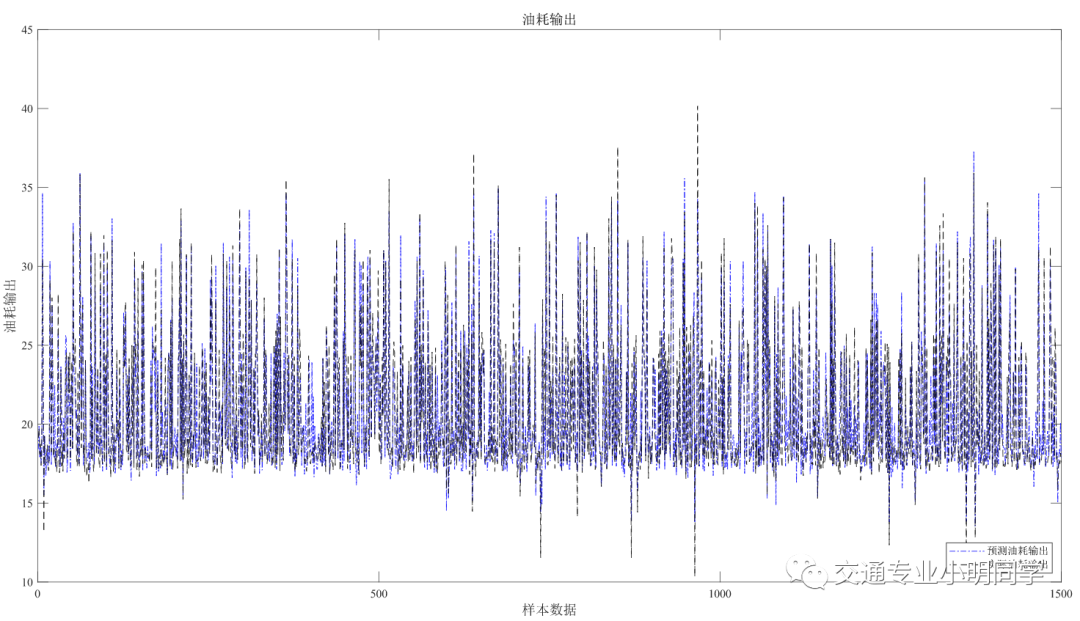
%油耗
figure(2)
plot(BPoutput(2,:),'b-.')
hold on
plot(output_test(2,:),'k--');
set(gca, 'Fontname', 'Times New Roman','FontSize',10);
legend('预测油耗输出','实际油耗输出','Location','SouthEast','FontName','宋体')
title('油耗输出','fontsize',12,'FontName','宋体')
ylabel('油耗输出','fontsize',12,'FontName','宋体')
xlabel('样本数据','fontsize',12,'FontName','宋体')

时序模型实际数据与预测数据曲线绘图——以 365 个数据预测为例

num1 = 31:395;
num2 =  1:365;
figure;
plot(num1 ,afBPoutputnew,'g-.',num2,data(1:end),'--+')
set(gca, 'Fontname', 'Times New Roman','FontSize',10);
legend('预测数据','实际数据','Location','NorthWest','FontName','宋体');
xlabel('时间','fontsize',12,'FontName','宋体');
ylabel('数值','fontsize',12,'FontName','宋体');

3.2 误差数据分析

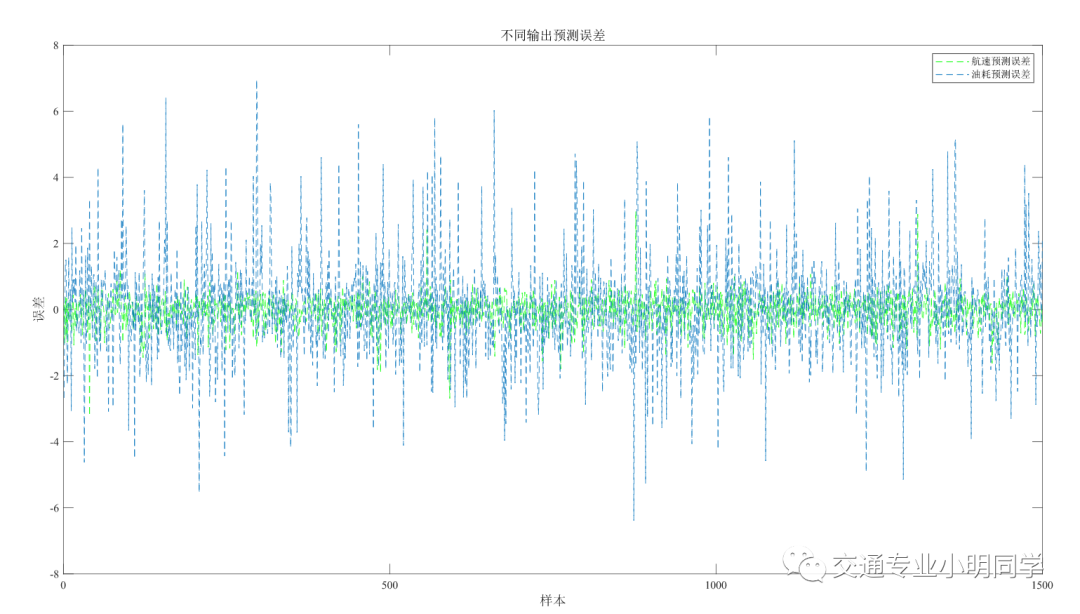
误差可视化分析

%预测误差
error1 = BPoutput(1,:)-output_test(1, :);
error2 = BPoutput(2,:)-output_test(2, :);
errors = [error1 error2 ];
figure
plot(error1,'--')
hold on
plot(error2,'y--')
set(gca, 'Fontname', 'Times New Roman','FontSize',10);
legend('航速预测误差','油耗预测误差','Location','NorthEast','FontName','宋体')
title('不同输出预测误差','fontsize',12,'FontName','宋体')
ylabel('误差','fontsize',12,'FontName','宋体')
xlabel('样本','fontsize',12,'FontName','宋体')

拓展分析

%预测误差百分比
errp1 = (output_test(1,:)-BPoutput(1,:))./BPoutput(1,:);
errp2 = (output_test(2,:)-BPoutput(2,:))./BPoutput(2,:);
%模型检验
A = output_test;
H = BPoutputnew;
epsilon = A - H;                                         %计算残差序列
%残差Q检验
absepsilon = abs(epsilon);                 %计算相对误差序列
%计算相对误差序列
delta = abs(epsilon./A);                   %计算平均相对误差Q
Q = mean(delta);
%% 方差比C检验
S1 = std(A, 1);
S2 = std(epsilon, 1);
C  = std(epsilon, 1)/std(A, 1);
%% 小误差概率P检验
tmp = find(abs(epsilon - mean(epsilon))< 0.6745 * S1);
disp('小误差概率P检验：')
P = length(tmp)/n
%% 关联度r检验
mn = min(min(absepsilon'));
mx = max(max(absepsilon'));
rho = 0.5;
ksi = (mn+rho*mx)./(absepsilon+rho*mx);
r = sum(ksi')/n;
figure
plot(r,'r--');
legend('关联度','Location','NorthEast','FontName','宋体')
title('数据关联度','FontName','宋体')
ylabel('关联度','fontsize',12,'FontName','宋体')
xlabel('样本','fontsize',12,'FontName','宋体')

好了，这次分享就到这了，撰文不易，喜欢的话可以分享一下哦!

主要参考博客：https://blog.csdn.net/y1535766478/article/details/79607165

原文链接：https://blog.csdn.net/weixin_33365214/article/details/113453453