
本篇介绍灰度直方图和均衡化,也是属于图像灰度变换得范畴;
一、直方图
直方图:表示图像中具有某种灰度级的像素的个数,反映了图像中每种灰度出现的频率。是图像最基本的统计特征。
横坐标:灰度级;
纵坐标:该灰度级出现的个数;
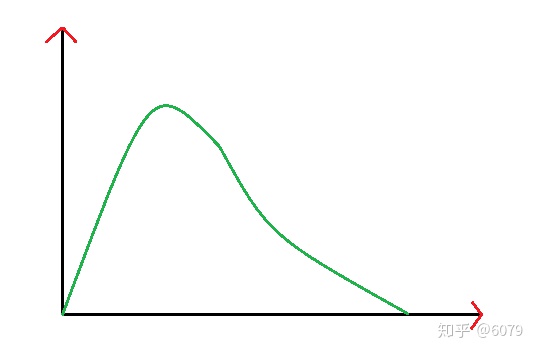
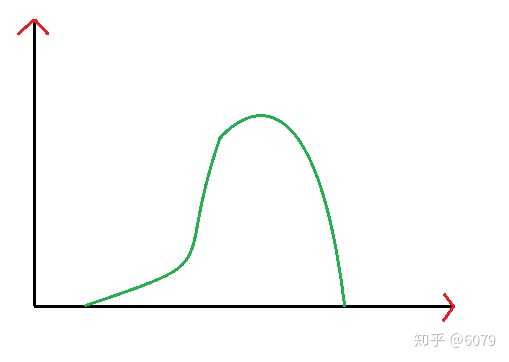
从上面两个直方效果图可以看出:图一比较暗,图二比较亮;
直方图性质:
1、直方图只代表图片中灰度值出现的次数(频率),看不出灰度图的位置,位置信息丢失;
2、一个图像只有一个直方图,但是一个直方图可以对应多张图像;
3、可以把一张图片分成几个直方图,然后把这几个直方图求和,会得到一张图片的直方图;
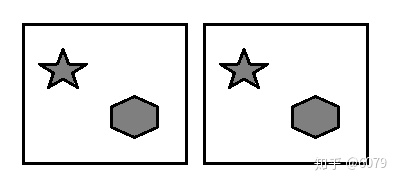
1、图像直方图多对一:上图两张图片是两张不同的图片,但是五角星和六边形的位置不同,但是他们的直方图肯定是一样的;
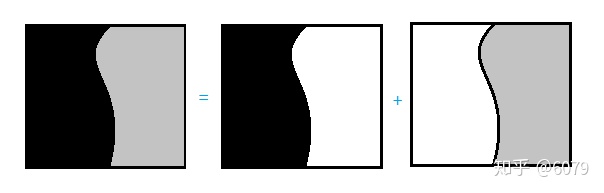
二、图像分解:下图对一张图分解,一张图片的直方图等会几个直方图之和;
直方图计算:
因为图像处理已经是离散化的数值了,所以在离散的情况下,Rk代表灰度级数,我们把灰度级数归一化(灰度级数归一化:灰度级数除以255就得到了归一化数值)
如下图:rk代表离散灰度级,nk为图像中出现Rk级灰度的像素数,n是图像像素总数,nk/n即为频数,最后就可以求得直方图的数值了。;
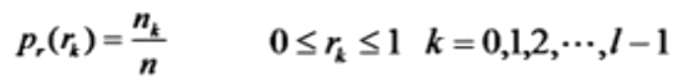
直方图计算:
1、初始化数组,
2、统计灰度图的个数;
3、归一化
二、灰度直方图的均衡化
对原图直方图进行均衡化之后,虽然不是很平坦,但是比原图直方图平坦(每个颜色出现的次数相等)的多;扩展了动态范围,以前很窄,现在把其拉开;对于对比度出现很暗或者很亮的地方,没有什么对比度或集中在一块;通过均衡化一下就能把图像给拉开;
均衡化的特点:变换之后的级数(原来是256级,均衡化之后就小于256)变少,叫简并现象;灰度级数变少,并不一定会影响视觉感官,反之提高了视觉接受力;
均衡化计算:
利用累计分布函数作为灰度变换函数;
举例:
假如一张图片有八种颜色,每种颜色出现的概率就是直方图;用累积法,累积概率密度:当前的直方图概率和前面累加;对于每一个累积乘以最大的灰度值,加0.5取整,就得到转变后的颜色:原来为0的像素变为1,2变为1,3变为2以此类推;均衡化之后,有的灰度就没了;最后就得到了一种映射关系,原来什么值,均衡化之后改为什么值;
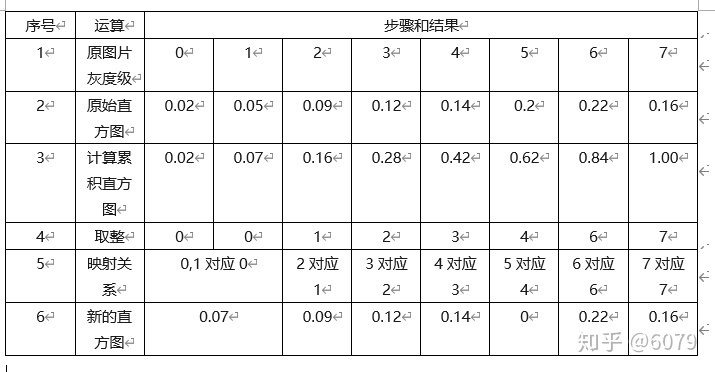
总结:
1、统计直方图数组,用一个数组HistogramUntreadImageArray记录HistogramUntreadImageArray[i]
2、i从1开始,另CumulativehistogramArray[i]= CumulativehistogramArray[i-1] +
HistogramUntreadImageArray[i]
用TempArray数组记录新的CumulativehistogramArray索引值,即:
TempArray[i] = CumulativehistogramArray[i] * (256 - 1)
3、依次循环每一个像素,取原图的像素值作为数组TempArray的下标值,取该下标对应的TempArray数组值为均衡化之后的像素值;
直方图和直方图均衡先暂时到这,下篇文章介绍灰度变换得代码,请耐心等待;
喜欢的话,可以关注,一起学习,一起进步。有错误的请指出;