本文使用 Python 语言,实现一个 Dijkstra 算法的简单算例。
有关算例及算法流程,见博客:
Dijkstra 算法流程的举例说明

代码实现:
from datetime import datetime
from typing import List, Tuple
def dijkstra(mat_distance: List[List[int]], start: int, m: int = 10 ** 8) -> Tuple[List[int], List[int]]:
"""
Dijkstra algorithm
:param mat_distance: distance matrix
:param start: start point
:param m: big m
:return: list_distance: list of distance from start point to other nodes
"""
# number of nodes
num_node = len(mat_distance)
# result data: distance list
list_distance = [m for _ in range(num_node)]
list_node_from = [0] + [-1 for _ in range(num_node - 1)]
# intermediate data
# if node status is optimal
list_if_opt = [False for _ in range(num_node)]
# if edge checked
mat_distance_check = [[False for _ in range(num_node)] for _ in range(num_node)]
# nearest node from start point
list_distance_start = [d if d > 0 else m for d in mat_distance[start]]
nearest_start = list_distance_start.index(min(list_distance_start))
print("nearest node from start point: {}".format(nearest_start), '\n')
node = start
list_distance[start] = 0
list_if_opt[start] = True
list_next_node = [start] # start node list, current node to search forward
while False in list_if_opt:
# from current node on
for i in range(num_node):
# if next node can reach and not optimal
if not list_if_opt[i] and mat_distance[node][i] >= 0:
if list_distance[node] + mat_distance[node][i] < list_distance[i]:
list_distance[i] = list_distance[node] + mat_distance[node][i]
list_node_from[i] = node
mat_distance_check[node][i] = True
print("get node {}, edge distance {}, distance list update to {}".format(
i, mat_distance[node][i], list_distance[i]))
# update next node optimal status
if i == nearest_start:
if_opt = True
else:
if_opt = True
for j in range(num_node):
if mat_distance[j][i] >= 0:
if not (list_if_opt[j] and mat_distance_check[j][i]):
if_opt = False
break
print("next node {} optimal: {}".format(i, if_opt))
if if_opt:
list_if_opt[i] = True
list_next_node.append(i) # if optimal, add to start node list
list_next_node.remove(node) # forward finish, remove current node from start node list
node = list_next_node[0] # set start node list's 1st node as current node
print()
return list_distance, list_node_from
if __name__ == '__main__':
mat_distance_ = [[-1, 100, 30, -1, -1],
[-1, -1, 20, -1, -1],
[-1, -1, -1, 10, 60],
[-1, 15, -1, -1, 50],
[-1, -1, -1, -1, -1]]
start_ = 0
print()
dts = datetime.now()
list_distance_, list_node_from_ = dijkstra(mat_distance=mat_distance_, start=start_)
dte = datetime.now()
tm = round((dte - dts).seconds + (dte - dts).microseconds / (10 ** 6), 3)
print("Dijkstra algorithm running time: {} s".format(tm), '\n')
print("result distance list: {}".format(list_distance_))
print("optimal distance node from: {}".format(list_node_from_), '\n')
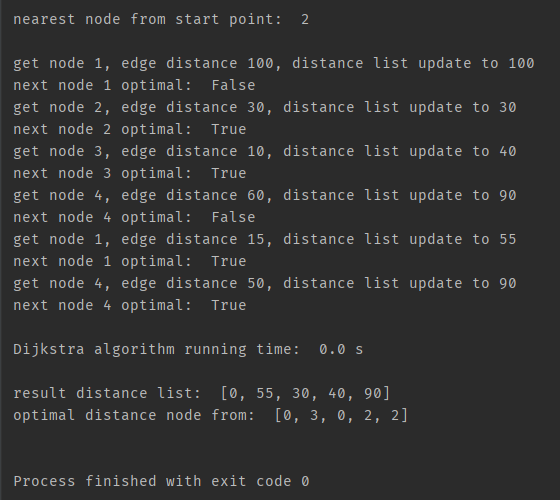
运行效果:
版权声明:本文为Zhang_0702_China原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。