【回溯算法】旅行商问题--TSP问题

【问题描述】

一销售商从n个城市中的某一城市出发，不重复地走完其余n—1个城市并回到原出发点，在所有可能的路径中求出路径长度最短的一条。本题假定该旅行商从第1个城市出发。

输入

对每个测试例，第1行有两个整数：n(4≤n≤10)和m(4≤m≤20 ) ，n是结点数，m是边数。

接下来m行，描述边的关系，每行3个整数：(i，j)，length，表示结点i到结点j的长度是length。

当n＝0时，表示输入结束。

输出

对每个测试例，输出最短路径长度所经历的结点，最短的长度。

输入样例

4 6

1 2 20

1 4 4

1 3 6

2 3 5

2 4 10

3 4 15

0

输出样例

1 3 2 4

25

【算法分析】

旅行商问题的解空间是一棵排列树。 开始时，x＝｛1，2，…，n｝，相应的排列树由x的全排列构成。

TSP问题(Traveling Salesman Problem)通常称为旅行商问题，也称为旅行售货员问题、货担郎问题等，是组合优化中的著名难题，也是计算复杂性理论、图论、运筹学、最优化理论等领域中的一个经典问题，具有广泛的应用背景。

问题的一般描述为：旅行商从n个城市中的某一城市出发，经过每个城市仅有一次，最后回到原出发点，在所有可能的路径中求出路径长度最短的一条。

设G=(V, E)是一个带权图，其每一条边(u, v)∈E的费用（权）为正数w(u, v)。目的是要找出G的一条经过每个顶点一次且仅经过一次的回路，即汉密尔顿（Hamilton）回路v1，v2 ，…，vn ，使回路的总权值最小：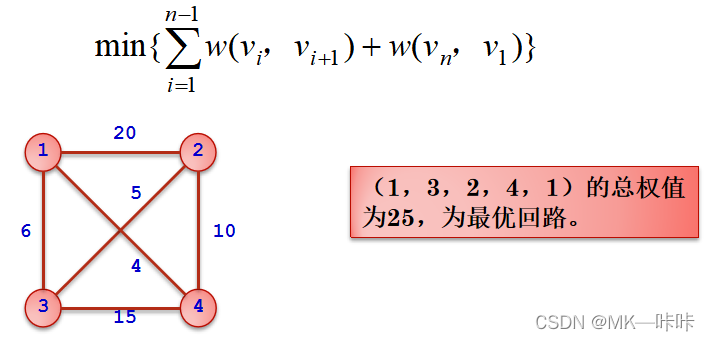

【代码部分】 

//旅行商问题回溯算法的数据结构

#define NUM 100
int n;				//图G的顶点数量
int m;				//图G的边数
int a[NUM][NUM];		//图G的邻接矩阵
int x[NUM];			//当前解
int bestx[NUM];		//当前最优解向量
int cc;				//当前费用
int bestc;			//当前最优值
int NoEdge = -1;		//无边标记

//在构造邻接矩阵a时，其初始值应为NoEdge：
for (i=0; i<NUM; i++)
　　for (j=1; j<NUM; j++)
　　　　a[i][j] = NoEdge;

//最优值和向量x的初始化数值如下：
bestc = NoEdge;
for(i=1; i<=n; i++)
　　x[i] = i;

//旅行商问题回溯算法的实现
//形参t是回溯的深度，从2开始
void Backtrack(int t)
{
　　//到达叶子结点的父结点
　　if(t==n)
　　{
　　　　if(a[x[n-1]][x[n]]!= NoEdge && a[x[n]][1]!= NoEdge && 
　　　　　　(cc + a[x[n-1]][x[n]]+a[x[n]][1]<bestc||bestc== NoEdge))
　　　　{
　　　　　　for(int i=1; i<=n; i++)
　　　　　　　　bestx[i] = x[i];
　　　　　　bestc = cc + a[x[n-1]][x[n]] + a[x[n]][1];
　　　　}
　　　　return;
　　}
else 
　　{
　　　　for(int i=t; i<=n; i++)
　　　　{
　　　　　　if(a[x[t-1]][x[i]]!= NoEdge &&
　　　　　　　　(cc + a[x[t-1]][x[i]]< bestc||bestc == NoEdge))
　　　　　　{
　　　　　　　　swap(x[t],x[i]);
　　　　　　　　cc += a[x[t-1]][x[t]];
　　　　　　　　Backtrack(t+1);
　　　　　　　　cc -= a[x[t-1]][x[t]];
　　　　　　　　swap(x[t],x[i]);
　　　　　　}
　　　　}
　　}
}

//完整实现
#include <iostream>
using namespace std;

#define NUM 100
int n;
int m;
int a[NUM][NUM];
int x[NUM];
int bestx[NUM];
int cc;
int bestc;
int NoEdge = -1;

void Backtrack(int t)
{
	if(t==n)
	{
		if(a[x[n-1]][x[n]]!= NoEdge && a[x[n]][1]!= NoEdge && 
			(cc + a[x[n-1]][x[n]]+a[x[n]][1]<bestc||bestc== NoEdge))
		{
			for(int i=1; i<=n; i++)
				bestx[i] = x[i];
			bestc = cc + a[x[n-1]][x[n]] + a[x[n]][1];
		}
		return;
	}
	else 
	{
		for(int i=t; i<=n; i++)
		{
			if(a[x[t-1]][x[i]]!= NoEdge &&
				(cc + a[x[t-1]][x[i]]< bestc||bestc == NoEdge)) 
			{
				swap(x[t],x[i]);
				cc += a[x[t-1]][x[t]];
				Backtrack(t+1);
				cc -= a[x[t-1]][x[t]];
				swap(x[t],x[i]);
			}
		}
	}
}

int main() 
{
	int i, j;
	int from, to, length;
	while (scanf("%d%d", &n, &m) && n) 
	{
		for (i=0; i<NUM; i++)
			for (j=1; j<NUM; j++)
				a[i][j] = NoEdge;
		for (i=0; i<m; i++)
		{
			scanf("%d%d%d", &from, &to, &length);
			a[from][to] = length;
			a[to][from] = length;
		}
		bestc = NoEdge;
		for(i=1; i<=n; i++)
			x[i] = i;
		Backtrack(2);
		for(j=1; j<=n; j++)
			printf("%d ", bestx[j]);
		printf("\n%d\n", bestc);
	}	
	return 0;
}