目录
二叉树遍历
先序遍历
递归
/**
* 先序遍历
*
* 这三种不同的遍历结构都是一样的,只是先后顺序不一样而已
*
* @param node
* 遍历的节点
*/
public static void preOrderTraverse(Node node) {
if (node == null)
return;
System.out.print(node.data + " ");
preOrderTraverse(node.leftChild);
preOrderTraverse(node.rightChild);
} 非递归
法1
public List<Integer> preorderTraversal(TreeNode root) {
ArrayList<Integer> list = new ArrayList<Integer>();
Stack<TreeNode> stk = new Stack<>();
stk.push(root);
while(!stk.isEmpty()){
TreeNode node = stk.pop();
if(node==null)
continue;
list.add(node.val);
stk.push(node.right);
stk.push(node.left);
}
return list;
}
法2!!!
private void preOrder2(BiTNode node) {
Stack<BiTNode> stack = new Stack<BiTNode>();
while(node!=null||!stack.isEmpty()) {
while(node!=null) {
System.out.print(node.data);
stack.push(node);
node=node.lchild;
}
node=stack.pop().rchild;
}
}中序遍历
递归
/**
* 中序遍历
*
* 这三种不同的遍历结构都是一样的,只是先后顺序不一样而已
*
* @param node
* 遍历的节点
*/
public static void inOrderTraverse(Node node) {
if (node == null)
return;
inOrderTraverse(node.leftChild);
System.out.print(node.data + " ");
inOrderTraverse(node.rightChild);
} 非递归
private void inOrder2(BiTNode node) {
Stack<BiTNode> stack = new Stack<BiTNode>();
while(node!=null||!stack.isEmpty()) {
while(node!=null) {
stack.push(node);
node=node.lchild;
}
node=stack.pop();
System.out.print(node.data);
node=node.rchild;
}
}
后序遍历
递归
/**
* 后序遍历
*
* 这三种不同的遍历结构都是一样的,只是先后顺序不一样而已
*
* @param node
* 遍历的节点
*/
public static void postOrderTraverse(Node node) {
if (node == null)
return;
postOrderTraverse(node.leftChild);
postOrderTraverse(node.rightChild);
System.out.print(node.data + " ");
} 非递归
/**
* 后序遍历
*/
public List<Integer> postorderTraversal(TreeNode root) {
LinkedList<Integer> list = new LinkedList<Integer>();
Stack<TreeNode> stk = new Stack<>();
stk.push(root);
while(!stk.isEmpty()){
TreeNode node = stk.pop();
if(node==null)
continue;
list.addFirst(node.val); //LinkedList's method. If using ArrayList here,then using 'Collections.reverse(list)'' in the end;
stk.push(node.left);
stk.push(node.right);
}
return list;
}层序遍历
public static void levelTraversal(TreeNode root){
if(root == null) {
return;
}
Queue<TreeNode> queue = new LinkedList<>(); // 对列保存树节点
queue.add(root);
while (!queue.isEmpty()) {
TreeNode temp = queue.poll();
System.out.print(temp.val + "->");
if (temp.left != null) { // 添加左右子节点到对列
queue.add(temp.left);
}
if (temp.right != null) {
queue.add(temp.right);
}
}数组生成树
法·1
import java.util.LinkedList;
import java.util.List;
public class BinTreeTraverse2 {
private int[] array = { 1, 2, 3, 4, 5, 6, 7, 8, 9 };
private static List<Node> nodeList = null;
private static class Node {
Node leftChild;
Node rightChild;
int data;
Node(int newData) {
leftChild = null;
rightChild = null;
data = newData;
}
}
public void createBinTree() {
nodeList = new LinkedList<Node>();
// 将一个数组的值依次转换为Node节点
for (int nodeIndex = 0; nodeIndex < array.length; nodeIndex++) {
nodeList.add(new Node(array[nodeIndex]));
}
// 对前lastParentIndex-1个父节点按照父节点与孩子节点的数字关系建立二叉树
for (int parentIndex = 0; parentIndex < array.length / 2 - 1; parentIndex++) {
// 左孩子
nodeList.get(parentIndex).leftChild = nodeList
.get(parentIndex * 2 + 1);
// 右孩子
nodeList.get(parentIndex).rightChild = nodeList
.get(parentIndex * 2 + 2);
}
// 最后一个父节点:因为最后一个父节点可能没有右孩子,所以单独拿出来处理
int lastParentIndex = array.length / 2 - 1;
// 左孩子
nodeList.get(lastParentIndex).leftChild = nodeList
.get(lastParentIndex * 2 + 1);
// 右孩子,如果数组的长度为奇数才建立右孩子
if (array.length % 2 == 1) {
nodeList.get(lastParentIndex).rightChild = nodeList
.get(lastParentIndex * 2 + 2);
}
}
法2
public class binTree {
public static void main(String[] args) {
Integer[] a = {3,9,20,null,null,15,7,null,null,null,null};
int i=1;
BinNode root = new BinNode(a[0]); // 根节点
BinNode current = null;
Integer value = null;
//层序创建二叉树
LinkedList<BinNode> queue = new LinkedList<BinNode>();
queue.offer(root);
while(i<a.length) {
current = queue.poll();//从链表中移除并获取第一个节点
value = a[i++];
if(value!=null) {
BinNode left =new BinNode(value);
current.setLeftNode(left);//创建当前节点的左孩子
queue.offer(left); // 在链表尾部 左孩子入队
}
value=a[i++];
if(value!=null) {
BinNode right =new BinNode(value);
current.setRightNode(right);//创建当前节点的右孩子
queue.offer(right);// 在链表尾部 右孩子入队
}
}
levelIetrator(root);
}层序创建树
public class binTree {
public static void main(String[] args) {
Integer[] a = {3,9,20,null,null,15,7,null,null,null,null};
int i=1;
BinNode root = new BinNode(a[0]); // 根节点
BinNode current = null;
Integer value = null;
//层序创建二叉树
LinkedList<BinNode> queue = new LinkedList<BinNode>();
queue.offer(root);
while(i<a.length) {
current = queue.poll();//从链表中移除并获取第一个节点
value = a[i++];
if(value!=null) {
BinNode left =new BinNode(value);
current.setLeftNode(left);//创建当前节点的左孩子
queue.offer(left); // 在链表尾部 左孩子入队
}
value=a[i++];
if(value!=null) {
BinNode right =new BinNode(value);
current.setRightNode(right);//创建当前节点的右孩子
queue.offer(right);// 在链表尾部 右孩子入队
}
}
levelIetrator(root);
}
获取树深度
递归
public int maxDepth(TreeNode root) {
int d = 0;
if (root == null) {
return 0;
}
d = Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
return d;
}
非递归
利用层序遍历的思想
public static int getDepth(TreeNode root) {
if (root == null) {
return 0;
}
int currentLevelCount = 1; // 当前层的节点数量
int nextLevelCount = 0; // 下一层节点数量
int depth = 0; // 树的深度
Queue<TreeNode> queue = new LinkedList<>(); // 对列保存树节点
queue.add(root);
while (!queue.isEmpty()) {
TreeNode temp = queue.remove(); // 移除节点
currentLevelCount--; // 当前层节点数减1
if (temp.left != null) { // 添加左节点并更新下一层节点个数
queue.add(temp.left);
nextLevelCount++;
}
if (temp.right != null) { // 添加右节点并更新下一层节点个数
queue.add(temp.right);
nextLevelCount++;
}
if (currentLevelCount == 0) { // 如果是该层的最后一个节点,树的深度加1
depth++;
currentLevelCount = nextLevelCount; // 更新当前层节点数量并且重置下一层节点数量
nextLevelCount = 0;
}
}
return depth;
}求二叉树第k层的节点个数
public static int getNodeNumKthLevelRec(TreeNode root, int k) {
if (root == null || k < 1) {
return 0;
}
if (k == 1) {
return 1;
}
return getNodeNumKthLevelRec(root.left, k - 1) + getNodeNumKthLevelRec(root.right, k - 1);
}求二叉树中叶子节点的个数
递归
public static int getNodeNumLeafRec(TreeNode root) {
if (root == null) {
return 0;
}
if (root.left == null && root.right == null) {
return 1;
}
return getNodeNumLeafRec(root.left) + getNodeNumLeafRec(root.right);
}非递归
基于层序遍历
public static int getNodeNumLeafRec(TreeNode root) {
if (root == null) {
return 0;
}
if (root.left == null && root.right == null) {
return 1;
}
return getNodeNumLeafRec(root.left) + getNodeNumLeafRec(root.right);
}
判断两棵二叉树是否相同的树
递归
public static boolean isSameRec(TreeNode r1, TreeNode r2) {
if (r1 == null && r2 == null) { // 都是空
return true;
} else if (r1 == null || r2 == null) { // 有一个为空,一个不为空
return false;
}
if (r1.val != r2.val) { // 两个不为空,但是值不相同
return false;
}
return isSameRec(r1.left, r2.left) && isSameRec(r1.right, r2.right); // 递归遍历左右子节点
}非递归
public static boolean isSame(TreeNode r1, TreeNode r2){
if (r1 == null && r2 == null) { // 都是空
return true;
} else if (r1 == null || r2 == null) { // 有一个为空,一个不为空
return false;
}
Stack<TreeNode> stack1 = new Stack<>();
Stack<TreeNode> stack2 = new Stack<>();
stack1.add(r1);
stack2.add(r2);
while (!stack1.isEmpty() && !stack2.isEmpty()) {
TreeNode temp1 = stack1.pop();
TreeNode temp2 = stack2.pop();
if (temp1 == null && temp2 == null) { // 两个元素都为空,因为添加的时候没有对空节点做判断
continue;
} else if (temp1 != null && temp2 != null && temp1.val == temp2.val) {
stack1.push(temp1.left); // 相等则添加左右子节点判断
stack1.push(temp1.right);
stack2.push(temp2.left);
stack2.push(temp2.right);
} else {
return false;
}
}
return true;
}判断二叉树是不是平衡二叉树
public static boolean isAVLTree(TreeNode root) {
if (root == null) {
return true;
}
if (Math.abs(getDepth(root.left) - getDepth(root.right)) > 1) { // 左右子树高度差大于1
return false;
}
return isAVLTree(root.left) && isAVLTree(root.right); // 递归判断左右子树
}二叉树的镜像
1.破坏原树
public static TreeNode mirrorRec(TreeNode root) {
if (root == null) {
return root;
}
TreeNode left = mirrorRec(root.right); // 递归镜像左右子树
TreeNode right = mirrorRec(root.left);
root.left = left; // 更新根节点的左右子树为镜像后的树
root.right = right;
return root;
}
2.不破坏原树
public static TreeNode mirrorCopyRec(TreeNode root) {
if (root == null) {
return root;
}
TreeNode newRoot = new TreeNode(root.val); // 创建新节点,然后交换左右子树
newRoot.left = mirrorCopyRec(root.right);
newRoot.right = mirrorCopyRec(root.left);
return newRoot;
}判断是否为二分查找树BST
递归解法:中序遍历的结果应该是递增的
根据前序中序遍历结果重建二叉树
public static BinaryTreeNode ConstructCore(int[] preOrder,int startPreIndex, int endPreIndex,
int[] inOrder,int startInIndex, int endInIndex) throws InvalidPutException {
int rootValue = preOrder[startPreIndex];
System.out.println("rootValue = " + rootValue);
BinaryTreeNode root = new BinaryTreeNode(rootValue);
// 只有一个元素
if (startPreIndex == endPreIndex) {
if (startInIndex == endInIndex
&& preOrder[startPreIndex] == inOrder[startInIndex]) {
System.out.println("only one element");
return root;
} else {
throw new InvalidPutException();
}
}
// 在中序遍历中找到根结点的索引
int rootInIndex = startInIndex;
while (rootInIndex <= endInIndex && inOrder[rootInIndex] != rootValue) {
++rootInIndex;
}
if (rootInIndex == endInIndex && inOrder[rootInIndex] != rootValue) {
throw new InvalidPutException();
}
int leftLength = rootInIndex - startInIndex;
int leftPreOrderEndIndex = startPreIndex + leftLength;
if (leftLength > 0) {
// 构建左子树
root.leftNode = ConstructCore(preOrder, startPreIndex + 1,
leftPreOrderEndIndex, inOrder, startInIndex,
rootInIndex - 1);
}
if (leftLength < endPreIndex - startPreIndex) {
// 右子树有元素,构建右子树
root.rightNode = ConstructCore(preOrder, leftPreOrderEndIndex + 1,
endPreIndex, inOrder, rootInIndex + 1, endInIndex);
}
return root;
}树的子结构
查找A中是否存在树B结构一样的子树,可以分为两步:
第一步,在树A中找到和树B的根节点的值一样的节点R(层序遍历)
第二步,判断A中以R为根节点的子树是不是包含和树B一样的结构(判断两棵二叉树是否相同的树)
以上面为例,先在A中找到值为8的节点,接着判断树A的根节点下面的子树是不是含有和树B一样的结构。在A中根节点的左子节点为8,而树B的根节点的左子节点为9,对应两个节点不同。
接着找8的节点,在A中第二层找到,然后进行第二步的判断(判断这个节点下面的子树是否含有树B一样的结构)
二叉树中和为某一值的路径
public void findPath(BinaryTreeNode root, int expectedSum, Stack<Integer> stack, int currentSum) {
stack.push(root.value);
currentSum += root.value;
boolean isLeaf = (root.left == null) && (root.right == null);
//如果该节点为叶子节点,并且路径和等于expectedSum
if(currentSum == expectedSum && isLeaf){
// 打印路径
printStack(stack);
}
//如果不是叶节点,则遍历它的子节点
if(root.left != null){
findPath(root.left, expectedSum, stack, currentSum);
}
if(root.right != null){
findPath(root.right, expectedSum, stack, currentSum);
}
//在返回父节点之前,在路径上删除当前节点
stack.pop();
currentSum -= root.value;
}序列化二叉树
利用层序遍历
public class Serialize {
String Serialize(TreeNode root) {
if(root == null){
return null;
}
StringBuffer sb = new StringBuffer();
ArrayList<TreeNode> list = new ArrayList<TreeNode>();
int count = (1 << treeDepth(root)) - 1;//计数,拿到此树的深度后计算对应完全二叉树节点数
list.add(root);
count--;
TreeNode tmpNode = null;
//层次遍历二叉树,开始序列化
while(list.size() > 0 && count >= 0){
tmpNode = list.remove(0);
if(tmpNode != null){
sb.append(tmpNode.val+",");
list.add(tmpNode.left);
list.add(tmpNode.right);
}else{
sb.append("#,");//#作为空节点占位符
list.add(null);
list.add(null);
}
count --;
}
return sb.toString();
}
TreeNode Deserialize(String str) {
if(str == null || str.length() == 0){
return null;
}
return Deserialize(str.split(","), 0);
}
TreeNode Deserialize(String[] strings, int index){
TreeNode newNode = null;
if(index < strings.length){
if(!strings[index].equals("#")){
newNode = new TreeNode(Integer.parseInt(strings[index]));
newNode.left = Deserialize(strings, 2 * index + 1);
newNode.right = Deserialize(strings, 2 * index + 2);
}
}
return newNode;
}
int treeDepth(TreeNode root){
int depth = 0;
if(root == null){
return depth;
}else{
int lDepth = treeDepth(root.left) + 1;
int rDepth = treeDepth(root.right) + 1;
return lDepth > rDepth ? lDepth : rDepth;
}
}
}第K大节点
public class E54KthBSTNode {
//二叉搜索树中第k个节点
private static int index;
public static BinaryTreeNode getKthNode(BinaryTreeNode root, int k){
if (root == null)
return null;
index = k;
return getKthNodeCore(root);
}
private static BinaryTreeNode getKthNodeCore(BinaryTreeNode root) {
//采用二叉树的中序遍历顺序查找第k个节点
BinaryTreeNode target = null;
if (root.left != null)
target = getKthNodeCore(root.left);
if (target == null){
if (index == 1)
target = root;
index--;
}
if (target == null && root.right != null)
target = getKthNodeCore(root.right);
return target;
}
}B树定义
B树和平衡二叉树稍有不同的是B树属于多叉树又名平衡多路查找树(查找路径不只两个),不属于二叉搜索树的范畴,因为它不止两路,存在多路。

B树满足的条件:
(1)树种的每个节点最多拥有m个子节点且m>=2,空树除外(注:m阶代表一个树节点最多有多少个查找路径,m阶=m路,当m=2则是2叉树,m=3则是3叉);
(2)除根节点外每个节点的关键字数量大于等于ceil(m/2)-1个小于等于m-1个,非根节点关键字数必须>=2;(注:ceil()是个朝正无穷方向取整的函数 如ceil(1.1)结果为2)
(3)所有叶子节点均在同一层、叶子节点除了包含了关键字和关键字记录的指针外也有指向其子节点的指针只不过其指针地址都为null对应下图最后一层节点的空格子
(4)如果一个非叶节点有N个子节点,则该节点的关键字数等于N-1;
(5)所有节点关键字是按递增次序排列,并遵循左小右大原则;
B树的应用场景:
构造一个多阶的B类树,然后在尽量多的在结点上存储相关的信息,保证层数尽量的少,以便后面我们可以更快的找到信息,磁盘的I/O操作也少一些,而且B类树是平衡树,每个结点到叶子结点的高度都是相同,这也保证了每个查询是稳定的。
————————————————
版权声明:本文为CSDN博主「祚儿疯」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/u012414189/article/details/83832161
B+树
B+树是B树的一个升级版,B+树是B树的变种树,有n棵子树的节点中含有n个关键字,每个关键字不保存数据,只用来索引,数据都保存在叶子节点。是为文件系统而生的。

相对于B树来说B+树更充分的利用了节点的空间,让查询速度更加稳定,其速度完全接近于二分法查找。为什么说B+树查找的效率要比B树更高、更稳定;
我们先看看B和B+树两者的区别
(1)B+跟B树不同,B+树的非叶子节点不保存关键字记录的指针,这样使得B+树每个节点所能保存的关键字大大增加;
(2)B+树叶子节点保存了父节点的所有关键字和关键字记录的指针,每个叶子节点的关键字从小到大链接;
(3)B+树的根节点关键字数量和其子节点个数相等;
(4)B+的非叶子节点只进行数据索引,不会存实际的关键字记录的指针,所有数据地址必须要到叶子节点才能获取到,所以每次数据查询的次数都一样;
B+树特点:
在B树的基础上每个节点存储的关键字数更多,树的层级更少所以查询数据更快,所有指关键字指针都存在叶子节点,所以每次查找的次数都相同所以查询速度更稳定;
应用场景:
用在磁盘文件组织 数据索引和数据库索引。
————————————————
版权声明:本文为CSDN博主「祚儿疯」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/u012414189/article/details/83832161
Trie树(字典树)
trie,又称前缀树,是一种有序树,用于保存关联数组,其中的键通常是字符串。与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
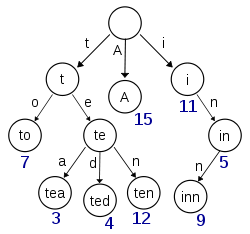
在图示中,键标注在节点中,值标注在节点之下。每一个完整的英文单词对应一个特定的整数。Trie 可以看作是一个确定有限状态自动机,尽管边上的符号一般是隐含在分支的顺序中的。
键不需要被显式地保存在节点中。图示中标注出完整的单词,只是为了演示 trie 的原理。
trie树的优点:
利用字符串的公共前缀来节约存储空间,最大限度地减少无谓的字符串比较,查询效率比哈希表高。
trie树的缺点:
Trie树是一种比较简单的数据结构.理解起来比较简单,正所谓简单的东西也得付出代价.故Trie树也有它的缺点,Trie树的内存消耗非常大.
其基本性质可以归纳为:
根节点不包含字符,除根节点外每一个节点都只包含一个字符。
从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
每个节点的所有子节点包含的字符都不相同。
典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。字典树与字典很相似,当你要查一个单词是不是在字典树中,首先看单词的第一个字母是不是在字典的第一层,如果不在,说明字典树里没有该单词,如果在就在该字母的孩子节点里找是不是有单词的第二个字母,没有说明没有该单词,有的话用同样的方法继续查找.字典树不仅可以用来储存字母,也可以储存数字等其它数据。
————————————————
版权声明:本文为CSDN博主「祚儿疯」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/u012414189/article/details/83832161
树的应用
红黑树:
STL中set、multiset、map、multimap底层是红黑树实现的
trie树:
统计,排序和保存大量的字符串
B/B+树:
在尽量多的在结点上存储相关的信息,用在磁盘文件组织 数据索引和数据库索引