骑士游历问题【JAVA板】代码详细流

先说明一下算法问题，在棋盘上，要怎么选择行走的方向才能遍历整个棋盘呢。简单来说，就是选择一个在选择了它之后它的下一步可选方向最少的那一个方向。总体上就是先选择比较困难的路来走，将比较简单的路线留到后面再走。
那么接下来我们先来看看一个8x8的棋盘上每个格子的可走方向来理解一下这个算法。
先上代码。（注意！下面这个代码不是用来解决骑士游历问题的）

`public class Bushu {
	 private  boolean ac(int[][] board) {
	int[] movex = { -2, -1, 1, 2,  2,  1, -1, -2 };
    int[] movey = {  1,  2, 2, 1, -1, -2, -2, -1 };
int i = 0;
int j = 0;
int temJ = 0;
int temI=0;
for(i=0;i<board.length;i++)
		{for(j=0;j<board.length;j++) {
		int count=0;
for(int k=0;k<=7;k++)
{temI			=i+movex[k];
temJ		    =j+movey[k];
		
if (temI < 0 || temI > 7 || temJ < 0 || temJ > 7) {
	        continue;
	    }
		else {
 
        count++;
        board[i][j]=count;}
    }
	}
	}
return true;
 }
 public static void main(String[] args) {
        int[][] board = new int[8][8];
        Bushu aaa = new Bushu();
        if (aaa.ac(board)) {
            System.out.println("完成：");
        }
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                if (board[i][j] < 10) {
                    System.out.print(" " + board[i][j]);
                } else {
                    System.out.print(board[i][j]);
                }
                System.out.print(" ");
            }
            System.out.println();
        }
 }

}`

经过运算，可以得到以下结果

完成：
 2  3  4  4  4  4  3  2 
 3  4  6  6  6  6  4  3 
 4  6  8  8  8  8  6  4 
 4  6  8  8  8  8  6  4 
 4  6  8  8  8  8  6  4 
 4  6  8  8  8  8  6  4 
 3  4  6  6  6  6  4  3 
 2  3  4  4  4  4  3  2 

所以最后骑士的游历顺序会大体上沿着棋盘边缘那些可选择方向少的格子去遍历然后渐渐向中心靠近。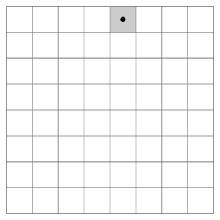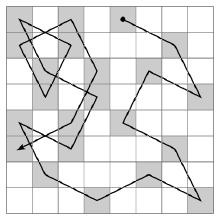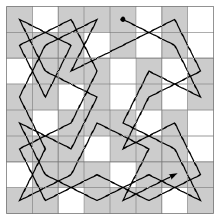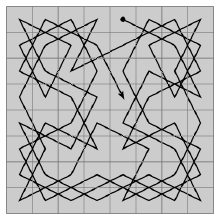（图片来自互联网）

接下来就是我们的正式代码了（代码来自互联网，博主对代码进行了一些修进同时加了注释方便理解）

import java.util.*;
public class Knight {

private boolean Travel(int firstX, int firstY, int[][] board) {
	//int[][] board = new int[8][8]
    // x，y分别对应骑士可走的8个方向
    int[] movex = { -2, -1, 1, 2,  2,  1, -1, -2 };
    int[] movey = {  1,  2, 2, 1, -1, -2, -2, -1 };

    // 用于记录下一步可以移动的各个位置
    int[] nextStepX = new int[board.length];
    int[] nextStepY = new int[board.length];

    // exitS记录出路的个数
    int[] exitS = new int[board.length];
    //nextX,nextY用于存放实际移动方向
    int nextX = firstX;
    int nextY = firstY;
    //第一个位置由用户设定，并且在数组中赋值为1
    board[nextX][nextY] = 1;

    for (int m = 2; m <= Math.pow(board.length, 2); m++) {
        //math.pow(a,b)用于计算a的b次方
        //初始化下一个位置可走的位置的数目
        for (int i = 0; i < board.length; i++) {
            exitS[i] = 0;
        }
        //count用来记录下一步移动可以有多少个方向的选择
        int count = 0;
        // 试探8个方向
        for (int i = 0; i < 8; i++) {
            int temI = nextX + movex[i];//:18,19
            int temJ = nextY + movey[i];
            // 走到边界，路断
            if (temI < 0 || temI > 7 || temJ < 0 || temJ > 7) {
                continue;
            }

            // 记录下可走的方向
            if (0 == board[temI][temJ]) {
                nextStepX[count] = temI;//这里的nextStepX和nextStepY已经存储了可行方向的坐标了:33,34
                nextStepY[count] = temJ;
                count++;
            }
        }

        // 到这里，cout表示当前点有几种走法。nextStep中存储各种走法的坐标。
        //min用来存放选择哪个方向的数字
        int min = -1;
        if (count == 0) {
           return false;
        }

        if (1 == count) {
            min = 0;
        } else {// 这一步是为了找到下一次走法中最少种走法的那一步
            for (int i = 0; i < count; i++) {
                for (int j = 0; j < 8; j++) {//这里的nextStepX和nextStepY已经存放了下一步的移动方向:42
                    int temI = nextStepX[i] + movex[j];//再次加上movex和movey来测定下一步走法中最少方向选择项
                    int temJ = nextStepY[i] + movey[j];
                    if (temI < 0 || temI > 7 || temJ < 0 || temJ > 7) {
                        continue;
                    }
                    
                    // 记录下这个位置可走的方向数
                    if (0 == board[temI][temJ]) {
                        exitS[i]++;
                    }
                }
            }

            int tem = exitS[0];
            min = 0;

            // 从可走的方向中，寻找最少走的出路
            for (int i = 1; i < count; i++) {
                if (tem > exitS[i]) {
                    tem = exitS[i];
                    min = i;
                }
            }
        }

        // 得到最少的出路
        nextX = nextStepX[min];
        nextY = nextStepY[min];
        board[nextX][nextY] = m;
    }

    return true;
}

public static void main(String[] args) {

    int firstX, firstY;
    System.out.println("输入起始点(0-7)：");
    Scanner scanner = new Scanner(System.in);

    firstX = scanner.nextInt();
    firstY = scanner.nextInt();
    int[][] board = new int[8][8];
    Knight knight = new Knight();

    if (knight.Travel(firstX, firstY, board)) {
        System.out.println("游历完成：");
    } else {
        System.out.println("游历失败！\n");
    }

    for (int i = 0; i < board.length; i++) {
        for (int j = 0; j < board[0].length; j++) {
            if (board[i][j] < 10) {
                System.out.print(" " + board[i][j]);
            } else {
                System.out.print(board[i][j]);
            }
            System.out.print(" ");
        }
        System.out.println();
     }
    }
}

那么当我们在开发平台上运行一下这个程序:

输入起始点(0-7)：
1
1
游历完成：
63 54 15  2 27 38 17  4 
14  1 64 55 16  3 28 37 
53 62 13 26 39 56  5 18 
12 25 58 61 46 41 36 29 
59 52 45 40 57 48 19  6 
24 11 60 47 42 35 30 33 
51 44  9 22 49 32  7 20 
10 23 50 43  8 21 34 31 

这样就完成了哦！

作者：何庆涛clack.