利用先、中、后序遍历顺序重构二叉树

说明：

以先序遍历和中序遍历为例。因为先序和后续遍历是反过来的，所以处理类似。至于使用先序和后序遍历重构，有待发现咯▲嘻嘻▲

题目

给定一个二叉树的先序遍历顺序和一个中序遍历顺序(一种遍历中不含存在重复数据)，希望你能重构该二叉树？

构建节点的数据结构：

class TreeNode{
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode(int x) { val = x; }
}

例：

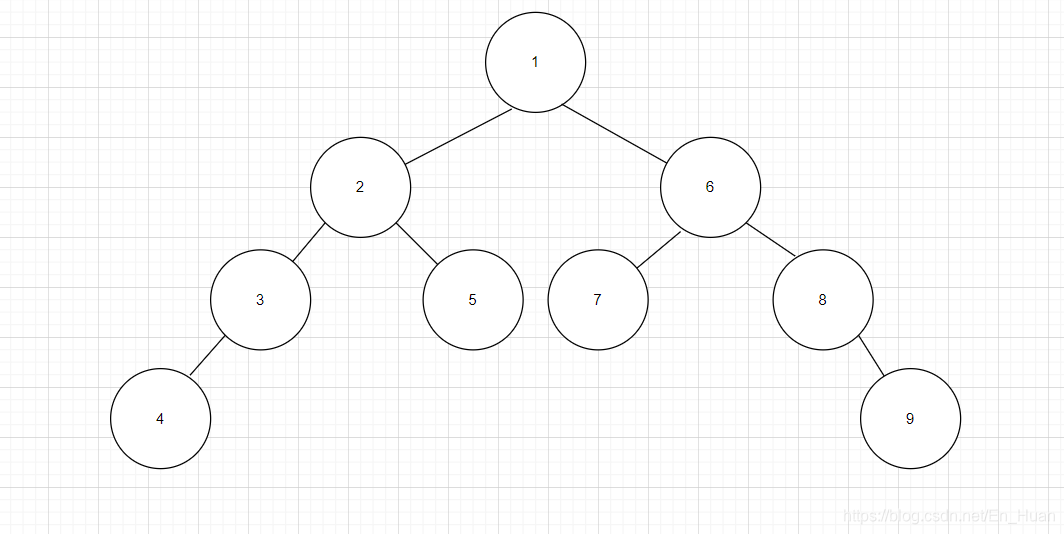
     先序遍历：preorder = [1,2,3,4,5,6,7,8,9]

     中序遍历：inorder   = [4,3,2,5,1,7,6,8,9]

思路

 若能直接按照先序遍历或者中序顺序重构二叉树无疑是最好的选择。

 若选用先序遍历建立二叉树，我们遇到的问题是，该何时从构建左子树的过程中结束（我们称该节点为一个结束点）？

 如：使用先序遍历1,2,3,4到了4的时候我们就应该结束当前子树的构建（第一个结束点）。

此时发现4这个结束点在中序遍历中刚好是第一个出现的，此时也是我们遍历时出现的第一个结束点。

检查正确的先序遍历过程中其他结束点我们发现：

   先序遍历中结束点出现的顺序就是中序遍历的顺序，那么我们可以从先序遍历构建二叉树的过程中改进一下，增加一个判断当前是否是结束点的条件（即当前遍历节点的值是否与中序遍历中的值相同）,若当前点是结束点，则结束当前子树的遍历。

程序

class TreeNode{
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode(int x) { val = x; }
}

public class BuildTree {
    private int nowPreIndex;
    private int nowInIndex;
    private int preLength;
    int [] preorder,inorder;

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder==null||inorder==null)
            return null;
        nowPreIndex = nowInIndex =0;
        this.preLength = preorder.length;
        this.preorder = preorder;
        this.inorder = inorder;
        //函数递归顺序同先序遍历,此时函数执行从最内层到的顺序与inorder中的顺序相同
        return buildTree2(Integer.MAX_VALUE);
    }
    private TreeNode buildTree2(int inStop){
        if(nowPreIndex>=preLength) //到达先序遍历最后一个元素
            return null;
        if(inorder[nowInIndex] == inStop){ //中序遍历和先序遍历相遇则为真,左子树完毕，返回上一层
            ++ nowInIndex; //中序遍历下一个
            return null;
        }
        TreeNode node = new TreeNode(preorder[nowPreIndex++]);  //
        node.left = buildTree2(node.val); //构造左子树
        node.right = buildTree2(inStop);  //构造右子树
        return node;
    }
}