F. Tokitsukaze and Permutations

题意：
给你长度为$n(n\le 10^6)$的排列，可以进行$k(k<n)$次操作，每次操作从$1$遍历到$n$，如果$a_i>a_{i+1}$，则交换两个数字。
给你数组$v(v_i<i)$，$v_i$表示$a_1\sim a_{i-1}$中小于$a_i$的数字的数量
，如果$v_i=-1$,说明这个地方的结果丢失，可以是任意的值，问有多少种可能的排列，在$k$次交换后，可以得到数组$v$，答案对$998244353$取模。
思路：
首先，对于任意一种构造的$v$，只要能够满足$v_i<i$，都有且只有一种排列能与之对应。
也就是说，只要我们能够任意构造出来不同的$v$，就会有与之对应的排列能够匹配，那么这样的构造有$n!$种，但是其中有没有不合法的情况呢？
观察这种操作发现这个操作其实是冒泡排序中的一个回合，在操作完$k$个回合后，可以保证最后的$k$个数字一定已经按序归位，且是排列中最大的$k$个数字，在这种情况下$v_{n-k+1}\sim v_n$的值只能是$0$，所以刚才的构造不够合理。
只要有$v_{n-k+1}\sim v_n$的值不为$0$或$-1$，此序列一定无解。

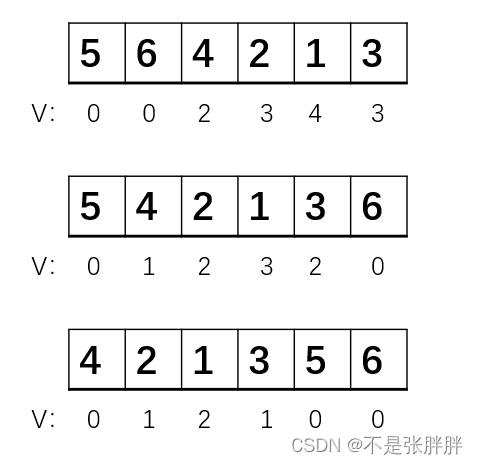
此外还可以发现，每次操作一次，都会使所有的$v_i=max(0,v_i-1)$，然后左移一格，将第一格直接覆盖掉，将$v_n=0$
考虑每个格子有多少种情况，总乘积就是我们的答案
操作$k$次，就会直接覆盖掉前$k$格，所以前$k$格不管填什么都没有影响，贡献是$k!$
接下来是后面的格子，定义$V$为排列的$v$，$v_i=max(V_{i+k}-k,0)$
若$v_i$大于$0$，则我们确定$V_{i+k}=v_i+k$结果唯一
若$v_i=0$，则$V_{i+k}$可以是$0\sim k$贡献为$k+1$
若$v_i=-1$，无法判断，我们只要让$v_i<i$即可，贡献为$i$

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e6+7;
int a[maxn];
ll mod=998244353;
int main()
{
	int T;
	scanf("%d",&T);
	while(T--)
	{
		int n,k;scanf("%d%d",&n,&k);
		int ok=1;
		for(int i=1;i<=n;i++)
		{
			scanf("%d",&a[i]);
			if(i>=n-k+1 && a[i]>0) ok=0;
		}
		if(!ok)
		{
			puts("0");continue;
		}
		ll ans=1;
		for(int i=k+1;i<=n;i++)
		{
			if(a[i-k]==0) ans=(ans*(k+1))%mod;
			else if(a[i-k]==-1) ans=(ans*i)%mod;
		}
		for(int i=1;i<=k;i++) ans*=i,ans%=mod;
		printf("%lld\n",ans);
	}
}