外部排序
文章目录:
- 外部排序的概念
- 外部排序的流程分析(涉及到三个子算法)
- 时间复杂度和空间复杂度问题
1.什么是外部排序



2.外部排序的流程分析
一.得到初始化归并段
1.划分记录段(为了得到初始化归并段)
这里用到了置换-选择排序作为子算法来实现这一过程(下面是此算法的核心)
2.从读入内存的这组记录中选出最小的值(并写回外存)
3.将其所在记录段的次小值读入内存以补上空位置,将所有组的记录全部导出外存时得到了初始化归并段,之后进行归并操作。(可以用归并排序的算法进行排序)
二.优化归并过程
这里用到两个子算法来对归并过程进行优化
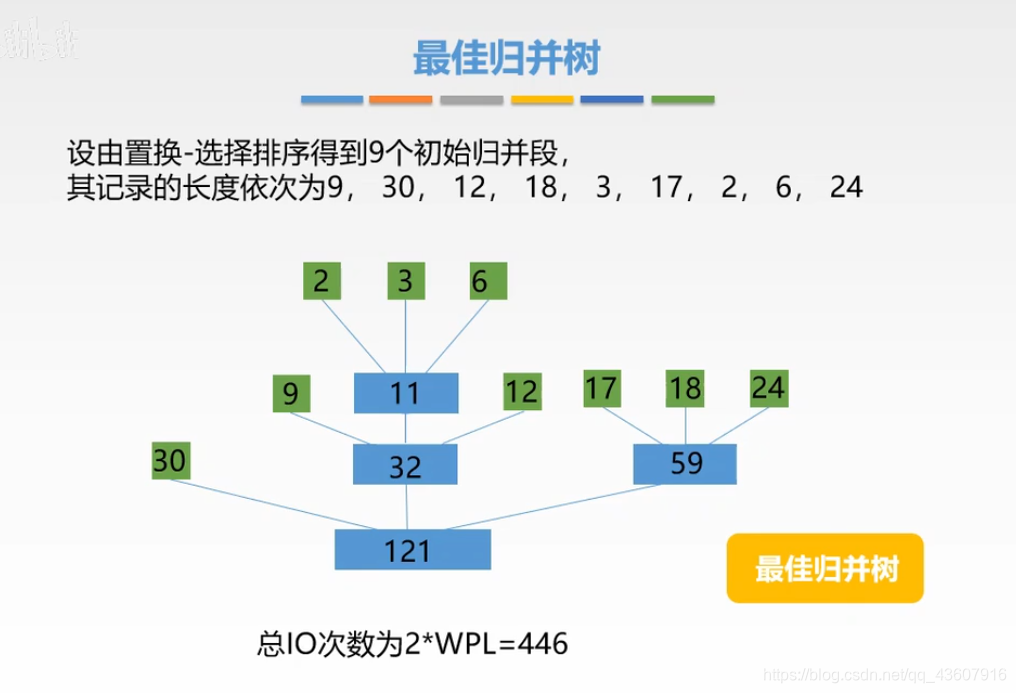
1)最佳归并树
优化什么?:由上述置换-选择排序构造初始化归并段可知,通过此算法得到的初始归并段长度可能是不同的,所以不同的归并策略可能导致归并次数的不同,所以,这个算法是用来优化归并次数的,使得归并次数最少,(进而提高效率)。
注意:构造最佳归并树,对于k路归并算法,可以通过构造k叉赫夫曼树来 构造最佳归并树(通过赫夫曼树来优化归并树的带权路径长度)
下面的几点是需要知道和掌握的具体的小知识点:
- I/O次数=带权路径长度*2;(2是入是一次,出是一次所以两 次,要乘以2)
- 每个记录每次归并都有两次I/O操作
2)败者树
优化什么?:在k路归并中,如果不使用败者树,则每次归并对于读入的值都需进行k-1次比较才能得到最值,所以,这个算法是用来优化选最值这一步的比较次数的,使比较次数最少选出最值
上述过程组成了k路归并排序,也是k路归并排序的核心。
这里置换-选择排序,最佳归并树,和败者树的详细过程要掌握
 (跟胜利者比较)
(跟胜利者比较)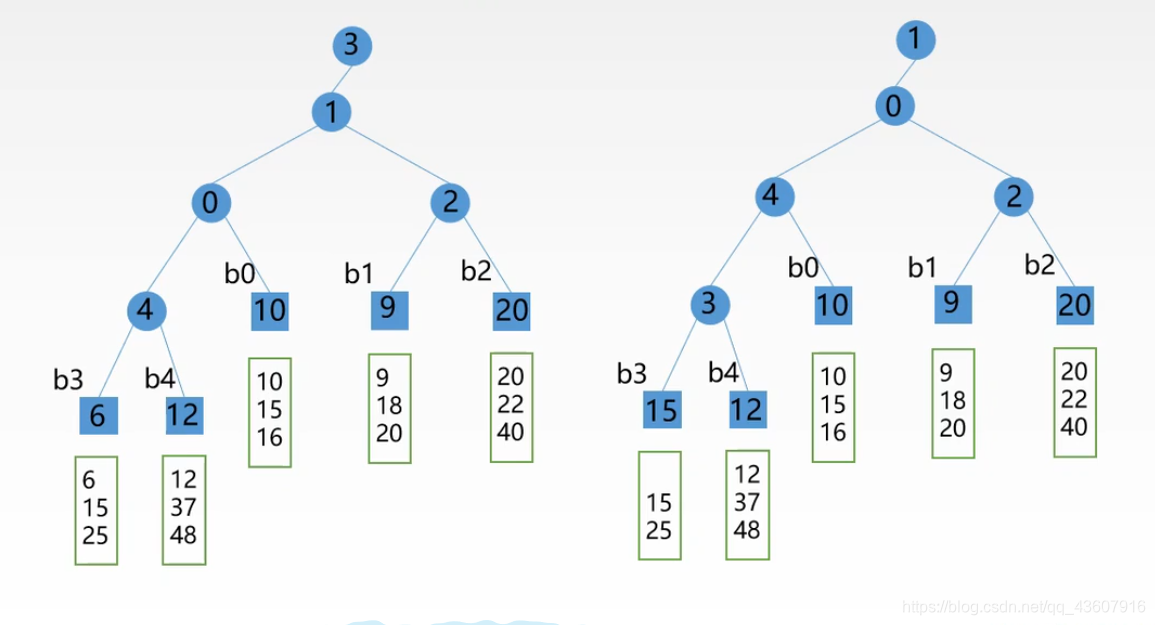





3.时间复杂度和空间复杂度
需要掌握以下几点:
- m个初始归并段进行k路归并,归并的趟数为logk底m取上限。
每次归并,所有记录都要进行两次I/O操作。 - k路归并的败者树高度为[log2底k]+1,其时间复杂度为O(log2底k)
- k路归并败者树的建树时间复杂度为O(klog2底k)。
- 空间复杂度为O(1)。
- 通过对树结构的局部调整,来恢复树的结构,无须重新建树,局部恢复即可恢复结构,从而降低时间复杂度,这就是选择树的思想。
到这里所有排序的基本知识都整理完成,之后会更新数组矩阵广义表章节和树的章节。
2020.8.12.
版权声明:本文为qq_43607916原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。